树的直径

前言

那年，CCF把CSP-S办成了植树节...

为了准备以后的植树节，教练也在机房让大家种树..

---

最近一直在接触树上知识，先来讲讲树的直径绝对不是因为只搞懂了这个

树的直径，即在一棵树中，最远的两个节点之间的距离，也可以指这条路径。下面树的直径都指的是它的距离长度。

Tree dp或是两次搜索的时间复杂度都是\(O(n)\)，不会树形dp所以不写

---

思路

大致思路是这样的，从根节点(任意一个点都可以)P出发，一次搜索找到离这个点距离最远的点Q，再从点Q出发再次搜索，搜到离Q最远的点W，这样两次搜索到的两个节点Q,W就是直径的两个端点。这样的方法代码量略大，但是可以比较方便地(指与Tree dp比较)记录路径。

---

证明

怎么证明这种方法找到的就是树的直径呢？

这里需要分类讨论。

1.P在直径上。

根据树的直径的定义，Q一定也在直径上。而且因为离直径上的点最远，它还是直径的一个端点。

2.P不在直径上。

我们用反证法，假设此时PQ不是直径，AB是直径。

1

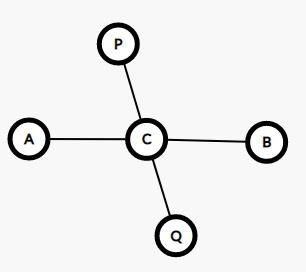
第一种情况，如图，若AB与PQ有交点C，由于P到Q最远，那么PC+CQ>PC+CA，所以CQ>CA，易得CQ+CB>CA+CB，即CQ+CB>AB，与AB是直径矛盾，所以假设不成立。（其中AB，PQ不一定是直线，画成直线是为了方便）

2

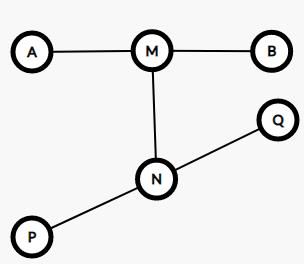
第二种情况，如图，若AB与PQ没有交点，M为AB上任意一点，N为PQ上任意一点。首先还是NP+NQ>NQ+MN+MB，同时减掉NQ，得NP>MN+MB，易知NP+MN>MB，所以NP+MN+MA>MB+MA，即NP+MN+MA>AB，与AB是直径矛盾，所以这种情况也不成立。

证毕。

---

代码

\(BFS版\)。

#include
using namespace std;
struct node
{
    int to,w,next;
} e[100010*2];
int head[100010],f[100010],n,m,tot;
bool vis[100010];
void add_edge(int from,int to,int cost){e[++tot].next=head[from],head[from]=tot,e[tot].to=to,e[tot].w=cost;}
void bfs(int v)
{
    queue  q;
    while(!q.empty()) q.pop();
    memset(f,0,sizeof(f));
    memset(vis,0,sizeof(vis));
    q.push(v);
    vis[v]=1;
    while(!q.empty())
    {
        int x=q.front();
        q.pop();
        for(int i=head[x];i;i=e[i].next)
            if(f[e[i].to]==0&&!vis[e[i].to])
            {
                f[e[i].to]=f[x]+e[i].w;
                q.push(e[i].to);
            }
    }
}
 
int main()
{
    int u,v,w;
    scanf("%d%d",&n,&m);
    tot=0;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        add_edge(u,v,w);
        add_edge(v,u,w);
    }
    bfs(1);
    int maxn=0;
    for(int i=1;i<=n;i++)
        if(f[i]>f[maxn])maxn=i;
    bfs(maxn);
    int ans=0;
    for(int i=1;i<=n;i++)
        if(f[i]>ans)ans=f[i];
    printf("%d\n",ans);
    return 0;
}

---

\(DFS\)版

#include

using namespace std;

long long dst[200010],t,dep[200010],son[200010],maxx,head[200010],ff[200010],vis[200010];
long long s,l,r,ans,n,m,num;

struct node
{
    int to,nex;
    long long v;
}e[400010];

void add(int from,int to,long long v)
{
    e[++num].to=to;
    e[num].v=v;
    e[num].nex=head[from];
    head[from]=num;
}

void dfs(int x,int fa)
{
    for(int i=head[x];i;i=e[i].nex)
    {
        int v=e[i].to;if(v==fa)continue;
        ff[v]=x;
        dst[v]=dst[x]+e[i].v;
        dfs(v,x);
    }
}


int main()
{
    cin>>n;
    for(int i=1;i>u>>v>>w;
        add(u,v,w);
        add(v,u,w);
    }
    
    dfs(1,0);
    
    for(int i=1;i<=n;i++)
        if(dst[i]>maxx)maxx=dst[i],s=i,dst[i]=0;
        
    dfs(s,0);
    
    maxx=0;
    
    for(int i=1;i<=n;i++)
        if(dst[i]>maxx)maxx=dst[i],t=i;
        
    printf("%lld\n",maxx);
    
    return 0;
}