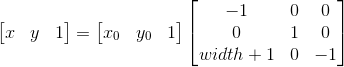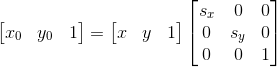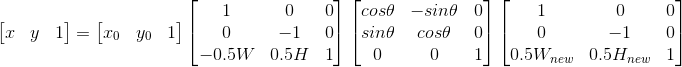几何变换为在不改变图像内容的前提下,对图像像素进行相对空间位置移动的处理方式。包括了平移、镜像、转置、缩放旋转等。
基本理论
变换方式
图像几何变换就是建立源图像与变换后图像之间的映射关系。
可以分为向前映射与向后映射
向前映射
数学公式如图,只要给出输入像素坐标,即可获得变换后的坐标。
不过向前映射存在如下问题
- 易产生浮点数坐标,如(1.5,1.5)便是无效坐标
- 映射不完全和映射重叠。如放大和缩小。
向后映射
由输出图像坐标反过来推算该像素在源图像的位置。实际处理中基本应用向后映射。
平移变换
平移变换就是将所有坐标分别加上指定的垂直偏移量。
镜像变换
镜像变换是以中线为轴,进行对称变换。
width为图像宽度。以矩阵形式表示,如下
matlab中可以使用maketform()与imtransform()函数来进行变换。
图像的转置
图像的转置就是将横坐标与纵坐标交换位置。转置后图像宽度与高度对调。
图像的缩放
图像的缩放数学表达式为:
其中,sx与sy为缩放系数。这里采用的是向后映射。
在影射过程中,会产生浮点坐标像素,它可以通过一系列算法获得浮点坐标的近似值。
常见插值法有最邻近插值法、双线性插值法与二次立方插值法
- 最邻近插值法:
即为四舍五入,像素值等于离该点最近的输入图像像素值。会产生马赛克锯齿。 - 双线性插值法:
将四个点的像素值按照一定比例混合,得到改浮点像素值。
距离哪个点更近,这个点得到的权重就越高。
双线性插值需要进行3次线性插值,才可以得出最终的结果。
MATLAB中使用imresize函数来进行缩放:
g = imresize(f, scale);
图像的旋转
图像旋转过程中,需要将图像的坐标进行转换。转换成以中心点为原点的数学坐标系。需要3步:
- 由输入图像的坐标系转化为数学坐标系。
- 通过数学旋转坐标系计算指定像素旋转后的坐标。
- 由旋转坐标系转换为输出图像的坐标系。
矩阵表示为:
其中W,H为原图像的宽度与高度,而Wnew和Hnew是旋转后图像的宽高。
旋转过程中同样有浮点坐标的问题,也需要使用最邻近插值和双线性插值。
matlab中使用imrotate()函数进行旋转:
B = imrotate(A, angle, method, bbox)
method为插值方法,bbox用来制定是否重新定义尺寸。
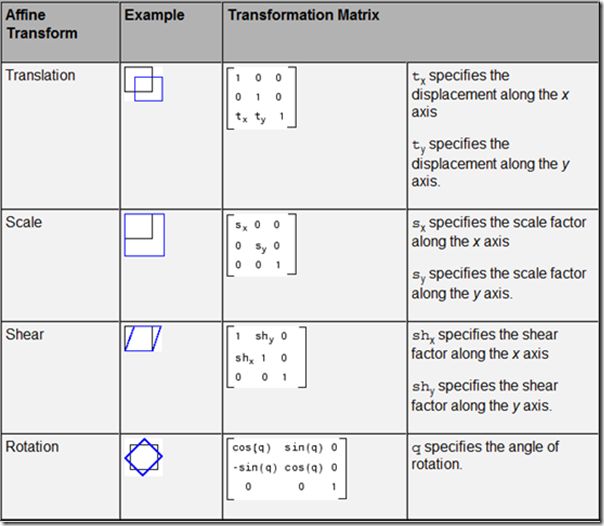
图像仿射变换
tform = maketform('affine', T);
g = imtransform(f, tform, interp);
其中,interp可以是'nearest','bilinear'或者'bicubic'。
以上内容来自《数字图像处理:原理与实践(matlab版)》左飞著,电子工业出版社。此为学习笔记。