一说给孩子做数学启蒙,
99%的中国家长第一反应就是 ——
1,2,3,4.....
然后就是
1+1,1+2,2+2......
很多父母就是这样急于求成, 注重结果忽略过程和基础,把数数和运算当成数学的主要部分。
认为这种数学启蒙越早越好,在孩子还没有数字的概念的情况之下就被要求从1数到100,被迫的去记一些加减运算的式子。
但这种教育模式,教的并不是数学,只是计算。甚至有时候连计算都不是,只是背诵。
所以,对于很多孩子或者成人而言,数学是一个重复、无聊的东西,许多人都曾经有过谈“数”色变时候。
那什么是真正的数学启蒙?
数学启蒙的重点,不在于早和教的多复杂,更多的是在生活中潜移默化的教导孩子数的概念。
孩子需要更全面、更“本质”的数学启蒙教育,来替代简单的数数。借助合适的方法、有效的工具和恰当的资源,孩子可以从数学启蒙中受益良多。
以“触摸”为主的数学启蒙
适用于0-3岁
这个阶段的孩子是通过触觉来认识世界的,应该从生活中的实物入手,比如说数字饼干、益智的数字积木等,要让孩子有一种手感,来认识数字这个概念。
这里要介绍一下蒙氏教育的创始人,蒙台梭利老太太讲过的一个案例。
有一次她去某个幼儿园参观,看到老师在教孩子形状 —— “三角形有三个顶点,有三条边”。她则认为这是非常错误的教学方法,在著作中特地批判了一下。她认为儿童很难理解这些被成人归纳出来的抽象数学概念以及定义,对于儿童来说,重要的不是掌握三角形的几条边,几个角,每个角是锐角直角还是钝角,而是切实地用身体去感知这个形状。
孩子对于物体的感知是更全面和具象的,因此一块形状标准的积木,让孩子一直把玩摸索堆砌,在过程中,孩子就可以逐渐确认对三角型以及其他形状的感观。等到了小学、中学阶段掌握抽象的几何知识时,则会事半功倍。
以“看见”为主的数学启蒙
适用于3-6岁
孩子逐渐长大,视觉感官逐渐作为主导,对于这个阶段的孩子来说,应该用更具体的概念加以强化。你要让他能够看到数字概念的呈现,来加深数字的概念
看见数字的概念
——看到“0”
随便找一个人,如果你问他:零是什么?他八成会告诉你:零就是没有。
《汉声数学》中有一本书的书名就叫做《零不只是没有》。那零还可以是什么?
零可以是比赛的起点,重量的起点,测量的起点。
零还可以当做分割点。在温度计上,0是水结冰和融化的分割点。零不只是没有,它还有很多种功能。
——看到“10”
从1数到9,孩子通常都会觉得很简单。但到了进位后的数字10,不少孩子就会转不过弯来。
数字“10”中的“1”代表了什么?要想让孩子明白,十位数上的“1”代表了10,可没那么容易。
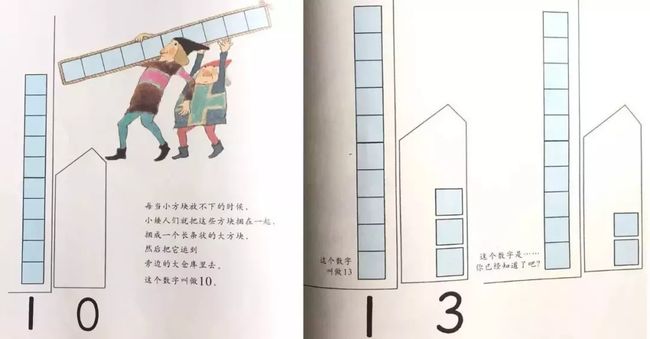
安野光雅的《走进奇妙的数字世界》在讲解10以上的数字时,用了非常奇妙的方式。
每个数字都有自己的名字。0到9的概念,通过这些整齐排放的小方块,一目了然。哎呀,最后一个,放不下了!
每当小方块放不下时,小矮人就把这些方块捆成一个长条状的大方块,把它运到旁边的大仓库去。这个数字叫做10。以此类推。
通过具象的解说,孩子理解了数字10的概念,也知道了这里的数字“1”和“0”代表的是什么。
看见尺寸、时间、重量…
成人观念中的尺寸、重量、时间其实都是被抽象化的,对于孩子来说,这种抽象概念的意义不大,启蒙教育阶段,依旧是应该用更具体的概念加以强化。
举个家长最熟悉的例子,妈妈要出门了,宝宝问几点回来,如果你跟ta说,下午5点,那就完蛋了。因为孩子根本不懂得下午5点是什么。像2个小时,30分钟这种说法,对孩子也是无效的。
“一集动画片的长度”、“你睡醒午觉下楼玩一圈之后”、“天变黑了”,这些就是宝宝更容易体会和掌握的了。
在学会计数之后,可以将这些概念更抽象化一些,但可能暂时还用不上我们的“单位制” —— 这里到墙边有多远?对于孩子来说,这种问题的答案就不应该是几米,而是几步,或者几块地砖。
以空间为主的数学启蒙
适用于3-6岁 、 6岁+
我们生活在一个三维空间,因此数学中的空间关系概念,是未来从立体几何、制图、3D设计到建筑工程等无数领域都需要运用到的基础能力。同样的,我们在启蒙阶段,完全不需要用抽象的概念来去引导孩子,而是让他们从实际生活中体验“空间是三维的”。
针对3-6岁的孩子,我们可以从简单又常见的积木入手。
比如一块积木的长宽高,其实就代表着三维空间中的3个维度,那么通过不同的拼搭方式,我们就可以得到不同的形状。
而将拼摆过的结果和最初的形状进行对比,帮助孩子初步理解三种空间相互关系的对比:长-短,粗-细,厚-薄。
针对6岁+的孩子,则可以进一步利用一些教学类的玩具帮助孩子学习掌握抽象的数学知识,提升多种智能。
观察积木块特征,探索积木块之间的关系,学习立方体的体积概念。
以思维为主的数学启蒙
适用于6岁+
这个阶段的孩子具有一定的逻辑思维能力,需要进一步引导孩子独立思考,发现规律、总结规律,利用规律,激发孩子的想象力和创造力。
在游戏中锻炼孩子们逻辑推理能力、统筹规划能力、条理性思维——
一次只能移动一个圆盘,小圆盘上面不能放大圆盘,如何将这8块圆盘以最少的步数移到另一根上面?
如何走好下一步?如何能获胜?
需要有策略的规划好每一步,具有全局思维。
单人游戏,如何走棋,用最少的步数让最后一颗棋子落在最中间?需要空间规划能力、条理性思维和专注精神。
将1-12填入棋盘指定的交叉点上,使纵向、横向及对角线上的四数之和等于26。
这种能力,不仅仅是在未来的数学考试中任何一道题目的解题能力,也代表着我们未来进入社会,如何去面对和处理更复杂的工作项目乃至人际关系的能力。
。
。
具象而非抽象,感知而非背记。
用好玩具、游戏以及家中日常用品,通过娱乐和生活,感知数学的基本感念,这是数学启蒙的核心要求。
建立好这些概念,培养好孩子从具象到抽象,从事物到规律的能力,当他们在未来学习更抽象和理论化的数学知识时,就可以掌握的更顺畅。
数学,是一个远远超过四则计算的庞大体系 —— 概率、分析、集合、代数、几何、拓扑......
数学,它蕴含在我们生活中的各个方面,是这个世界的基础法则。
未来,数学这门学科的大楼能够建得多高、多牢固,数学启蒙都起到奠定基石的作用。