线段树是个很强大的数据结构,它的阉割版是树状数组.
因为它能够很快速的处理单点和区间的查询及修改,所以这个~~ 毒瘤 优秀数据结构很受OIer的 唾弃 ~~喜爱。
线段树的本质是一棵二叉搜索树~~ 果然很毒瘤 ~~
它的每一个结点,都存储了一个区间内的信息,当然,叶子结点只存储了一个点的信息。
因为这个特性,所以每个结点都必须要包含:
左端点,右端点以及两个端点之间所包含的值。
基本思想是** 二分 **。
根节点包含了所有值的和,从根节点向下,每个结点都代表一段区间的值,直到叶子结点。
当然,它的基本思想是二分,所以包含区间[l,r]的结点的左儿子包含[l,mid],右孩子包含[mid+1,r]。
所以对于结点k,它的左儿子编号为2×k,右儿子编号为2×k+1.
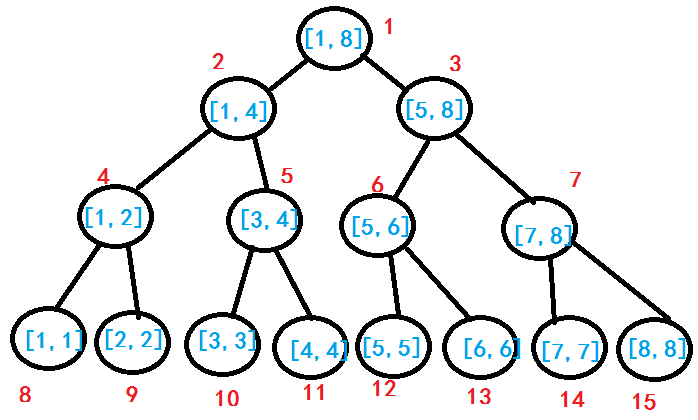
比如这就是一棵存储了八个数据的线段树。从中我们不难发现,每个父亲结点都是它两个儿子结点的区间值的和。可以用递归利用这个特性建树。
怎么返回呢?当然是到了叶子结点返回。在上图中很明显,叶子结点的特征就是:存储区间的左右端点相同。
利用这个性质完成后面的基本操作。
主要讲讲线段树的基本操作。
0.存储。
存线段树要开四倍结构体空间,因为它很毒瘤
struct node
{
long long l,r,w;
}tree[4*100000+10];1.建树。我们在建树的过程中就要维护好线段树的性质。
所以我们不妨从根节点往下递归,每次都分别访问当前节点的两个儿子,直到它是叶子结点才输入值,访问之后就可以更新当前节点的区间值了。
inline void build(long long l,long long r,long long k)//建树
{
tree[k].l=l,tree[k].r=r;
if(l==r)
{
scanf("%d",&tree[k].w);
return;
}
long long m=l+(r-l)/2;
build(l,m,k*2);
build(m+1,r,k*2+1);
tree[k].w=tree[k*2].w+tree[k*2+1].w;
return;
}大概思路应该很容易就能理解:递归到自己的所有儿子(叶子结点没有儿子)都有准确值的时候,更新自身的值。
2.单点查询。
因为线段树的每一个结点都是包含的一段数据的和,所以如果要求单点,需要递归到最后一层,即叶子结点才能返回。
依然采用二分,选择自己的左右孩子递归,直到找到我们想要的点的值返回。
inline long long ask(long long k)
{
if(tree[k].l==tree[k].r)
return tree[k].w;
long long m=tree[k].l+(tree[k].r-tree[k].l)/2;
if(x<=m)return ask(k*2+1);
else return ask(k*2);
}3.单点修改。
单点修改在线段树里面需要修改的值不止一个。
因为我们更新的点如果不是根节点,那么它会有祖先结点。它的所有祖先节点都包含了它的值,在它修改之后,这些点的值也需要更新。所以我们在完成修改操作递归返回的时候,我们再更新一下一路上经过的点的值(左右孩子结点值相加)。
inline void add(long long k)
{
if(tree[k].l==tree[k].r)
{
tree[k].w+=y;
return;
}
if(tree[k].f)down(k);
long long m=tree[k].l+(tree[k].r-tree[k].l)/2;
if(x<=m)add(k*2+1);
else add(k*2);
tree[k].w=tree[k*2].w+tree[k*2+1].w;
return;
}4.区间查询。
区间操作是线段树中较难的~~ (废话) ~~
假设我们要查询区间[x,y]的和值,当前递归这一个结点包含的区间是[l,r]。
分情况看吧。
1.[l,r]完全被[x,y]包含。因为是包含的,所以直接加到答案上。
2.[l,r]被[x,y]包含一部分。不急着加,继续二分到情况1为止。
3.[x,y]完全被[l,r]包含。根据二分继续递归即可。
每次对l,r算mid,用x,y分别比较mid,当y<=mid,说明[x,y]全在当前区间的左子区间,往左走,x>mid说明全在右子区间,往右走。
如果没有这种特殊情况,那就两个一起走。
说下2的思路。
很明显,按照2的思路走下去,最坏情况会递归到叶子结点,这时一定满足1的条件。
inline void getsum(long long k)//区间查询[a,b]
{
if(tree[k].l>=a&&tree[k].r<=b)
{
ans+=tree[k].w;
return;
}
long long m=tree[k].l+(tree[k].r-tree[k].l)/2;
if(a<=m)getsum(k*2);
if(b>m)getsum(k*2+1);
}5.区间修改
最难的一个玩意。
区间修改因为涉及到的结点太多,查询的话时间浪费很严重。
怎么办呢?
只查询对修改有帮助的
需要引入一个新东西,叫做懒标记。
懒标记的作业何在呢?它能够实现只查询需要的点。
为什么叫懒标记?** 只有需要用到它的时候它才会动。
前面的单点修改,在更新后是一路修改回来。
而懒标记可以把这些要修改的信息暂时存储起来,需要求值的时候在恢复回去。
怎么实现。
首先得存储对吧,结构体里面加个变量f来存储懒标记。
递归到哪个节点,就仅更新哪个节点的状态,并把当前更改值累积**到懒标记中。
为什么一定是累积?因为我们可能会多次更新点的懒标记值但是不使用,这个时候就要把它记录下来,需要使用的时候再进行修改即可。
而什么时候需要使用到这个懒标记呢?
当我们要更新一个点它所有的子节点的值的时候,我们就依次把懒标记下传(更新值)就可以了。当然,两个儿子结点都要传。
那么讲讲下传操作吧。
根据上面的定义,无非就是:
更新两个孩子结点的区间值。
当前结点懒标记清零。
特殊的,我们也要把父亲节点的懒标记值在清零之前累加给自己的孩子结点的懒标记值(传到叶子结点为止)
这样三步操作,就完成了懒标记的下传。
inline void down(long long k)//把懒标记下传
{
tree[k*2].f+=tree[k].f;
tree[k*2+1].f+=tree[k].f;
tree[k*2].w+=tree[k].f*(tree[k*2].r-tree[k*2].l+1);
tree[k*2+1].w+=tree[k].f*(tree[k*2+1].r-tree[k*2+1].l+1);
tree[k].f=0;
return;
}因为有了懒标记这个东西,所以前面的2-4以及现在的5都需要加上懒标记下传这一步。
即:如果当前递归到的结点的懒标记值不为0,那么下传它
if(tree[k].f)down(k);在上述四个操作的递归临界判断完之后添加就可以了。
基本上就是这样,下面贴代码:、
#include
using namespace std;
long long p,n,m,x,y,a,b;
long long ans;
struct node
{
long long l,r,w;
long long f;//懒标记
}tree[4*100000+10];
inline void down(long long k)//把懒标记下传
{
tree[k*2].f+=tree[k].f;
tree[k*2+1].f+=tree[k].f;
tree[k*2].w+=tree[k].f*(tree[k*2].r-tree[k*2].l+1);
tree[k*2+1].w+=tree[k].f*(tree[k*2+1].r-tree[k*2+1].l+1);
tree[k].f=0;
return;
}
inline void build(long long l,long long r,long long k)//建树
{
tree[k].l=l,tree[k].r=r;
if(l==r)
{
scanf("%d",&tree[k].w);
return;
}
long long m=l+(r-l)/2;
build(l,m,k*2);
build(m+1,r,k*2+1);
tree[k].w=tree[k*2].w+tree[k*2+1].w;
return;
}
inline void k_add(long long k)//区间修改
{
if(tree[k].l>=a&&tree[k].r<=b)
{
tree[k].w+=(tree[k].r-tree[k].l+1)*y,
tree[k].f+=y;
return;
}
if(tree[k].f)down(k);
long long m=tree[k].l+(tree[k].r-tree[k].l)/2;
if(a<=m)k_add(k*2);
if(b>m)k_add(k*2+1);
tree[k].w=tree[k*2].w+tree[k*2+1].w;
return;
}
inline long long ask(long long k)//单点查询
{
if(tree[k].l==tree[k].r)
return tree[k].w;
if(tree[k].f)down(k);
long long m=tree[k].l+(tree[k].r-tree[k].l)/2;
if(x<=m)return ask(k*2+1);
else return ask(k*2);
}
inline void add(long long k)//单点修改
{
if(tree[k].l==tree[k].r)
{
tree[k].w+=y;
return;
}
if(tree[k].f)down(k);
long long m=tree[k].l+(tree[k].r-tree[k].l)/2;
if(x<=m)add(k*2+1);
else add(k*2);
tree[k].w=tree[k*2].w+tree[k*2+1].w;
return;
}
inline void getsum(long long k)//区间查询[a,b]
{
if(tree[k].l>=a&&tree[k].r<=b)
{
ans+=tree[k].w;
return;
}
if(tree[k].f)down(k);
long long m=tree[k].l+(tree[k].r-tree[k].l)/2;
if(a<=m)getsum(k*2);
if(b>m)getsum(k*2+1);
}
int main()
{
scanf("%lld%lld",&n,&m);
build(1,n,1);
for(long long i=1;i<=m;i++)
{
scanf("%lld",&p);
ans=0;
if(p==1)
{
scanf("%lld%lld%lld",&a,&b,&y);
k_add(1);
}
else
{
scanf("%lld%lld",&a,&b);
getsum(1);
cout< main函数是因为要过luogu的板子题,请自行修改。
ov.