N皇后问题
以八皇后为例,在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,皇后可以在其所在位置的对应的行,列,对角线,反脚线上发动攻击,请问一共有多少种摆法.
如果我们将这里的8拓展一下,变成N,那么这个问题就变成了N皇后问题.
算法
下面是算法的高级伪码描述,这里用一个
N*N的矩阵来存储棋盘:
- 算法开始, 清空棋盘,当前行设为第一行,当前列设为第一列;
- 在当前行,当前列的位置上判断是否满足条件(即保证经过这一点的行,对角线与反对角线上都没有两个皇后),若不满足,跳到第
4步;- 在当前位置上满足条件的情形:
在当前位置放一个皇后,若当前行是最后一行,记录一个解;
若当前行不是最后一行,当前行设为下一行, 当前列设为当前行的第一个待测位置;
若当前行是最后一行,当前列不是最后一列,当前列设为下一列;
若当前行是最后一行,当前列是最后一列,回溯,即清空当前行及以下各行的棋盘,然后,当前行设为上一行,当前列设为当前行的下一个待测位置;
以上返回到第2步;- 在当前位置上不满足条件的情形:
若当前列不是最后一列,当前列设为下一列,返回到第2步;
若当前列是最后一列了,回溯,即,若当前行已经是第一行了,算法退出,否则,清空当前行及以下各行的棋盘,然后,当前行设为上一行,当前列设为当前行的下一个待测位置,返回到第2步;
算法不算复杂,可是各种实现的速度却千差万别,不过解决N皇后问题主体思想就是回溯法,说白了,就是依靠一次一次地搜索(暴力法)来得到最终的结果.这篇文章的话,我想讲一个用位移运算实现的N皇后求解程序,相对而言,这是一个非常高效的实现.
代码实现
#include
#include
#include
#include
using namespace std;
struct BackTracking
{
const static int kMaxQueens = 20; // 最多支持20皇后
const int N;
int64_t count;
// bitmasks, 1 means occupied, all 0s initially
uint32_t columns[kMaxQueens]; // cloumns[row]的值对应的bit位表示在第row行中,有哪些位置已经被占用了
uint32_t diagnoal[kMaxQueens]; // 对角线方向,哪些位置已经被占用了
uint32_t antidiagnoal[kMaxQueens]; // 反对角线,哪些位置已经被占用了.
BackTracking(int nqueens)
: N(nqueens)
, count(0)
{
assert(0 < N && N <= kMaxQueens);
memset(columns, 0, sizeof columns);
memset(diagnoal, 0, sizeof diagnoal);
memset(antidiagnoal, 0, sizeof antidiagnoal);
}
int ctz(int n) // 对n对应的bit位从右边开始数,第一个1之后0的个数
{
assert(n != 0);
int count = 0;
while (!(n & 1)) {
n = n >> 1;
count++;
}
return count;
}
void search(const int row)
{
uint32_t avail = columns[row] | diagnoal[row] | antidiagnoal[row]; // 找出有哪些位置可以放皇后
avail = ~avail; // 得到这一行,哪些位置是可以用的
while (avail) {
// ctz(avail)用于找出avail对应的bit位右起第一个1后面有多少个0
// 举个例子,如果avail=6,对应的二进制数为1100,那么ctz(6)=2
// avail=4,即0x1000,ctz(4)=3
// 换句话说,就是找到第1个可以放置的位置的下标
int i = ctz(avail);
if (i >= N) {
break;
}
if (row == N - 1) { // 已经是最后一行,得到一个解
++count;
}
else {
const uint32_t mask = 1 << i; // 将要放置的位置对应的mask
columns[row + 1] = columns[row] | mask; // 下一行的mask位置,这个位置已经被占用了,对应绿色的线
diagnoal[row + 1] = (diagnoal[row] | mask) >> 1; // 对角线方向是朝右下方移动的,对应蓝色的线
antidiagnoal[row + 1] = (antidiagnoal[row] | mask) << 1; // 反对角线方向是朝左下方移动的,对应红色的线
search(row + 1); // 继续往下搜索
}
// 运行到了这里的话,说明前面选择的位置i不可行,所以要将第i位上的bit关闭
// 我们来举一个例子,假设avail是6,即1100,则6-1=5,即1011
// 1 1 0 0
// & 1 0 1 1
//------------
// 1 0 0 0
// 可以看得到的是,恰好屏蔽了最后一个bit位,就这样不断选择可以放入的位置
avail &= avail - 1; // turn off last bit
}
}
};
int64_t backtrackingsub(int N, int first_row, int second_row) // N指的是皇后的个数
{
// first_row表示queen放在第一行放在哪一个位置上
// second_row表示queen放在第二行的哪一个位置上
const uint32_t m0 = 1 << first_row; // 得到位置的mask
BackTracking bt(N);
bt.columns[1] = m0; // 第1行的first_row这个格子已经不能放入
bt.diagnoal[1] = m0 >> 1; // 对角线
bt.antidiagnoal[1] = m0 << 1; // 反对角线上有一些位置也已经不能使用了
if (second_row >= 0) // 如果第2个位置上也放置了值的话
{
const int row = 1;
const uint32_t m1 = 1 << second_row;
uint32_t avail = bt.columns[row] | bt.diagnoal[row] | bt.antidiagnoal[row];
avail = ~avail; // avail所指带的bit为1表示该位置可以放queen,否则不行
if (avail & m1)
{
bt.columns[row + 1] = bt.columns[row] | m1; // 第2行
bt.diagnoal[row + 1] = (bt.diagnoal[row] | m1) >> 1;
bt.antidiagnoal[row + 1] = (bt.antidiagnoal[row] | m1) << 1;
bt.search(row + 1);
return bt.count;
}
}
else
{
bt.search(1); // 否则的话,表示不限制第2行皇后的位置
return bt.count;
}
return 0;
}
int main(int argc, char* argv[])
{
int N = 13;
int64_t count = 0;
for (int i = 0; i < N; ++i) {
count += backtrackingsub(N, i, -1); // 八皇后问题的解的个数
}
printf("%d\n", count);
system("pause");
}
一个例子
关于上面的核心代码search,我这里举一个栗子.当然,行为不完全一致,但是读了这个例子之后,你理解上面的代码会简单很多.
在开始之前,我们有这样一个结构:
uint32_t columns[N]; // cloumns[row]的值对应的bit位表示在第row行中,有哪些位置已经被占用了
uint32_t diagnoal[N]; // 对角线方向,哪些位置已经被占用了
uint32_t antidiagnoal[N]; // 反对角线,哪些位置已经被占用了.
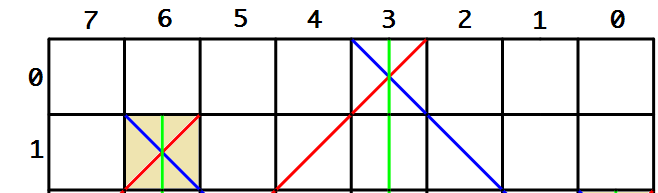
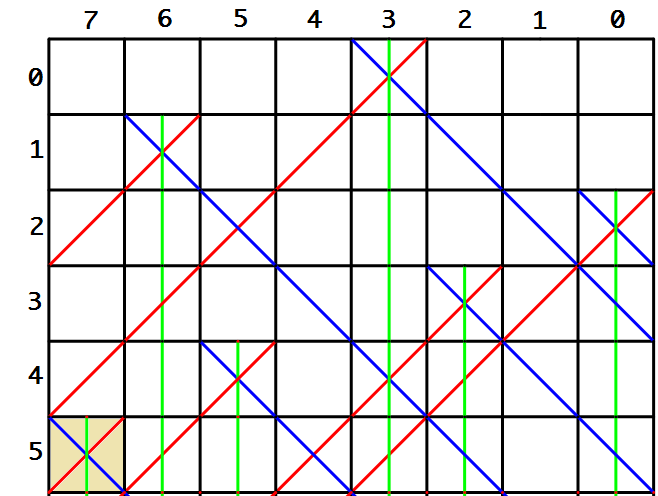
假设我们将第1个皇后放在第0行的下标为3的格子中,下图标记了这个位置,请不要吐槽列的标记为什么不反过来,因为标记正着反着没有多么大的关系,但是反着标记的话,它和我们的直觉是相符的.可以帮助我们更好地理解.
那么对于第1行来说,有这么一些位置是不能够使用了的:
所以:
columns[1] = 0x0001000; // ==> 第1行第3格
diagnoal[1] = 0x0001000 >> 1; // ==> 第1行第2格
antidiagnoal[1] = 0x0001000 << 1; // ==> 第1行第4格
对应到下面的图中,就是第1行的2, 3, 4格不能填写了,我们可以这样来取得能够放入的位置:
avail = columns[1] | diagnoal[1] | antidiagnoal[1]; // 0x00011100
// 然后取反,然后avail对应的bit位为1所对应的位置就可以放入皇后啦.
avail = ~avail; // 0x11100011
这样的话,在第1行填入我们随意选择一个位置吧,就把皇后放到第6格好了,该位置对应的mask = 0x01000000.
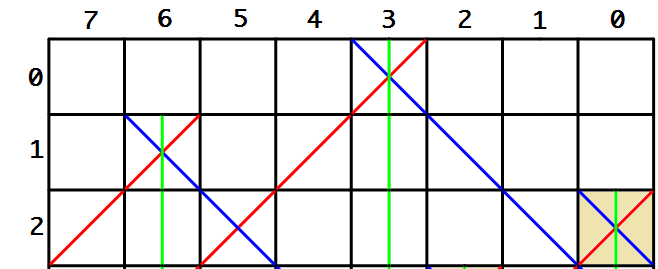
填入之后,我们继续来限制第2行能够填入的格子.
显然对于上图中绿色的线条,添加上第2行的皇后所在的位置后,后要继续往下延伸:
columns[2] = columns[1] | mask; // 0x0001000 | 0x01000000 = 0x0101000; ==> 第6,3个格子不能填入
蓝色的对角线元素填上皇后的新位置后,要向右下方延伸:
diagnoal[2] = (diagnoal[1] | mask) >> 1; // 0x01000100 >> 1 = 0x00100010; ==> 第5,1个格子不填
绿色的反对角线元素填上皇后新位置后继续向左下方延伸:
antidiagnoal[2] = (antidiagnoal[1] | mask) << 1; // ==> 第7,5个格子不能填入
即:
现在我们在第2行选择了第0个格子,所以mask=0x00000001.
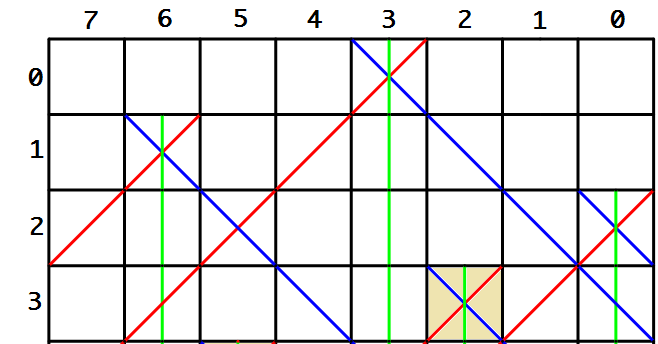
所以在第3行,我们有了这么一些限制:
columns[3] = columns[2] | mask; // ==> 第6,3, 0个格子不能填入
diagnoal[3] = (diagnoal[2] | mask) >> 1; // ==> 第4,0个格子不填
antidiagnoal[3] = (antidiagnoal[2] | mask) << 1; // ==> 第7, 1格子不能填入
我们这一次选择第3行的第2个格子放入皇后,那么接下来将会演变成下图这样:
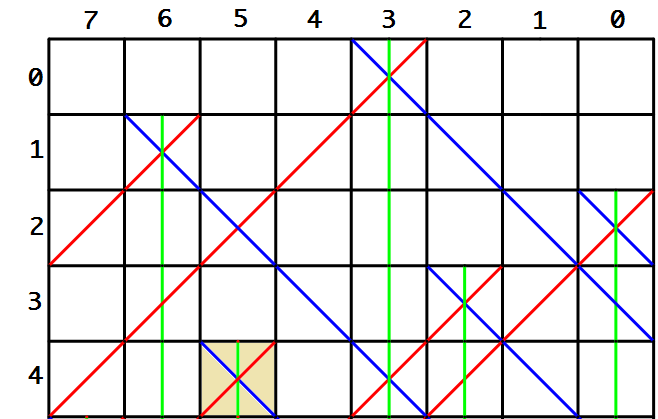
在第4行的第5个格子放入皇后,我们可以接着做下去:
我们继续在第5行的第7个格子中放入皇后,接下来如图:
在第6行已经没有格子允许我们放入了,这显然是一个错误的摆法,所以要退回去,这就是所谓的回溯,接下来的步骤我就不一一演示了.
参考
N皇后问题的两个最高效的算法