实现一个神经网络模型

“不闻不若闻之，闻之不若见之，见之不若知之，知之不若行之；学至于行之而止矣” ，一直在看理论，感觉差不多可以动手实现一个自己的神经网络了，正好最近没什么事情，干起来老铁。

这篇文章使用python（但是并没有使用 pytorch tensorflow 等深度学习框架）实现一个可以对 mnist 数据集手写数字图片进行识别的神经网络。因为使用的是 SGD 方法所以还是比较经典的一个神经网络，我们之后会对它进行升级改造（目前感觉可以改成 PB 的这样运算速度更快）。阅读这篇文章需要先对一些基本概念有一定的了解。

在实现我们的神经网络模型主体之前呢，我们先一个一个实现一些常用的函数。注意我们之后在学习的时候是使用 mini-batch 学习的所以在实现函数的时候需要注意这一点（遇到的一个大坑，一直在报错，后来终于找到了orz）

1. 激活函数

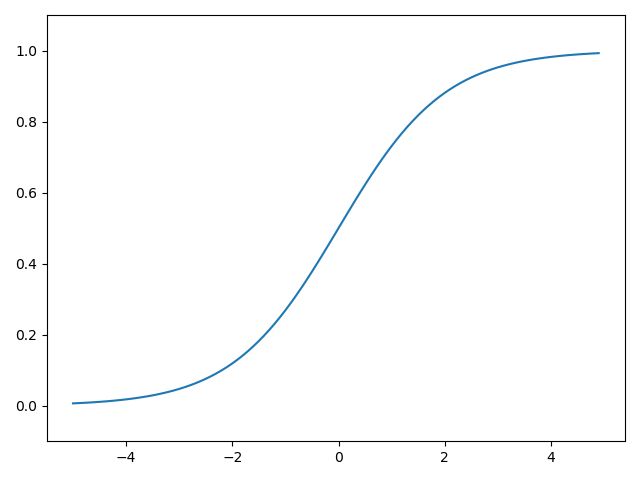
一个比较常用的激活函数是 sigmoid 函数：

这个实现很简单，注意这里面的 x 是向量而不是一个数。所以我们采用 numpy 来实现。

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

写完之后我们顺便测试一下。

import matplotlib.pyplot as plt
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

好的没问题，熟悉的平滑曲线~

因为我们的目标是为手写数字分类，作为一个分类问题，为了使输出有一定的意义（这个图片对应这个标签概率），第二层的输出我们考虑使用 softmax() 函数。

Softmax函数实际上是有限项离散概率分布的梯度对数归一化。因此，Softmax函数在包括多项逻辑回归，多项线性判别分析，朴素贝叶斯分类器和人工神经网络等的多种基于概率的多分类问题方法中都有着广泛应用。(这句极其官方的话来自百度百科)

在实现这个函数的时候有一个问题需要注意，注意到这个函数里面存在指数运算，所以在编程的时候就要考虑内存溢出问题，注意到：

这意味着我们对输入信号加上或者减去一个常数并不会影响到结果，一般来说我们都是减去信号中的最大值。

def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y

我们还是测试一下

>>> a = np.array([0.3, 2.9, 4.0])
>>> y = softmax(a)
>>> print(y)
[0.01821127 0.24519181 0.73659691]
>>> np.sum(y)
1.0

2. 损失函数

神经网络需要根据某个指标（或者说是线索）寻找最优权重，损失函数的值就是这个线索。我们最终的目标就是想找到一组参数，使得损失函数达到最小值（一般来说是接近最小值）。
常见的损失函数有，均方误差和交叉熵误差，我们采用交叉熵误差来实现我们的模型。

每次看到这个交叉熵误差，总是让我想起信息熵，不知道有没有什么联系。

回到正题，交叉熵看上去很复杂，但是对于来说，只有正确解的标签是 1 其他都是 0 。所以这个公式实际上就是计算了对应正确解标签的输出的自然对数。因为有对数运算的存在，所以我们需要添加一个微小值，避免负无限大的出现。我们可以先简单的这样实现：

def cross_entropy_error(y, t):
      delta = 1e-7
      return  -np.sum(t * np.log(y + delta))

同样的为了适应我们的 mini-batch 我们还需要进行一些修改：
我们可以将交叉熵误差修成下面这种形式;

看上去很复杂其实就是将原来单独的一个列向量，增加了列数，变成了一个矩阵，对每一列求一下交叉熵，然后求和取平均值。

def cross_entropy_error(y, t):
    # mini-batch one-hot 版本
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
    if t.size == y.size:
        t = t.argmax(axis=1)

    batch_size = y.shape[0] # y.shape (100, 10)  100个10维数组
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

3. 求梯度

类似于 这种由函数的偏导数组成的向量称为梯度。梯度指示的方向是各店处函数值减少的最多的方向。这里所说的梯度是指损失函数关于权重参数的梯度。我们为了实现简单，采用数值微分方法。
数值微分法求梯度简单点来说就是，保持其他变量不变（看成常数），对某一个变量求数值微分

实现如下：

def numerical_gradient(f, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)

    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)  # f(x+h)

        x[idx] = tmp_val - h
        fxh2 = f(x)  # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2 * h)

        x[idx] = tmp_val  # 还原值
        it.iternext()

    return grad

我们进行一个简单的测试，我们求一下下面这个函数在 处的梯度。

>>> def function_2(x):
...   return np.sum(x ** 2)
... 
>>> numerical_gradient(function_2, np.array([3.0, 4.0]))
array([6., 8.])

4. 二层神经网络模型

终于写完准备工作，到了我们激动人心的神经网络模型部分啦。因为神经网络模型包括了参数，还有各种方法，所以还是很适合使用面向对象的方法来实现的。

再次明确一下我们的目标：我们想设计一个神经网络实现对 mnist 的手写数字进行识别。
因为 输入的图片数据都是 28px X 28px 的灰度图像，所以我们可以将每张图片转化为一个长度为 784 的向量，那么输入层就确定为 784。
因为我们需要得到的结果是 0~9 的分类（实际上得到的是十个类别的概率，我们选择最高的一种作为分类的结果）所以确定输出层为 10。
那么只需要确定中间层就可以啦，这个需要最后根据结果做实验调整，我们暂时确定为 50。
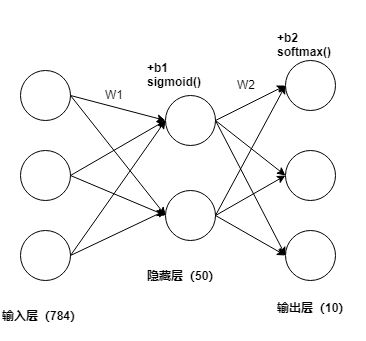
你可能有一个疑问，不是说好的两层的吗怎么有三层了呢，实际上我们一般把输入层叫做第 0 层，这样刚好有两层...
下面是设计图，作为实现的第一个神经网络，就没整什么池化层，卷积层，全部都是全链接层。（全连接对应着线性变换，也就是矩阵乘法）

先上源码：参考了斯坦福大学 CS231n 的源代码。

# coding: utf-8
# @Time   : 2019/7/11 15:27
# @Author : Vector_Wan
# @Email  : [email protected]
# File    : two_layer_net.py
# Software: PyCharm

import numpy as np
from common_funcs import sigmoid, softmax, cross_entropy_error, numerical_gradient, sigmoid_grad

class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        self.params = {'W1': weight_init_std * np.random.randn(input_size, hidden_size),
                       'b1': np.zeros(hidden_size),
                       'W2': weight_init_std * np.random.randn(hidden_size, output_size),
                       'b2': np.zeros(output_size)}

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
        # 第一层网络(Linear)
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        # 第二层网络(Linear)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        return y

    def loss(self, x, t):
        '''
        损失函数
        :param x: 输入数据
        :param t: 监督数据
        :return: 损失函数值
        '''
        y = self.predict(x)

        return cross_entropy_error(y, t)

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t)/float(x.shap[0])
        return accuracy

    def numerical_gradient(self, x, t):
        loss_W = lambda W:self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params["W1"])
        grads['b1'] = numerical_gradient(loss_W, self.params["b1"])
        grads['W2'] = numerical_gradient(loss_W, self.params["W2"])
        grads['b2'] = numerical_gradient(loss_W, self.params["b2"])

        return grads

下面我们一个一个方法来看：

首先是一个类的构造函数，这个函数需要给出模型的输入层神经元个数，隐藏层神经元个数，输出层神经元个数来确定模型的结构。（其实确定了参数矩阵的形状）
然后是对参数的初始化，这个初始化有点讲究，W 不能使用 0 来初始化，这样会导致神经网络没有学到任何东西! 这是因为所有神经元之间的对称性导致所有神经元在每次迭代中都具有相同的更新。因此，无论我们运行优化算法有多少次迭代，所有神经元仍会得到相同的更新，并且不会发生学习。因此，当初始化参数时，我们必须破坏对称性，以便模型将开始学习梯度下降的每次更新。

我们采用标准正态分布来初始化我们的参数。

接下来是一个预测函数，这个与之后的pb 神经网络的向前传播有一定的相似性。在我们的模型中这个函数主要是为了计算准确度和损失。预测函数实际上就是把数据传进去走一遍，因为都是全链接层，就都是一些矩阵的乘法。

实现了预测函数那么我们就可以计算损失和精度，首先先把数据放进去走一下，然后加上标签输入到计算损失和精度的函数中就可以。

最后是数值微分，因为我们需要对损失函数计算每一个关于参数的偏微分，但是这个参数是存在不同的矩阵里面的，所以得到的梯度肯定也是跟这些矩阵形状相同的几个矩阵。我们为了好辨识他们，将他们存在一个字典里面，key 就使用他们参数矩阵的名字。另外在计算梯度是时候，需要将损失函数传入，为了代码简单语义更加明确我们写了一个匿名函数传入。
好啦整个模型就弄好啦，我们最后让这个模型跑起来测试一下。

5. Run Model！

当时写到这里的时候想着终于可以 Run 啦然后，，，就迎来了一大堆错误，而且报的错还不是很有针对性，还是要靠你自己调试，，，然后就对着代码发呆了好几天，，，最后终于改好了，，，不解释了，，，

# @Time   : 2019/7/17 22:20
# @Author : Vector_Wan
# @Email  : [email protected]
# File    : test.py
# Software: PyCharm
import numpy as np
import matplotlib.pyplot as plt
from mnist import load_mnist
from two_layer_net import TwoLayerNet


# 导入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

# 全局变量
train_loss_list = []
train_acc_list = []
test_acc_list = []

# 超参数
iter_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
iter_per_epoch = max(train_size / batch_size, 1)

# 生成模型
net_work = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

# 模型的训练
for i in range(iter_num):
    # 获取 mini_batch
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    # 计算梯度
    grad = net_work.gradient(x_batch, t_batch)

    # 更新参数
    for key in ('W1', 'b1', 'W2', 'b2'):
        net_work.params[key] -= learning_rate * grad[key]

    # 记录学习过程
    if i % iter_per_epoch == 0:
        loss = net_work.loss(x_train, t_train)
        train_loss_list.append(loss)
        train_acc = net_work.accuracy(x_train, t_train)
        train_acc_list.append(train_acc)
        test_acc = net_work.accuracy(x_test, t_test)
        test_acc_list.append(test_acc)
        print('运行中... 损失：{} 训练集准确度：{}  测试集准确度：{}'.format(/
                                                                    loss, train_acc, test_acc))

经过 17 小时的训练，，，最后的结果是：

运行中... 损失：0.1871478162531592 训练集准确度：0.947  测试集准确度：0.9437

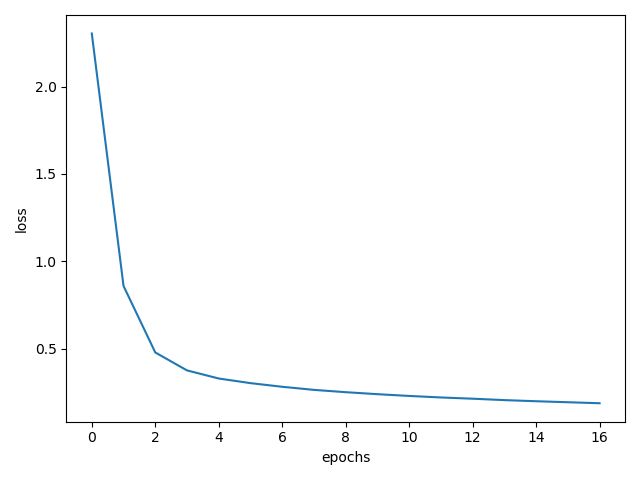
emmm还不错，就是时间太长了，因为我们是在 console 中运行的所以我们运行的数据都被保留了下来，我们将保存的数据可视化一下看看：
首先是损失函数，可以看到损失函数值在下降，这是一个好事情，说明我们的模型确实在学习，它的犯错率在下降。

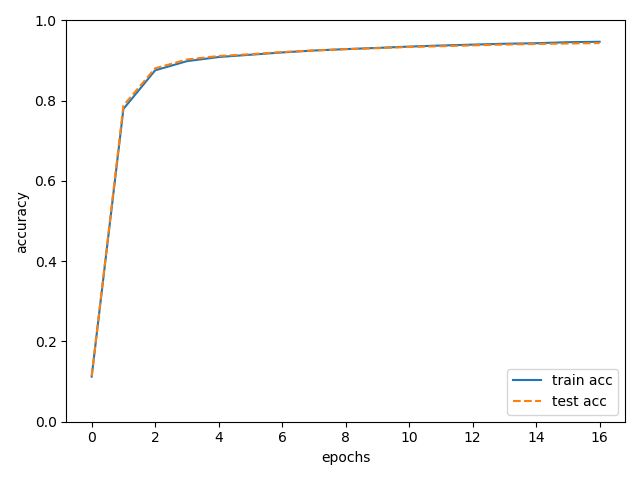
接下来我们来看看学习的精确度，基本上实在上升的，而且值得注意的是，我们的测试集准确度与训练集准确度直观上来看相差不大，这说明我们的模型并没有过拟合，具有一定的泛化能力。

接下来我们可以考虑对我们的性能进行一个提升，另外有一些参数还需要优化。这篇文章就写道这里吧。