编译:李琼琼 (山东大学)
Email: [email protected]
Source: Cattaneo, Matias, D, et al. Inference in regression discontinuity designs under local randomization[J]. The stata journal, 2016.
Stata连享会 计量专题 || 精品课程 || 推文 || 公众号合集
2020寒假Stata现场班
北京, 1月8-17日,连玉君-江艇主讲
2020连享会-文本分析与爬虫-现场班
西安, 3月26-29日,司继春-游万海 主讲 (附助教招聘)
1.背景
断点回归被认为是局部的随机实验,因此随机推断的方法也可以适用于断点回归,但原则上需要使用断点 (cutoff) 附近的观测值。另一方面,经典的断点回归需要较大的样本量,因为无论是参数估计还是非参数估计,均要求分配变量的密度在断点处是连续的,并且做非参数估计时,使用局部多项式做非参数统计推断,也依靠了大样本渐进理论。这就导致了如果带宽过小或者数据集本身就不大,平滑性检验通不过或者估计效果会变得不好的问题。
为了解决样本量有限的问题,美国普林斯顿大学的 Cattano 教授及其合作者于 2016 年开发了一套 rdlocrand Stata 命令包,运用了随机实验的方法来解决有效样本量 (带宽内的样本数量) 过少的问题。
rdlocrand package 包含了四个命令,本文结合 Cattaneo et al. (2015,[PDF]) 关于美国 1994-2010 年参议院选举的样本数据对这四个命令及其功能进行介绍。
准备 :安装需要使用的命令包
ssc install st0435.pkg,from (http://www.stata-journal.com/software/sj16-2/)
2. 有限样本的断点回归
2.1 RDD 适用性检验和最优带宽的选择
Note: Cattaneo et al. (2015) 使用的参议院选举数据和 David S. Lee (2007,[PDF])使用选举数据在样本的时间段和变量选择上有区别,另外对"在位优势"的定义也不同,David S. Lee 认为 t 期胜出选票的份额对 t+1 期的选举结果有正向影响说明存在"在位优势",而 Cattaneo et al. 则把 "在位优势" 定义为 t 期对 t+2 期的影响。
rdwinselect 命令有两个作用,(1) 利用前定变量(除配置变量以外的其他解释变量) 做 RDD 适用性检验; (2) 在适用性条件被满足的前提下,挑选最优带宽,适用于有限样本和大样本。基本的语法格式如下:
rdwinselect runvar [covariates] [if] [in], [, options]
其中,主要选项为:
-
runvar: 分配变量 -
covariates: 协变量 -
cutoff(): 分配变量临界值, 默认为 c(0) -
obsmin(): 设定左、右带宽包括最少的观测值的个数 -
wmin(): 设定模型带宽长度的最小临界值 -
wstep: 设定模型每次带宽增加的长度 -
nwindows: 设定带宽的个数 -
approximate: 使用大样本渐进理论,默认基于随机推断 -
p(): 结果变量修正模型的阶数,默认 p(0) -
plot: 画出协变量检验的最小 p 值图 -
reps(): 随机试验重复的次数,默认 reps(1000)
命令的使用
.sysuse rdlocrand_senate, clear //调用数据
.global covariates presdemvoteshlag1 population demvoteshlag1 demvoteshlag2 ///
.demwinprv1 demwinprv2 dopen dmidterm //把分配变量以外的所有解释变量设为全局变量 covariates
.rdwinselect demmv $covariates, cutoff(0) //为RD回归选择带宽, demmv是分配变量,代表民主党超过最大对手党派的投票份额(单位:%)
*----------使用 rdwinselect 命令 table1 ----------------------
Window selection for RD under local randomization
Cutoff c = 0.00 | Left of c Right of c Number of obs = 1390
------------------+----------------------- Order of poly = 0
Number of obs | 640 750 Kernel type = uniform
1st percentile | 6 7 Reps = 1000
5th percentile | 32 37 Testing method = rdrandinf
10th percentile | 64 75 Balance test = ttest
20th percentile | 128 150
| Bal. test Var. name Bin. test
Window length /2 | p-value (min p-value) p-value Obs=c
------------------+-------------------------------------------------------------
0.529 | 0.210 demvoteshlag2 0.327 10 16
0.733 | 0.262 dopen 0.200 15 24
0.937 | 0.132 dopen 0.126 16 27
1.141 | 0.044 dopen 0.161 20 31
1.346 | 0.229 dmidterm 0.382 28 36
1.550 | 0.102 dmidterm 0.728 35 39
1.754 | 0.075 dmidterm 0.747 41 45
1.958 | 0.046 dmidterm 0.602 43 49
2.163 | 0.075 dmidterm 0.480 45 53
2.367 | 0.132 dopen 0.637 53 59
Variable used in binomial test (running variable): demmv
Covariates used in balance test: presdemvoteshlag1 population demvoteshlag1 demv
> oteshlag2 demwinprv1 demwinprv2 dopen dmidterm
Recommended window is [-.733; .733] with 39 observations (15 below, 24 above).
解读:rdwinselect 命令推荐的最优窗口是 [-.733; .733], 带宽为 0.733 - (-0.733) = 1.467,断点左右两边观测值个数分别为 15 和 24.
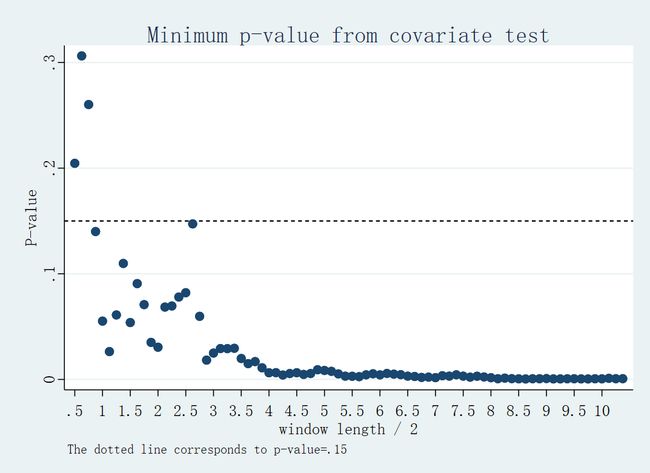
*----------使用 rdwinselect 命令 figure1 ----------------------
.quietly rdwinselect demmv $covariates, wmin(.5) wstep(.125) ///
nwin(80) approximate plot //quietly 表示安静地执行命令不显示结果,只出现图
解读:协变量检验从带宽窗口 [0.5; 0.5] 开始以 0.125 的长度依次增长,可以看出第三个带宽窗口 [0.75, 0.75] 的最小 p 值超过了0.15 线,是符合协变量检验的最优带宽, 这和前面推荐的带宽窗口 [-.733; .733] 非常接近。
连享会计量方法专题……,https://gitee.com/arlionn/Course
2.2 断点回归估计
rdrandinf 命令运用随机推断,对断点回归进行估计,基本的语法格式如下:
rdrandinf outvar runvar [if] [in], [, options]
其中,主要选项为:
-
runvar: 分配变量 -
covariates: 协变量 -
cutoff(): 断点,分配变量临界值, 默认为 c(0) -
wl(): 设定带宽窗口的左边界 -
wr(): 设定带宽窗口的右边界 -
covariates: 协变量 -
kernel: 选择核函数, uniform (均匀核,默认), triangular (三角核), epanechnikov(二次核) -
fuzzy(): 设定模糊断点回归中的内生处理变量
命令的使用
*----------使用 rdrandinf 命令 table2 ----------------------
.rdrandinf demvoteshfor2 demmv, wl(-.75) wr(.75) //处理效应估计,设定带宽为 [0.75; 0.75]
//变量 demvoteshfor2 为结果变量,即 t+2 期的民主党获得投票份额
Selected window = [-.75 ; .75]
Running randomization-based test...
Cutoff c = 0.00 | Left of c Right of c Number of obs = 1390
------------------+----------------------- Order of poly = 0
Number of obs| 595 702 Kernel type = uniform
Eff. Number of obs| 15 22 Reps = 1000
Mean of outcome| 42.808 52.497 Window = set by user
S.D. of outcome| 7.042 7.742 H0: tau = 0.000
Window| -0.750 0.750 Randomization = fixed margins
Outcome: demvoteshfor2. Running variable: demmv.
--------------------------------------------------------------------------------
| Finite sample Large sample
| --------------- -------------------------------
Statistic| T P>|T| P>|T| Power vs d = 3.52
------------------+-------------------------------------------------------------
Diff. in means| 9.689 0.000 0.000 0.300
--------------------------------------------------------------------------------
解读:处理效应为 9.689, 表明民主党于 t 期控制参议院导致了民主党于 t+2 期获得投票份额在断点提高了约 10%, 在 1% 的显著性水平下显著。 Finite sample 下面的 p 值是基于随机检验的结果,而 large sample 下面的 p 值则基于渐进分布理论。
2.3 敏感性分析 (一)
rdsensitivity 命令分析了对于不同的带宽, 处理效应估计值对应的 p 值和置信区间的敏感性,基本语法如下:
rdsensitivity outvar runvar [if] [in], [, options]
其中,主要选项为:
-
outvar: 结果变量 -
runvar: 分配变量 -
covariates: 协变量 -
cutoff(): 断点,分配变量临界值, 默认为 c(0) -
wlist: 设定被估计带宽长度的范围 -
tlist(): 处理效应估计值的范围(整数) -
saving(filename): 保存敏感性分析的等高线图 -
nodots: 删除重复的点 -
nodraw: 删除等高线 -
verbose: 输出 p 值的矩阵结果 -
reps: 随机试验重复的次数,默认 reps(1000)
命令的使用
*----------使用 rdsensitivity 命令 table3 ----------------------
.rdsensitivity demvoteshfor2 demmv, wlist(.75(.25)2) tlist(0(1)20) nodots verbose
//此命令运行时间较长,要耐心等待
Running randomization-based test...
Randomization-based test complete.
| .75 1 1.25 1.5 1.75 2
-------------+------------------------------------------------------------------
0 | 0 .001 0 0 0 0
1 | 0 .001 0 0 0 0
2 | .001 .001 .002 0 0 0
3 | .013 .004 .003 0 0 0
4 | .03 .009 .007 .002 .001 0
5 | .068 .023 .018 .013 .003 .005
6 | .147 .062 .042 .037 .039 .029
7 | .309 .144 .093 .088 .106 .092
8 | .518 .306 .173 .239 .233 .262
9 | .788 .534 .299 .427 .484 .569
10 | .918 .869 .497 .731 .83 .939
11 | .608 .844 .756 .907 .839 .668
12 | .378 .514 .969 .574 .496 .36
13 | .201 .268 .665 .323 .231 .134
14 | .102 .139 .428 .154 .09 .036
15 | .04 .051 .254 .064 .035 .007
16 | .019 .016 .13 .022 .009 .002
17 | .008 .006 .073 .004 .003 0
18 | .003 0 .032 .001 0 0
19 | .001 0 .01 .001 0 0
20 | 0 0 .002 0 0 0
解读: 列名称(.75 等)表示窗宽; 行名称 (0 等) 表示处理效应值,也是估计的原假设; 矩阵的值代表 p 值。当带宽为 [-.75; 0.75] 时,在 95% 的显著性水平下,处理效应估计值为 5 - 14 不会被拒绝,故认为带宽为 [-.75; 0.75] 对应的处理效应值在 5 到 14 之间。同样地,带宽为 [2; 2] 时,处理效应值为 7 到 13 之间。
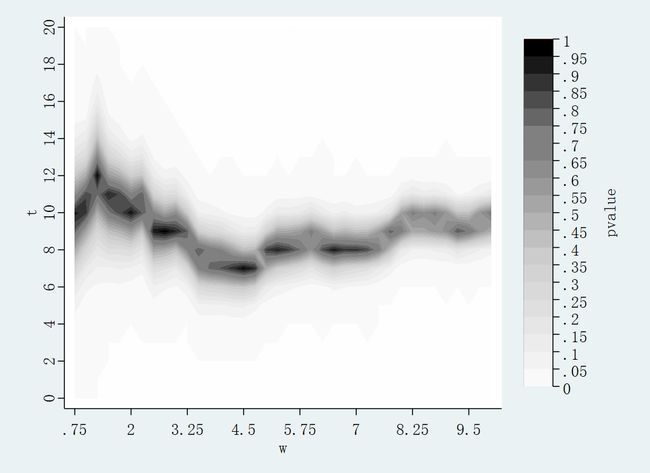
*----------使用 rdsensitivity 命令 figure2 ----------------------
. rdsensitivity demvoteshfor2 demmv, wlist(.75(.25)10) tlist(0(1)20) nodots ///
saving(figure2) //saving()可以允许后面对等高线图进行颜色外观等的修改
. use figure2, clear
. twoway contour pvalue t w, ccuts(0(0.05)1) ccolors(gray*0.01 gray*0.05 ///
gray*0.1 gray*0.15 gray*0.2 gray*0.25 gray*0.3 gray*0.35 ///
gray*0.4 gray*0.5 gray*0.6 gray*0.7 gray*0.8 gray*0.9 gray ///
black*0.5 black*0.6 black*0.7 black*0.8 black*0.9 black) ///
xlabel(.75(1.25)10) ylabel(0(2)20, nogrid) graphregion(fcolor(none))
解读: 由图像也可以看出带宽为 [-.75; 0.75]时,p 值超过 5% 对应的处理效应值在 5 到 14 之间。
2.4 敏感性分析 (二)
rdrbounds 命令是基于 Rosenbaum (2002) 的局部随机化理论,计算不同偏离程度下 p 值变化的范围。
rdrbounds demvoteshfor2 demmv, expgamma(1.5 2 3) wlist(.5 .75 1) reps(1000)
rdrbounds outvar runvar [if] [in], [, options]
其中,主要选项为:
-
runvar: 分配变量 -
cutoff(): 断点,分配变量临界值, 默认为 c(0) -
expgamma(): 需要被估计的 exp(gamma) 的值, 默认为expgamma(1.5 2 2.5 3) -
reps: 随机试验重复的次数,默认reps(500)
命令的使用
*----------使用 rdrbounds 命令 table4 ----------------------
.rdrbounds demvoteshfor2 demmv, expgamma(1.5 2 3) wlist(.5 .75 1) reps(1000)
//此命令运行时间也比较长
Calculating randomization p-values...
w = 0.500 0.750 1.000
--------------------------------------------------------------
Bernoulli p-value| 0.005 0.000 0.000
--------------------------------------------------------------
Running sensitivity analysis...
gamma exp(gamma) w = 0.500 0.750 1.000
--------------------------------------------------------------
0.41 1.50 lower bound| 0.004 0.000 0.000
upper bound| 0.024 0.005 0.002
-----------------------------+--------------------------------
0.69 2.00 lower bound| 0.005 0.000 0.000
upper bound| 0.052 0.025 0.008
-----------------------------+--------------------------------
1.10 3.00 lower bound| 0.005 0.000 0.000
upper bound| 0.194 0.145 0.058
--------------------------------------------------------------
解读: rdrbounds 命令的结果分为两部分,第一个是每个带宽对应 Bernoulli trials 的 p 值, 第二个是在不同的 Γ 和 窗宽下,p 值大小临界值的距离,如果 p 值大小临界值的距离越大,说明随机试验偏差推断越敏感。
第二个结果有两种分析方式,(1) 固定窗宽,看随机试验不同的偏离度如何影响 p 值;(2) 固定随机试验的偏离度,看不同的窗宽如何影响 p 值。对于模型推荐的带宽 [-0.75; 0.75], 在各种偏度下结果都较为稳健。
结语
本文主要对 rdlocrand package 的四个命令 rdwinselect rdrandinf rdsensitivity rdrbounds 进行介绍,并通过美国参议院选举的数据来应用这些命令做 RDD 适用性检验和最优带宽的选择、有限样本的RDD 估计, 以及处理效应值和窗宽敏感性分析。
参考文献
[1] Cattaneo M D , Frandsen B R , Titiunik, Rocío. Randomization Inference in the Regression Discontinuity Design: An Application to Party Advantages in the U.S. Senate[J]. Journal of Causal Inference, 2015, 3(1):1-24pdf.
[2] Cattaneo, Matias, D, et al. Inference in regression discontinuity designs under local randomization[J]. The stata journal, 2016pdf.
[3] Lee D S. Randomized experiments from non-random selection in US House elections[J]. Journal of Econometrics, 2008, 142(2): 675-697pdf.
连享会计量方法专题……,https://gitee.com/arlionn/Course
Appendix 本文涉及的 Stata 代码
sysuse rdlocrand_senate, clear //调用数据
global covariates presdemvoteshlag1 population demvoteshlag1 demvoteshlag2 ///
demwinprv1 demwinprv2 dopen dmidterm //把分配变量以外的所有解释变量设为全局变量 covariates
*----------使用 rdwinselect 命令 table1 ----------------------
rdwinselect demmv $covariates, cutoff(0) //为RD回归选择带宽, demmv是分配变量,代表民主党超过最大对手党派的投票份额(单位:%)
*----------使用 rdwinselect 命令 figure1 ----------------------
quietly rdwinselect demmv $covariates, wmin(.5) wstep(.125) ///
nwin(80) approximate plot //quietly 表示安静地执行命令不显示结果,只出现图
*----------使用 rdrandinf 命令 table2 ----------------------
rdrandinf demvoteshfor2 demmv, wl(-.75) wr(.75) //处理效应估计,设定带宽为 [0.75; 0.75]
//变量 demvoteshfor2 为结果变量,即 t+2 期的民主党获得投票份额
*----------使用 rdsensitivity 命令 table3 ----------------------
rdsensitivity demvoteshfor2 demmv, wlist(.75(.25)2) tlist(0(1)20) nodots verbose //命令运行时间较长
*----------使用 rdsensitivity 命令 figure2 ----------------------
rdsensitivity demvoteshfor2 demmv, wlist(.75(.25)10) tlist(0(1)20) nodots ///
saving(figure2) //saving()可以允许后面对等高线图进行颜色外观等的修改
use figure2, clear
twoway contour pvalue t w, ccuts(0(0.05)1) ccolors(gray*0.01 gray*0.05 ///
gray*0.1 gray*0.15 gray*0.2 gray*0.25 gray*0.3 gray*0.35 ///
gray*0.4 gray*0.5 gray*0.6 gray*0.7 gray*0.8 gray*0.9 gray ///
black*0.5 black*0.6 black*0.7 black*0.8 black*0.9 black) ///
xlabel(.75(1.25)10) ylabel(0(2)20, nogrid) graphregion(fcolor(none))
*----------使用 rdrbounds 命令 table4 ----------------------
rdrbounds demvoteshfor2 demmv, expgamma(1.5 2 3) wlist(.5 .75 1) reps(1000)
//此命令运行时间比较长
连享会直播:我的特斯拉—实证研究设计(连玉君主讲)
课程主页:https://gitee.com/arlionn/Live
关于我们
- Stata连享会 由中山大学连玉君老师团队创办,定期分享实证分析经验。
- 欢迎赐稿: 欢迎赐稿至[email protected]。录用稿件达 三篇 以上,即可 免费 获得一期 Stata 现场培训资格。
- 往期精彩推文:
Stata绘图 | 时间序列+面板数据 | Stata资源 | 数据处理+程序 | 回归分析-交乘项-内生性