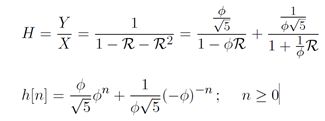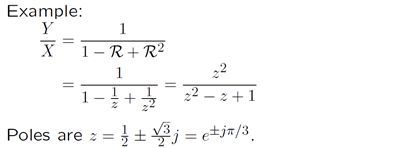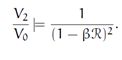1.定义
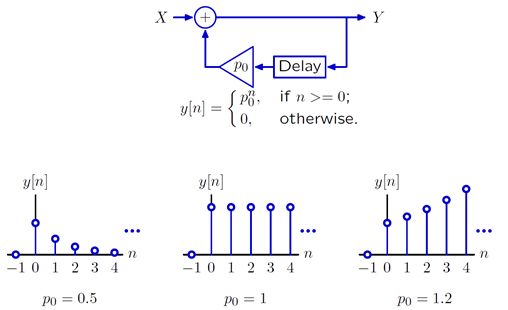
在下列简单的反馈系统中,系统对单位冲击信号的相应为几何级数。
整个系统的性质主要和p0的值有关。P0就是极点(pole)。
PS:若p0小于0时,该系统的冲击响应在正负之间反复震荡。若p0的绝对值小于1,系统的单位冲击响应收敛;若p0的绝对值大于1,则系统的单位冲击响应发散。
2.二阶反馈系统
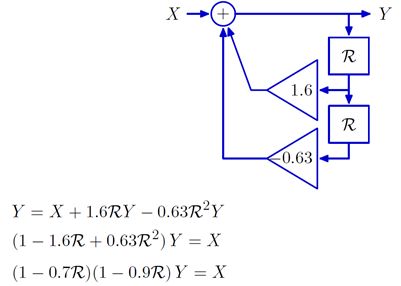
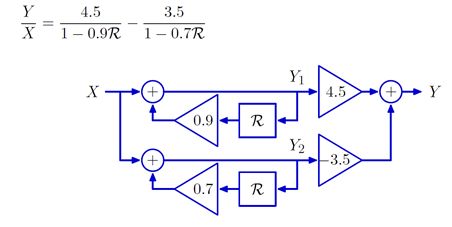
系统差分方程中出现y[n-2]的系统称为二阶系统。下面是个二阶系统的例子。
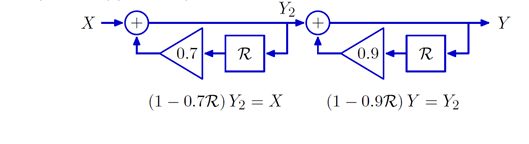
使用R操作符和多项式因式分解的方法,将上述系统等价变形为两个串联的基本一阶反馈系统。
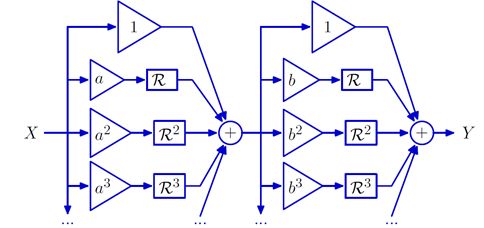
使用无穷级数的相关知识,可将反馈系统转化为一个不包含环的非反馈系统。
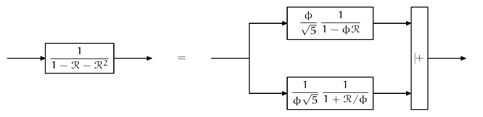
上述二阶系统还能转化为下列"并联"的形式。
二阶系统的极点被定义如下。将2阶系统的系统泛函中的R替换为1/z,然后再找到系统泛函分子等于0的两个根p0和p1。这两个根就是该二阶系统的极点。上述系统的极点为0.7和0.9。
模态(Mode)定义:
一阶系统产生的较为简单的数列就被称为模态。上述二阶系统可分解为两个一阶系统相加。这两个一阶系统就是该二阶系统的模态。
上述例子中,通过对二阶系统的系统泛函使用部分分式的方法,分解为两个分式相加,从而得到了系统的模态。
3. 二阶系统举例
斐波那契系统为二阶系统。其中x[n]为迁入和迁出的兔子。若x[n]只在0处等于1且y[-1]和y[-2]都为0,则系统输出一个斐波那契数列。即下列系统在初始状态为0的情况下的单位冲击响应为斐波那契数列。
通过令R = 1 / z然后去求分母的根的方式,可得到该二阶系统的两个极点,其中一个极点为黄金分割率,另一个为黄金分割比的负倒数。
通过对斐波那契系统的系统泛函进行下列变化,可将该二阶系统转化为两个并行一阶系统的和。从而,可得到斐波那契系统的单位冲击响应为两个几何级数的和。
上述系统的冲击响应就是一个整数数列,就是那个著名斐波那契数列。实际上计算机使用上述公式就可计算得到斐波那契数列,就不需要使用算法课上所使用的迭代方法了。
从模态的角度看,我们已经成功的将该系统分解为了两个一阶系统,得到了该二阶系统的两个模态。
4.二阶系统极点为复数的情况
先说结论。即使一个真实的系统的极点为复数,那它的输出必定为实数。计算过程的复数会在得到输出信号的过程中消除掉,最终得到实数输出。此外,由于欧拉公式的存在,两个极点为复数的系统多半和正余弦有关。若一个一阶系统的极点为复数,则这个系统的输出只能是复数,这个系统不是真实的系统,而可能是某个真实系统的一部分。
下面举个例子。
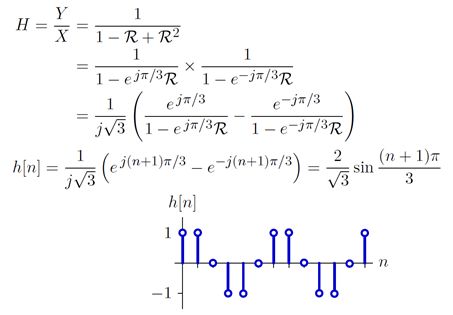
分母等于0的根为两个单位长度的复数。下面使用部分分数对系统泛函进行分解后,可得到系统的单位从事响应。
上述系统的单位冲击响应本质为对正弦函数的采样。
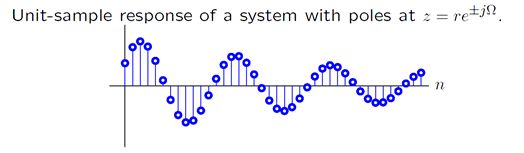
若二阶系统的极点有下列形式,则系统的单位冲击响应为对指数衰减的正弦函数的采样。
真实的二阶系统通过模态分解后可能得到两个复数系统,这两个系统相互作用的结果使得任意实数输入都会得到实数输出。
5.特殊情况:两个相同的一阶系统的串联
将两个极点都为beta的一阶系统串联形成的二阶系统的系统泛函如下
该二阶系统的有两个相等的极点——beta。该系统对应的单位冲击响应为
![]()
该二阶系统的的响应数列不在只是单纯的多个几何序列的和,而是一个几何序列乘以一个n的一次线性表达式。
可验证将三个极点都为beta的一阶系统串联起来的三阶系统的单位冲击响应为一个n的二次表达式乘以一个几何序列。