线性回归(Linear Regression)定义:是一种通过对样本特征进行线性组合来进行预测的线性模型,其目的是找到一条直线或者一个平面或者更高维的超平面,使得预测值与真实值之间的误差最小。
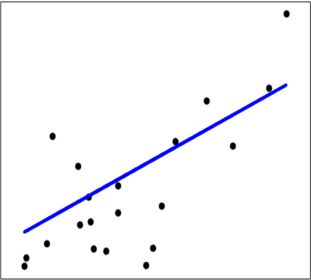
图1:一维数据,线性拟合模型
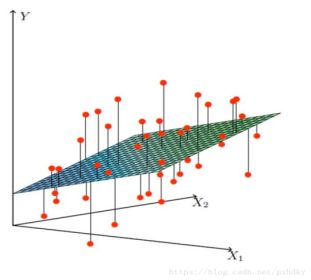
图2:二维数据,平面拟合模型
API文档
sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
下面我们将对线性回归算法中的参数做逐一说明:
'fit_intercept':布尔值,True or False作为可选项,默认为True。意思是是否返回线性回归函数的截距。
'normalize':布尔值,True or False作为可选项,默认为False。意思是是否对样本数据做标准化处理((每一个样本数据-均值)/标准差)。如果fit_interceptr = False,normalize = True,那么在对样本进行训练之前,必须做标准化处理。
'copy_X':布尔值,True or False作为可选项,默认为True。True意味着样本X将被复制,False意味着样本X是被重新写入的。
'n_jobs':整数值,意思是运算时所使用的处理器数量。n_jobs = 1,使用一个处理器单元,n_jobs = -1,使用所有处理器单元。
应用案例演示
下面以sklearn自带的数据集boston房价数据集为例,来使用线性回归算法对未知样本进行房价预测。
[boston房价数据集]https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_boston.html
可以点击这个链接查看下该数据集的简单介绍,下面我们做一下简单的代码示例。
#导入接下来要使用的库
import numpy as np
from sklearn import datasets
from sklearn.linearn_model import LinearRegression
from sklearn.model_selection import train_test_split
#导入数据集
boston = datasets.load_boston()
#获取特征
X = boston.data
#获取标签值
y = boston.target
#数据切分
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)
#导入线性回归模型
lr = LinearRegression()
#使用训练集对模型进行训练
lr.fit(X_train,y_train)
lr.predict(X_test[:10,:])
array([24.9357079 , 23.75163164, 29.32638296, 11.97534566, 21.37272478,
19.19148525, 20.5717479 , 21.21154015, 19.04572003, 20.35463238])
#打印出前10个真实值
print(y_test[:10])
[22.6 50. 23. 8.3 21.2 19.9 20.6 18.7 16.1 18.6]#可以看出预测值在真实值的上下波动。
#评估模型的精度
lr.score(X_test,y_test)
0.6733825506400183#模型的精度只有67%,没有达到我们理想的准确度。
从模型的预测精度可以看出,67%显然无法达到我们的预期。该数据集是一个13维的数据集,有13个变量特征(例如房子的位置,面积,楼层,卧室数量等等)可以对我们的价格产生影响,后期我们可以对原始数据集作进一步的预处理,对特征进行筛选,以使得模型能更好的拟合我们的数据。
模型的属性
针对以上数据集,我们得出线性模型类似于这样:y = a1 * X1 + a2 * X2 +······+ a13 * X13 + b,
其中a1,a2······a13是我们数据集中13个变量特征的权重参数,b是常数项。现我们可以应用模型的属性得出权重参数与常数项。
#权重参数
lr.coef_
array([-1.21310401e-01, 4.44664254e-02, 1.13416945e-02, 2.51124642e+00,
-1.62312529e+01, 3.85906801e+00, -9.98516565e-03, -1.50026956e+00,
2.42143466e-01, -1.10716124e-02, -1.01775264e+00, 6.81446545e-03,
-4.86738066e-01])
#常数项
lr.intercept_
37.93710774183296
lr算法的优缺点
优点:
结果具有很好的可解释性,权重参数很清晰的体现了各特征在结果预测中所起的作用。
缺点:
对非线性数据拟合不好。