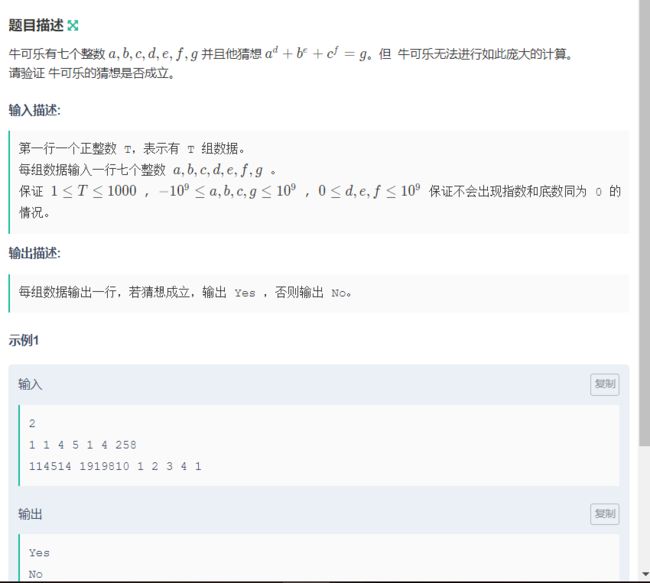
雷比较多,需要一个一个踩。
A : 做游戏
考察点 : 签到题,是否细心(就是看你能否跳过坑)
坑点 : 注意都用 long long 数据类型(两个数相加 可能也会爆 int 哦,刚开始就 卡在这了)Code:
#include
#include
using namespace std;
typedef long long LL;
LL a,b,c,x,y,z;
LL res = 0;
int main(void) {
scanf("%lld%lld%lld",&a,&b,&c); // long long
scanf("%lld%lld%lld",&x,&y,&z);
res += min(a,y) + min(b,z) + min(c,x);
cout << res << endl;
return 0;
} B : 排数字
考察点 : 字符串,及特判,对某些名词的概念理解
坑点 : 一定要认真读题,认真读题,题中是子串,而不是子序列,子串是连续的,所以 616一定是连续的,比如 61616就是
两个,而不是三个,只统计616,不用统计61616,也不能随意组合,因为是连续的。Code :
#include C:算概率
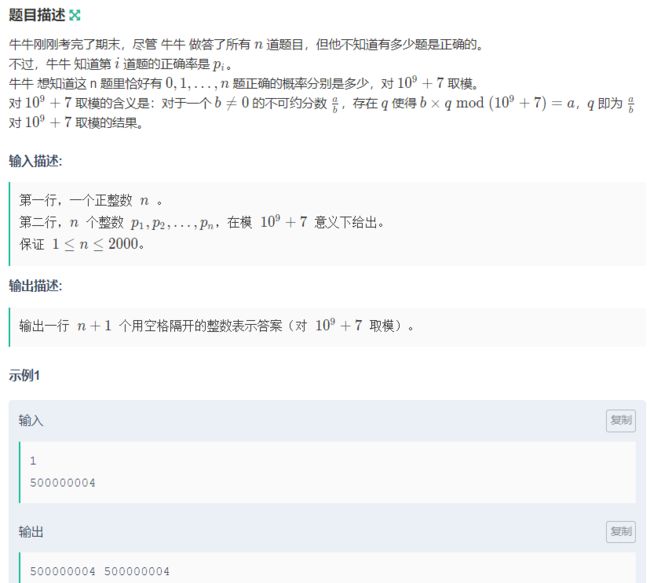
考察点 : dp ,概率, 同余定理,模运算下的意义
坑点 : long long ,模的数一般都比较大,所以用 long long 比较保险
最好 + 上一个 MOD 防止出现 负数
析题得侃 :
遇到 DP 就歇菜,只能慢慢啃了。
DP 最容易的是只需要一个转移方程,最艰难的就是找到这个转移方程。(一般是题最后问的是什么我们就设什么)
假设 DP[i][j] 表示前 i 道题中 恰好做对 j 道的概率是多少,下一步就会出现两种情况:
1、第 i 道是对的,那么 dp[i][j] = dp[i - 1][j - 1] * p[i];
2、第 i 道是错的,那么 dp[i][j] = dp[i - 1][j] * (1 - p[i]); // 1 - p[i] 是做错的概率
所以 dp[i][j] = dp[i - 1][j - 1] * p[i] + dp[i - 1][j] * (1 - p[i]);Code:
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int MOD = 1e9 + 7;
const int maxn = 2020;
LL dp[maxn][maxn],p[maxn];
int n;
int main(void) {
scanf("%d",&n);
for(int i = 1; i <= n; i ++) {
scanf("%lld",&p[i]);
}
dp[0][0] = 1;
for(int i = 1; i <= n; i ++) { // 前 i 道中 0 道正确的概率也就是没有正确的概率(初始化,为后面做准备)
dp[i][0] = dp[i - 1][0] * (MOD + 1 - p[i]) % MOD; // + 1是为了防止取到负数 (同余定理)
}
for(int i = 1; i <= n; i ++) {
for(int j = 1; j <= i; j ++) {
dp[i][j] =( (dp[i - 1][j - 1] * p[i]) % MOD + dp[i - 1][j] * (MOD + 1 - p[i]) ) % MOD; // 单个模跟 + 括号 模整体是不一样的
}
}
for(int i = 0; i <= n; i ++ ) {
cout << dp[n][i] << ' ';
}
return 0;
} D : 数三角
考察点 : 数学知识,动手能力
坑点 : 多画画就都看出来了,三点共线的一定无法组成三角形,需要我们进行特判(太坑了)
平面内任意三个点都可以组成一个三角形,只有是线段是我们才会用三角形定理去判断。析题得侃 :
这道题都能看出来,但能做对还是不太容易的,尤其对于像我这种渣渣来说,就是动手能力太差,其实看到这道题就应该先想想
有哪些地方需要特判的(三点共线卡了将近半个小时,最后还是从别人那里听来的,太不容易了)。Code :
#include E : 拿物品

考察点 :数论,思维
坑点 : 不同的两个数交换位置也算一组(哈哈哈哈哈,这也可以,服了,还是想的不够周到)
析题得侃:
乍一看,数论呀,直接跳过,结束后看题解,真easy。(还是能力不济)
我们需要将原来的式子简化一下,然后缩减范围,就像我们之前学的,遇到根号开根号,然后观察这个式子的性质。Code:
#include F : 拿物品

考察点: 贪心(邻项交换),排序
坑点 : 错误的贪心思想,哪个属性的值大就选哪个,这个并不是最优结果.
eg: a : 2 200
b : 1000 50
如果我们按照上述贪心思想,先对 a 排序取最大的显然不是最优的。
析题得侃: 这种类型是贪心得一种典型类型 : 邻项交换得原则(相邻得两个交换并不会影响其他得值,前提是 两个数得属性整体相加,
也有可能是整体相乘再排序,这样会得到一个最优得结果)(最可惜的是我前几天刚做过一道类似得题目,但是当时没有总结
惨痛得教训,学到得知识一定要及时整理和复习)相关题型:
耍杂技的牛
国王游戏
Code:
#include G : 判正误
考察点 : 快速幂,取模
坑点 : 换几个模试试 MOD 1e9 + 7 有可能过不了, MOD % 1e9 + 8 就过了(哈哈哈哈,服了)析题得侃 :
这么大次方,肯定选 快速幂,又有这么大的数,得取模呀(虽然题目中没有这样要求,但是我们可以这样尝试一下)Code :
#include H : 施魔法
考察点 : DP,思维,推理
坑点 : 遇到 DP 就凉凉Code : 待补(目前看题解还没搞透彻)
I :建通道

考察点 : Tree,位运算,思维
坑点 : 能想到就完事了,去重
析题得侃 :
初看这道题,这不是最小生成树的模板吗,但是定睛一看,发现没边权呀,这不是歇菜了。
后来在一位大佬的指导下,终于将其看懂,理解,并且AC。
这道题还是蛮有特点的 : 求 异或(二进制位下相同 取 0 不同取 1),而且还是 lowbit(异或)下的最小值。
我们知道两个不同的数在二进制下一定存在某一位是不同的(一个是 0 ,一个是 1),那么在我们的所有数中,也
一定存在在更低的位置(靠右的)有两个不同的二进制位,我们将这两个不同的二进制位取异或,得到的一定是 1 ,
再lowbit那么这个肯定就是这两个点的之间的最小边权(我们说了是在最低的位置),然后我们知道所有数都可以
通过二进制表示出来,那么这个数的二进制位与最低位的同一个位置的数一定不是 0 就是 1 ,我们知道最小边
权的一端存在一个 0 ,另一端存在一个 1,那么我们只要让这个数的的该二进制位是 0 就和 1 相连,是 1 就和
0 相连,因为异或。到这里,就都是最小边权了,最后的最小花费就是 (m - 1) * 最小边权。
lowbit(x) = x & (-x);
lowbit () 取得的值 1,2,4,8........(所以最多只需要枚举30次)(可以写个数的二进制位模拟一下)#include J :求函数

考察点 : 线段树的基本操作
坑点 : 代码比较长,注意细节

析题得侃 :
线段树我们肯定要找到需要合并得东西,例如求区间和我们需要父节点存储得是两个数得和,求区间最大值我们需要
往上推送的是两个数的最大值,那这个需要往上pushup的是啥呢 ?
我们发现 : f(L) = kL + b
所以 f(L1) = f(f(L)) = k(k * L + b) + b = k * k * L + k * b + b;
所以我们pushup 的应该是 k * k + k * b + b (K, b 都是已知的)(可以分成两部分)#include
#include
#include
#include
#include
#define int long long
using namespace std;
const int maxn = 2e5 + 10;
const int MOD = 1e9 + 7;
typedef long long LL;
struct node {
int l,r,k,b;
} tree[maxn << 2];
int a[maxn],b[maxn];
int n,m;
int ans,res;
signed main(void) {
void build(int u,int l,int r);
void update(int u,int x);
void query(int u,int l,int r);
scanf("%lld%lld",&n,&m);
for(int i = 1; i <= n; i ++) {
scanf("%lld",&a[i]);
}
for(int i = 1; i <= n; i ++) {
scanf("%lld",&b[i]);
}
build(1,1,n);
while(m --) {
int op,pos,l,r;
scanf("%lld",&op);
if(op == 1) {
scanf("%lld",&pos);
update(1,pos);
} else {
ans = 0,res = 1; // 这里我们设置成全局变量,就不用最后去合并了,最好还是合并吧,这样写总感觉有点不妥
scanf("%lld%lld",&l,&r);
query(1,l,r);
cout << (ans + res) % MOD << endl;
}
}
return 0;
}
void pushup(int u) {
tree[u].k = (tree[u << 1].k * tree[u << 1 | 1].k) % MOD;
tree[u].b = (tree[u << 1 | 1].k * tree[u << 1].b + tree[u << 1 | 1].b ) % MOD;
return ;
}
void build(int u,int l,int r) {
if(l == r) {
tree[u].l = l;
tree[u].r = r;
tree[u].k = a[l];
tree[u].b = b[l];
return ;
}
tree[u].l = l;
tree[u].r = r;
int mid = l + r >> 1;
build(u << 1,l,mid);
build(u << 1 | 1,mid + 1,r);
pushup(u);
return ;
}
void update(int u,int x) {
if(tree[u].l == tree[u].r) {
scanf("%lld%lld",&tree[u].k,&tree[u].b);
return ;
}
int mid = tree[u].l + tree[u].r >> 1;
if(x <= mid) update(u << 1,x);
else update(u << 1 | 1,x);
pushup(u);
}
void query(int u,int l,int r) {
if(tree[u].l >= l && tree[u].r <= r) {
res = (res * tree[u].k) % MOD;
ans = (ans * tree[u].k + tree[u].b) % MOD;
return ;
}
int mid = tree[u].l + tree[u].r >> 1;
if(l <= mid) query(u << 1,l,r); // 这里判断条件一定不要写反,写反可能会发生段错误,调了一个多小时,最后还是对照着别人的才看出来
if(r > mid) query(u << 1 | 1,l,r);
return ;
}