There are some animals in a zoo which can be described as a grid with N rows and M columns. Your task is to place some obstacles so that no pairs of animals can reach each other.
Two animals can reach each other if and only if their cells are 4-connected. For example, in Figure 1, the central blue cell can be reached by the four red cells, and cannot be reached by the other four white cells.
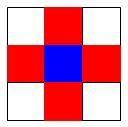
Figure 1
What is more, you must put obstacles in exactly K cells, which are 4-connected and form exactly H holes. Here a hole is defined as a 4-connected part with finitely many open cells while the zoo is placed in an infinite open grid. For example, there are 2 holes (the green and the yellow areas) in Figure 2.

Figure 2
For the following grid with two animals:

Figure 3
If K = 8 and H = 1, one way to separate them is the following:

Figure 4
Figure 5 is illegal because it contains no hole.

Figure 5
Figure 6 is also illegal because the obstacles are not 4-connected.

Figure 6
Given some animals, you are supposed to count the number of different solutions.
Each input file contains one test case. For each case, the first line gives four integers: N, M, K, H (2 ≤ N, M ≤ 6; 1 ≤ K ≤ 12; 0 ≤ H ≤ 2). All the numbers are separated by spaces.
Then N lines follow, each contains M characters, which are either . or O, representing an open cell or an animal, respectively. There will be at least 2 animals.
Output Specification:
For each case, print a single line containing a single integer: the number of solutions.
3 5 8 1
...O.
.O...
.....
Sample Output:
8
1 #include





