实验六
test1
- 利用roots函数求解非线性方程：
解：
%roots函数
%f(x) = x^3-6*x^2-72*x-27
p = [1, -6, -72, -27];
res = roots(p);
res
运行结果
>> test1
res =
12.1229
-5.7345
-0.3884
fzero函数样例运行测试
样例：
%但fzero函数只给出离x0最近的那个根。
%z=fzero('fname',x0,tol,trace)
%画出函数图像，对该函数有个大概的印象
t=-10:0.01:10;
y=sin(t).^2.*exp(-0.1*t)-0.5*abs(t);
plot(t,y)
hold on
plot([-10 10],[0 0],'k');
%从图像我们可以看出大概在x=[-2-1 0 1 2]附近的某个值时，y为零。下面我们就用fzero来具体求出零点。
f=@(t)sin(t).^2.*exp(-0.1*t)-0.5*abs(t)
%第一种方法使用arrayfun
x=[-2 -1 0 1 2];
%arrayfun(@(x)fzero(f,x),x)
%第二种方法，分别带入
[x1 y]=fzero(f,-2)
[x2,y]=fzero(f,-1)
[x3,y]=fzero(f,0)
[x4,y]=fzero(f,1)
[x5,y]=fzero(f,2)
arrayfun(@(x)fzero(f,x),x)
运行结果：
>>test2
f =
包含以下值的 function_handle:
@(t)sin(t).^2.*exp(-0.1*t)-0.5*abs(t)
x1 =
-2.0074
y =
2.2204e-16
x2 =
-0.5198
y =
-5.5511e-17
x3 =
0
y =
0
x4 =
0.5993
y =
0
x5 =
1.6738
y =
2.2204e-16
ans =
-2.0074 -0.5198 0 0.5993 1.6738
test2运行结果图
- 画出以下非线性函数，利用fzero函数求解零点：
解：
test2_1
clear;
%单根求解
x=-20:0.01:20;
y=x.^7+2*x.^5+1;
plot(x,y)
hold on
plot([-20 20],[0 0],'k');
f=@(x)x^7+2*x^5+1;
res = fzero(f,-0.8);
res
%%%%%%%%%%%%
>> test2_1
res =
-0.8214
运行结果图1
001.jpg
test2_2
clear;
%多重根求解
a=0.15;
b=0.5;
t=-20:0.01:20;
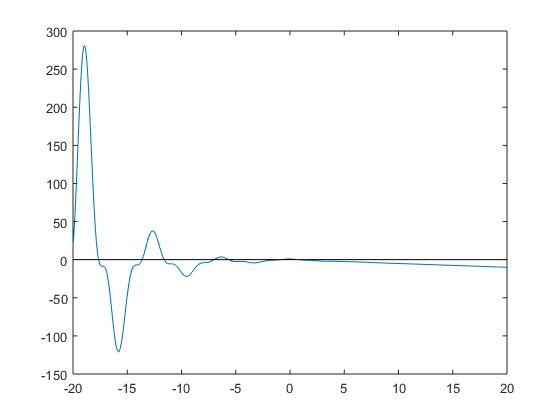
y = cos(t).^3.*exp(-2*a*t)-b*abs(t);
plot(t,y)
hold on
plot([-20 20],[0 0],'k');
f=@(t)cos(t).^3.*exp(-2*a*t)-b*abs(t);
res = fzero(f,-0.8);
res
%%%%%%%%%
>> test2_2
res =
-0.8177
运行结果2
002.jpg
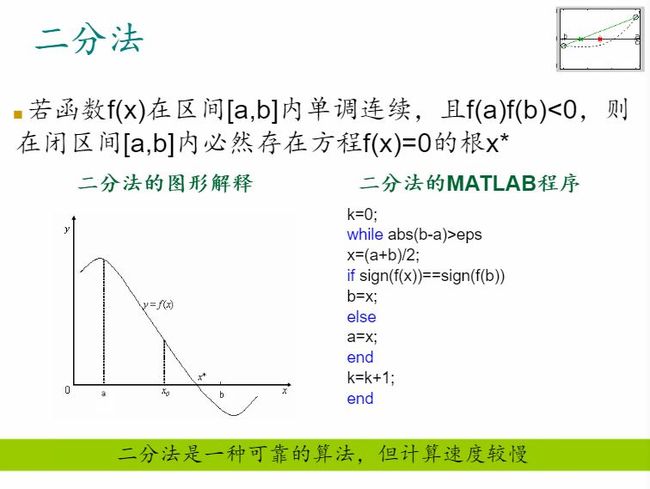
二分法
test2.JPG
多重根求解
test2_2.jpg
fzero不能获得多项式的多重根，尤其是复数根；而roots函数求解可以获得所有根。
fzero求解方程x2.*exp(-x2)=0.2在区间[-2,2]的根？
fzero(@(x)x.^2.*exp(-x.^2)-0.2,0)
https://blog.csdn.net/lqhbupt/article/details/18009015
样例：
>> syms x
>> solve(x^7+2*x^5+1)
ans =
-0.82138342524233730783180723576101
- 0.3533142445050346017251168917277 - 0.84803943068664341373324461904684*i
- 0.3533142445050346017251168917277 + 0.84803943068664341373324461904684*i
0.057709544218893076591497097925659 + 1.4272619559849694123531714767915*i
0.057709544218893076591497097925659 - 1.4272619559849694123531714767915*i
0.70629641290731017904952341168255 - 0.45618391946658911016799825085068*i
0.70629641290731017904952341168255 + 0.45618391946658911016799825085068*i
%%说明：有一个实根
>> f=@(x)x^7+2*x^5+1;fzero(f,-0.8)
ans =
-0.821383425242337
4.JPG
- 利用fsolve函数求解非线性方程组：
解：
function q=myfun(p)
x=p(1);
y=p(2);
q(1)=2*x^3-y-exp(-x);
q(2)=-x+2*y-exp(-y);
end
%初始值设置x0=1;y0=1;
%%%%%%%%%%%运行结果
>> x=fsolve('myfun',[1,1],optimset('Display','off'));
>> x
x =
0.8211 0.6671
- 利用二分法求解非线性方程并画图检验。
解：
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%函数erfen.m
function [k, x, wuca, yx]=erfen(a, b, abtol)
a(1)=a;
b(1)=b;
ya=fun(a(1));
yb=fun(b(1));
if ya*yb > 0,
disp('please reset a and b!'),return
end
max1=-1+ceil((log(b-a) - log(abtol))/log(2));
%ceil是向正无穷方向取整； abtol是误差;
for k=1:max+1
a;
ya=fun(a);
b;
yb=fun(b);
x=(a+b)/2;
yx=fun(x);
wuca=abs(b-a)/2;
k = k-1;
[k,a,b,x,wuca,ya,yb,yx];
if yx==0
a = x;
b = x;
elseif yx==0
a=x;
b=x;
elseif yb*yx>0
b=x;
yb=yx;
else
a=x;
ya=yx;
end
k=max1;
x;
wuca;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%test4
clear;
%function [k, x, wuca, yx]=erfen(a, b, abtol)
x=-10:0.01:10;
%x=-2:0.01:4;
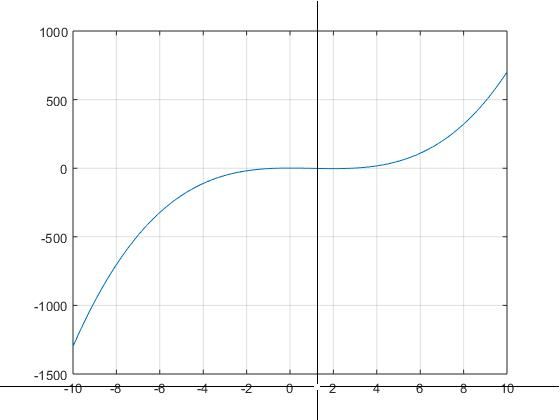
y=(x-1).^3-3*x+2;
%作图
plot(x, y);
%鼠标基准线显示+网格+有报错但能运行
grid,gtext('y=(x-1).^3-3*x+2');
%%%%%%%%%%%%运行结果%%%%%%%%%
函数图像【10:10】
看起来只有一个解
004.jpg
将区间缩小到【-2:4】
004_1.jpg
可以看到，有三个根
%%亲测此代码有毒！！！代码不可用
clear;
%function [k, x, wuca, yx]=erfen(a, b, abtol)
%x=-10:0.01:10;
x_up =2;
x_down = 3;
error = 0.001;
res_down =(x_down-1).^3-3*x_down+2;
res_up = (x_up-1).^3-3*x_up+2;
while(res_down * res_up < 0)
x = 0.5*(x_up + x_down);
res = x^3 - x - 1;
if( res*res_down < 0 )
x_up = x;
else
x_down = x;
end
if( abs(x_up-x_down) < error )
break;
end
end
%作图
%plot(x, y);
%鼠标基准线显示+网格
%grid,gtext('y=(x-1).^3-3*x+2');
result_x = 0.5*(x_up + x_down);
result_x
%%%%%%%%%%%%%%%%%%%%%%%%%%%
运行结果
result_x =
[-2, 0]
-4.8828e-04
[0, 1]
result_x =
4.8828e-04
[2, 3]
result_x =
2.0005
%%亲测此代码有毒！！！代码不可用
用简单迭代法求非线性方程的根 ，取初值，迭代20次，比较观察以下两种迭代格式的结果。
用牛顿法求解非线性方程的根，取以下不同初值，迭代20次。比较观察结果。
用以下各种方法求非线性方程的全部根：
1） 简单迭代法：
2） 牛顿法
3） 弦截法
4） Aitken加速法
5） 抛物线法
6） solve函数
取相同的迭代初始值，比较以上各方法的收敛速度
利用不动点迭代法求解非线性方程组（自定义初值）：
利用牛顿迭代法求解非线性方程组，初值取（1,1）：
用幂法求解下列矩阵的最大特征值以及对应的特征向量，精确到6位数字：
解：
%由圆盘定理且三特征根所在圆盘都不独立，特征根区间为[-14,18]
%不妨设置x =[1,1,1]
format;
A = [-2 1 -2; 9 -2 7; 4 -1 3] %原矩阵
x = [1;1;1]%初始向量
r = 10^(-6)%误差限
m = [max(x)-1,max(x)];
%m1表示mk，m2表示mk+1
while abs(m(1)-m(2)) >= r
x = A*x;
m(1)=m(2);
m(2)=max(abs(x));
x = x./m(2);
end
disp('特征向量是')
x
disp('最大特征值')
value = m(2)
%%%%%%%%%%%%%%运行结果%%%%%%%%
test10
A =
-2 1 -2
9 -2 7
4 -1 3
x =
1
1
1
r =
1.0000e-06
特征向量是
x =
-0.3975
1.0000
0.5394
最大特征值
value =
1.8019