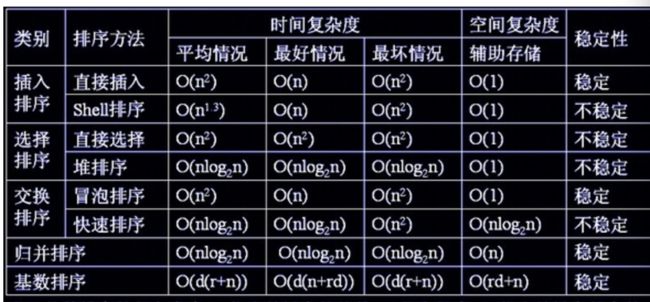
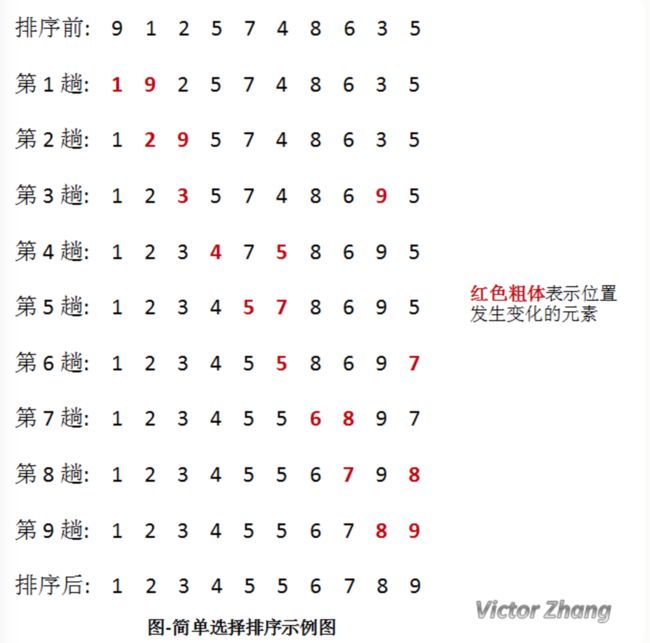
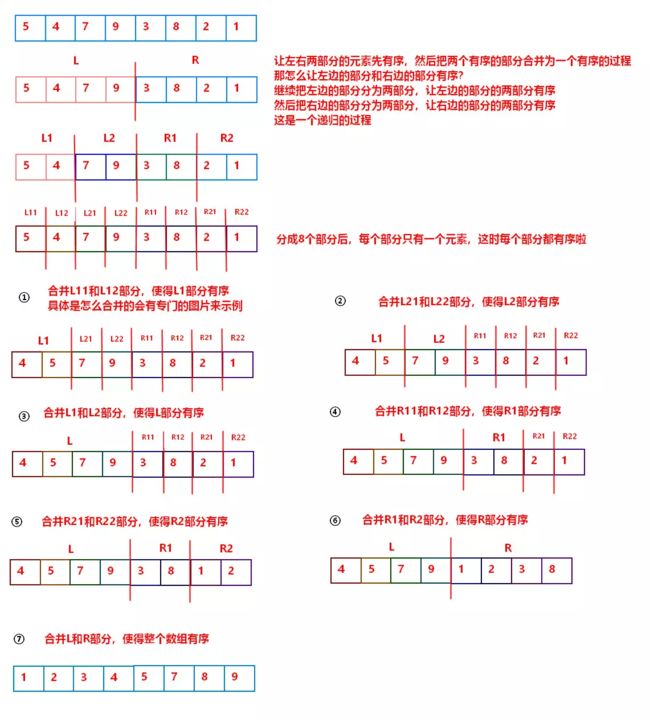
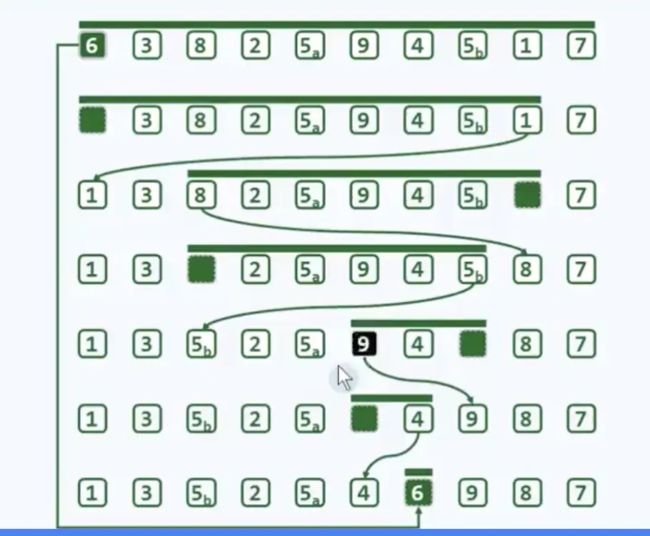
一.选择排序
在待排序的一组数据中,选出最小(最大)的一个数与第一个位置的数交换,然后在剩下的数中,再找最小(最大)的数与第二个位置的数交换位置,依次类推,直到第N-1个元素与第N个元素交换位置,选择排序结束。
import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; import java.util.Comparator; public class Selection { private Selection() { } //排序 public static void sort(Comparable[] a) { int n = a.length; for (int i = 0; i < n; i++) { int min = i; for (int j = i+1; j < n; j++) { if (less(a[j], a[min])) min = j; } exch(a, i, min); assert isSorted(a, 0, i); } assert isSorted(a); } //使用比较器按升序重新排列数组 public static void sort(Object[] a, Comparator comparator) { int n = a.length; for (int i = 0; i < n; i++) { int min = i; for (int j = i+1; j < n; j++) { if (less(comparator, a[j], a[min])) min = j; } exch(a, i, min); assert isSorted(a, comparator, 0, i); } assert isSorted(a, comparator); } //对元素进行比较 private static boolean less(Comparable v, Comparable w) { return v.compareTo(w) < 0; } // 对元素进行比较 private static boolean less(Comparator comparator, Object v, Object w) { return comparator.compare(v, w) < 0; } // 交换两个数据 private static void exch(Object[] a, int i, int j) { Object swap = a[i]; a[i] = a[j]; a[j] = swap; } // 检查数组是否已排序-对调试有用。 private static boolean isSorted(Comparable[] a) { return isSorted(a, 0, a.length - 1); } // 判断从lo到hi的元素是否已经有序 private static boolean isSorted(Comparable[] a, int lo, int hi) { for (int i = lo + 1; i <= hi; i++) if (less(a[i], a[i-1])) return false; return true; } private static boolean isSorted(Object[] a, Comparator comparator) { return isSorted(a, comparator, 0, a.length - 1); } private static boolean isSorted(Object[] a, Comparator comparator, int lo, int hi) { for (int i = lo + 1; i <= hi; i++) if (less(comparator, a[i], a[i-1])) return false; return true; } //输出元素 private static void show(Comparable[] a) { for (int i = 0; i < a.length; i++) { StdOut.println(a[i]); } } public static void main(String[] args) { String[] a = StdIn.readAllStrings(); Selection.sort(a); show(a); } }
二.插入排序
将一个记录插入到已排好序的序列中,从而得到一个新的有序序列(将序列的第一个数据看成是一个有序的子序列,然后从第二个记录逐个向该有序的子序列进行有序的插入,直至整个序列有序)
package sort; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; import java.util.Comparator; public class Insertion { private Insertion() { } public static void sort(Comparable[] a) { int n = a.length; for (int i = 1; i < n; i++) { for (int j = i; j > 0 && less(a[j], a[j-1]); j--) { exch(a, j, j-1); } assert isSorted(a, 0, i); } assert isSorted(a); } //对lo到hi的元素进行排序 public static void sort(Comparable[] a, int lo, int hi) { for (int i = lo + 1; i < hi; i++) { for (int j = i; j > lo && less(a[j], a[j-1]); j--) { exch(a, j, j-1); } } assert isSorted(a, lo, hi); } //使用比较器按升序重新排列数组 public static void sort(Object[] a, Comparator comparator) { int n = a.length; for (int i = 1; i < n; i++) { for (int j = i; j > 0 && less(a[j], a[j-1], comparator); j--) { exch(a, j, j-1); } assert isSorted(a, 0, i, comparator); } assert isSorted(a, comparator); } public static void sort(Object[] a, int lo, int hi, Comparator comparator) { for (int i = lo + 1; i < hi; i++) { for (int j = i; j > lo && less(a[j], a[j-1], comparator); j--) { exch(a, j, j-1); } } assert isSorted(a, lo, hi, comparator); } public static int[] indexSort(Comparable[] a) { int n = a.length; int[] index = new int[n]; for (int i = 0; i < n; i++) index[i] = i; for (int i = 1; i < n; i++) for (int j = i; j > 0 && less(a[index[j]], a[index[j-1]]); j--) exch(index, j, j-1); return index; } //对元素进行比较 private static boolean less(Comparable v, Comparable w) { return v.compareTo(w) < 0; } private static boolean less(Object v, Object w, Comparator comparator) { return comparator.compare(v, w) < 0; } // 交换两个数据 private static void exch(Object[] a, int i, int j) { Object swap = a[i]; a[i] = a[j]; a[j] = swap; } private static void exch(int[] a, int i, int j) { int swap = a[i]; a[i] = a[j]; a[j] = swap; } // 检查数组是否已排序-对调试有用。 private static boolean isSorted(Comparable[] a) { return isSorted(a, 0, a.length); } private static boolean isSorted(Comparable[] a, int lo, int hi) { for (int i = lo + 1; i < hi; i++) if (less(a[i], a[i-1])) return false; return true; } private static boolean isSorted(Object[] a, Comparator comparator) { return isSorted(a, 0, a.length, comparator); } private static boolean isSorted(Object[] a, int lo, int hi, Comparator comparator) { for (int i = lo + 1; i < hi; i++) if (less(a[i], a[i-1], comparator)) return false; return true; } private static void show(Comparable[] a) { for (int i = 0; i < a.length; i++) { StdOut.println(a[i]); } } public static void main(String[] args) { String[] a = StdIn.readAllStrings(); Insertion.sort(a); show(a); } }
三.希尔排序
希尔排序的思想是使数组中任意间隔为h的元素都是有序的。这样的数组被称为h有序数组。换句话说,一个h有序数组就是h个互相独立的有序数组编制在一起组成的一个数组(如下图)。在进行排序的时候,如果h很大,我们能够将元素移动到很远的地方,为了实现更小的h有序创造方便,用这种方式,对于任意以1结尾的h序列,我们都能够将数组排序,这就是希尔排序。
package sort; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; public class Shell { private Shell() { } public static void sort(Comparable[] a) { int n = a.length; int h = 1; while (h < n/3) h = 3*h + 1; //1, 4, 13, 40, 121, 364, 1093, ... while (h >= 1) { for (int i = h; i < n; i++) { for (int j = i; j >= h && less(a[j], a[j-h]); j -= h) { exch(a, j, j-h); } } assert isHsorted(a, h); h /= 3; } assert isSorted(a); } // 比较两个元素 private static boolean less(Comparable v, Comparable w) { return v.compareTo(w) < 0; } // 交换 a[i] 和 a[j] private static void exch(Object[] a, int i, int j) { Object swap = a[i]; a[i] = a[j]; a[j] = swap; } //判断是否有序 private static boolean isSorted(Comparable[] a) { for (int i = 1; i < a.length; i++) if (less(a[i], a[i-1])) return false; return true; } // 判断从h开始是否有序 private static boolean isHsorted(Comparable[] a, int h) { for (int i = h; i < a.length; i++) if (less(a[i], a[i-h])) return false; return true; } // 输出元素 private static void show(Comparable[] a) { for (int i = 0; i < a.length; i++) { StdOut.println(a[i]); } } public static void main(String[] args) { String[] a = StdIn.readAllStrings(); Shell.sort(a); show(a); } }
四.归并排序
1.自顶向下的归并排序
package sort; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; public class Merge { private Merge() { } //排序函数 public static void sort(Comparable[] a) { Comparable[] aux = new Comparable[a.length]; sort(a, aux, 0, a.length-1); assert isSorted(a); } private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) { if (hi <= lo) return; int mid = lo + (hi - lo) / 2; sort(a, aux, lo, mid); sort(a, aux, mid + 1, hi); merge(a, aux, lo, mid, hi); } private static void sort(Comparable[] a, int[] index, int[] aux, int lo, int hi) { if (hi <= lo) return; int mid = lo + (hi - lo) / 2; sort(a, index, aux, lo, mid); sort(a, index, aux, mid + 1, hi); merge(a, index, aux, lo, mid, hi); } //合并两个有序数组 private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) { // precondition: a[lo .. mid] and a[mid+1 .. hi] are sorted subarrays assert isSorted(a, lo, mid); assert isSorted(a, mid+1, hi); // copy to aux[] for (int k = lo; k <= hi; k++) { aux[k] = a[k]; } // merge back to a[] int i = lo, j = mid+1; for (int k = lo; k <= hi; k++) { if (i > mid) a[k] = aux[j++]; else if (j > hi) a[k] = aux[i++]; else if (less(aux[j], aux[i])) a[k] = aux[j++]; else a[k] = aux[i++]; } // postcondition: a[lo .. hi] is sorted assert isSorted(a, lo, hi); } private static void merge(Comparable[] a, int[] index, int[] aux, int lo, int mid, int hi) { // copy to aux[] for (int k = lo; k <= hi; k++) { aux[k] = index[k]; } // merge back to a[] int i = lo, j = mid+1; for (int k = lo; k <= hi; k++) { if (i > mid) index[k] = aux[j++]; else if (j > hi) index[k] = aux[i++]; else if (less(a[aux[j]], a[aux[i]])) index[k] = aux[j++]; else index[k] = aux[i++]; } } //v < w ? private static boolean less(Comparable v, Comparable w) { return v.compareTo(w) < 0; } //判断数组是否有序 private static boolean isSorted(Comparable[] a) { return isSorted(a, 0, a.length - 1); } private static boolean isSorted(Comparable[] a, int lo, int hi) { for (int i = lo + 1; i <= hi; i++) if (less(a[i], a[i-1])) return false; return true; } public static int[] indexSort(Comparable[] a) { int n = a.length; int[] index = new int[n]; for (int i = 0; i < n; i++) index[i] = i; int[] aux = new int[n]; sort(a, index, aux, 0, n-1); return index; } //输出元素 private static void show(Comparable[] a) { for (int i = 0; i < a.length; i++) { StdOut.println(a[i]); } } public static void main(String[] args) { String[] a = StdIn.readAllStrings(); Merge.sort(a); show(a); } }
2.自底向上的归并排序
package sort; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; public class MergeBU { private MergeBU() { } // stably merge a[lo..mid] with a[mid+1..hi] using aux[lo..hi] private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) { // copy to aux[] for (int k = lo; k <= hi; k++) { aux[k] = a[k]; } // merge back to a[] int i = lo, j = mid+1; for (int k = lo; k <= hi; k++) { if (i > mid) a[k] = aux[j++]; // this copying is unneccessary else if (j > hi) a[k] = aux[i++]; else if (less(aux[j], aux[i])) a[k] = aux[j++]; else a[k] = aux[i++]; } } /** * Rearranges the array in ascending order, using the natural order. * @param a the array to be sorted */ public static void sort(Comparable[] a) { int n = a.length; Comparable[] aux = new Comparable[n]; for (int len = 1; len < n; len *= 2) { for (int lo = 0; lo < n-len; lo += len+len) { int mid = lo+len-1; int hi = Math.min(lo+len+len-1, n-1); merge(a, aux, lo, mid, hi); } } assert isSorted(a); } // is v < w ? private static boolean less(Comparable v, Comparable w) { return v.compareTo(w) < 0; } /*************************************************************************** * Check if array is sorted - useful for debugging. ***************************************************************************/ private static boolean isSorted(Comparable[] a) { for (int i = 1; i < a.length; i++) if (less(a[i], a[i-1])) return false; return true; } // print array to standard output private static void show(Comparable[] a) { for (int i = 0; i < a.length; i++) { StdOut.println(a[i]); } } public static void main(String[] args) { String[] a = StdIn.readAllStrings(); MergeBU.sort(a); show(a); } }
五.快速排序
它的基本思想是:
选择一个基准数,通过一趟排序将要排序的数据分割成独立的两部分;其中一部分的所有数据都比另外一部分的所有数据都要小。然后,再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
1.快速排序
package sort; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; import edu.princeton.cs.algs4.StdRandom; public class Quick { private Quick() { } //使用自然顺序按升序重新排列数组。 public static void sort(Comparable[] a) { StdRandom.shuffle(a); sort(a, 0, a.length - 1); assert isSorted(a); } // 排序 a[lo] 到 a[hi]的元素 private static void sort(Comparable[] a, int lo, int hi) { if (hi <= lo) return; int j = partition(a, lo, hi); sort(a, lo, j-1); sort(a, j+1, hi); assert isSorted(a, lo, hi); } // 分区子阵列a[lo..hi],使a[lo..j-1]<=a[j]<=a[j+1..hi] private static int partition(Comparable[] a, int lo, int hi) { int i = lo; int j = hi + 1; Comparable v = a[lo]; while (true) { // 查找左边需要交换的元素 while (less(a[++i], v)) { if (i == hi) break; } // 查找右边需要交换的元素 while (less(v, a[--j])) { if (j == lo) break; } if (i >= j) break; exch(a, i, j); } exch(a, lo, j); return j; } //重新排列数组,使{@code a[k]}包含第k个最小键; public static Comparable select(Comparable[] a, int k) { if (k < 0 || k >= a.length) { throw new IllegalArgumentException("index is not between 0 and " + a.length + ": " + k); } StdRandom.shuffle(a); int lo = 0, hi = a.length - 1; while (hi > lo) { int i = partition(a, lo, hi); if (i > k) hi = i - 1; else if (i < k) lo = i + 1; else return a[i]; } return a[lo]; } // is v < w ? private static boolean less(Comparable v, Comparable w) { if (v == w) return false; // optimization when reference equals return v.compareTo(w) < 0; } // 交换 a[i] 和 a[j] private static void exch(Object[] a, int i, int j) { Object swap = a[i]; a[i] = a[j]; a[j] = swap; } //判断数组是否有序 private static boolean isSorted(Comparable[] a) { return isSorted(a, 0, a.length - 1); } private static boolean isSorted(Comparable[] a, int lo, int hi) { for (int i = lo + 1; i <= hi; i++) if (less(a[i], a[i-1])) return false; return true; } //输出数组 private static void show(Comparable[] a) { for (int i = 0; i < a.length; i++) { StdOut.println(a[i]); } } public static void main(String[] args) { String[] a = StdIn.readAllStrings(); Quick.sort(a); show(a); assert isSorted(a); StdRandom.shuffle(a); StdOut.println(); for (int i = 0; i < a.length; i++) { String ith = (String) Quick.select(a, i); StdOut.println(ith); } } }
2.三向切分的快速排序
package sort; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; import edu.princeton.cs.algs4.StdRandom; public class Quick3way { private Quick3way() { } public static void sort(Comparable[] a) { StdRandom.shuffle(a); sort(a, 0, a.length - 1); assert isSorted(a); } private static void sort(Comparable[] a, int lo, int hi) { if (hi <= lo) return; int lt = lo, gt = hi; Comparable v = a[lo]; int i = lo + 1; while (i <= gt) { int cmp = a[i].compareTo(v); if (cmp < 0) exch(a, lt++, i++); else if (cmp > 0) exch(a, i, gt--); else i++; } // a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi]. sort(a, lo, lt-1); sort(a, gt+1, hi); assert isSorted(a, lo, hi); } // is v < w ? private static boolean less(Comparable v, Comparable w) { return v.compareTo(w) < 0; } // 交换 a[i] 和 a[j] private static void exch(Object[] a, int i, int j) { Object swap = a[i]; a[i] = a[j]; a[j] = swap; } //判断数组是否有序 private static boolean isSorted(Comparable[] a) { return isSorted(a, 0, a.length - 1); } private static boolean isSorted(Comparable[] a, int lo, int hi) { for (int i = lo + 1; i <= hi; i++) if (less(a[i], a[i-1])) return false; return true; } // 输出数组 private static void show(Comparable[] a) { for (int i = 0; i < a.length; i++) { StdOut.println(a[i]); } } public static void main(String[] args) { String[] a = StdIn.readAllStrings(); Quick3way.sort(a); show(a); } }
六.堆排序
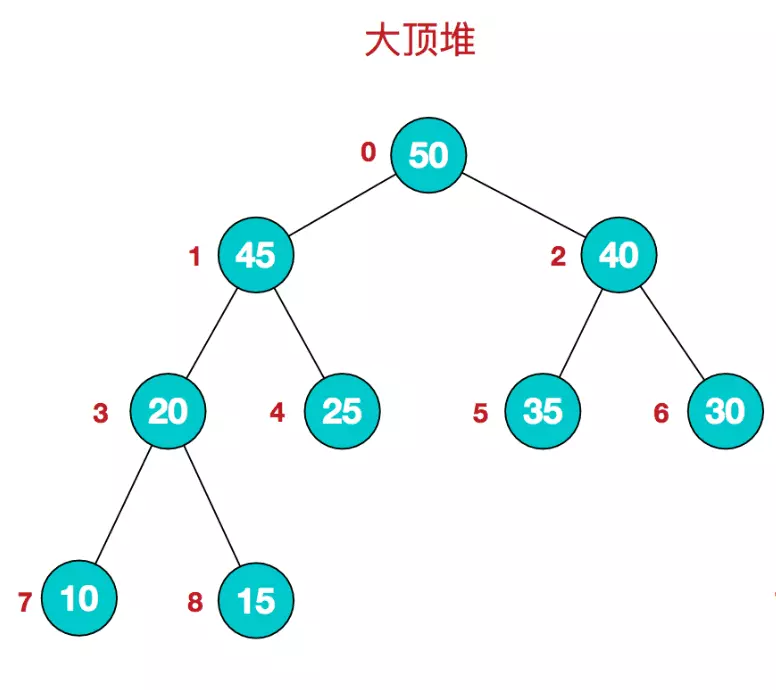
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
大顶堆
小顶堆
package sort; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; public class Heap { private Heap() { } public static void sort(Comparable[] pq) { int n = pq.length; for (int k = n/2; k >= 1; k--) sink(pq, k, n); while (n > 1) { exch(pq, 1, n--); sink(pq, 1, n); } } //下沉 private static void sink(Comparable[] pq, int k, int n) { while (2*k <= n) { int j = 2*k; if (j < n && less(pq, j, j+1)) j++; if (!less(pq, k, j)) break; exch(pq, k, j); k = j; } } //比较 private static boolean less(Comparable[] pq, int i, int j) { return pq[i-1].compareTo(pq[j-1]) < 0; } //交换 private static void exch(Object[] pq, int i, int j) { Object swap = pq[i-1]; pq[i-1] = pq[j-1]; pq[j-1] = swap; } //输出元素 private static void show(Comparable[] a) { for (int i = 0; i < a.length; i++) { StdOut.println(a[i]); } } public static void main(String[] args) { String[] a = StdIn.readAllStrings(); Heap.sort(a); show(a); } }