你知道:
众多病患等待器官移植,肾源匮乏,waiting list应如何抉择,实现最优配置?
选课、择校、集体相亲,要怎样设定规则才能让双方满意?
为什么有些东西要通过拍卖开出售?拍卖有哪几种形式?那种最“好”?
再回答这些问题之前容我介绍一下2012年诺贝尔经济学奖获得者及他们的研究方向。
2012年诺贝尔经济学家获得者是美国经济学家埃尔文·罗斯(Alvin Roth)和罗伊德·沙普利(Lloyd Shapley),他们在稳定配置理论及市场设计实践上作出重要贡献,有效解决如何尽可能恰当地匹配不同的市场主体这一问题。
没错!正是2012年诺贝尔经济学奖新潮理论解决了上述这些有钱也不好使的大问题,让我们梦寐以求的资源得到合乎心意的配置。
日本经济学界翘楚坂井丰贵著作的《合适》,通过可供剖析的实用案例,用深入浅出的表达将诺奖理论讲得清楚透彻,用人人能动的算法,解决实实在在的问题,让我收获了破解谜题的阅读快感。
书中提到的令人惊叹的TTC算法和延迟接受算法是全书的核心。两种算法连小学生都可以很快学会,但是它又能解决经济学领域的疑难问题。如果你沉浸书中,你一定会和我一样惊艳于看上去如此“简单”的方法竟能释放出如此巨大的能量,同时也一定会为经济学家思维的层次感与创造性所折服。
阅读本文时,请稍微耐心一点,一定会让你受益匪浅。
年关将近,很多单身的朋友又要面临新一轮的催婚潮。作为单身贵族的元老,我就以如何找到真命天子,实现婚姻最大稳定性为例,跟大家分享2012年诺奖理论的延迟接受算法,希望给大家有所启发。
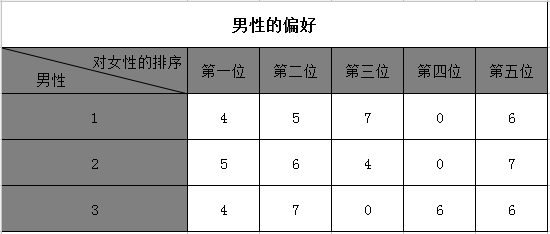
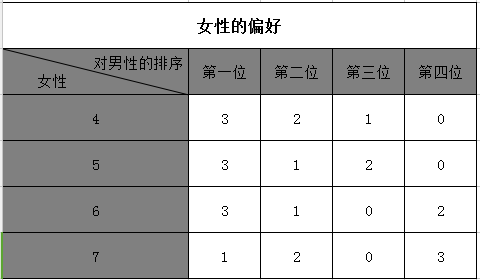
假设有7个人,1到3位“男性”,4到7为“女性”。这里的男性和女性都喜欢异性,0表示“偏好单身”。男性对女性、女性对男性的偏好见下表。
表格的意思是:男性1的偏好顺序是“女性4、女性5、女性7、单身、女性6”,其他人一次类推。大家不妨把自己设想为喜欢牵线搭桥的热心阿姨,这样会更容易理解后面的内容。
首先来看一下在此情况下采用AB轮方式结果会怎样。不允许“一夫多妻”或“一妻多夫”,只考虑一对一组合,称为“一对一”匹配。
A轮(第一轮)
每个男生向自己最喜欢的女性求婚(如果觉得单身好久选择单身,下文同理)。女性在想自己求婚的人中选出自己最喜欢的男性,接受他的求婚。
这里男性1和3向女性4求婚,女性4接受了男性3的求婚;男性2向女性5求婚,女性5接受了他的求婚。最后成功配对:
(3❤4)
(2❤5)
B轮(第二轮)
那么目前还没有配对的有男性1,女性6,女性7。
还没有确定对象的男性向剩下的人里自己最喜欢的女性求婚。女性在向自己求婚的人中选出自己最喜欢的男性,接受他的求婚。在这个例子里,男性1向女性7求婚,女性7接受了他的求婚:
(1❤7)
到此程序结束,女性6单身。
我们来观察这个匹配,可以发现:男性1和女性7成了一对,但他更喜欢女性5,女性5虽然和男性2成了一对,但她更喜欢男性1。
所以这个匹配中男性1和女性5之间可能会发生“私奔”,用TTC算法来说就是“阻止”。作为媒人阿姨要避免这种情况发生,找到更加两情相悦,更加稳定的匹配。
但AB轮方式的缺陷不仅得不到稳定的匹配,还对策略性操作无能为力。
什么是“策略性操作”呢?简单来说,就是有人不诚实,隐瞒自己的异性偏好。
举个例子。
如果男性1采取策略性操作,把排在第一位和第二位的女性颠倒一下,也就是说不按照“4、5、7、0、6”这个真实的偏好顺序而是按照“5、4、7、0、6”这个虚假的偏好顺序求婚,结果会如何呢?
这样,在A轮中男性1和男性2向女性5求婚,女性5会接受男性1的求婚。而男性1比起女性7更喜欢女性5。
所以,男性1通过这样的策略性操作可以使自己找到更满意的配对。
说到这里,那到底存不存在既能防止策略性操作,又能找到稳定匹配的方式呢?
答案是确实存在。这就是我今天要讲的由盖尔和沙普利所创延迟接受算法(Deferred-Acceptance Algorithm)。
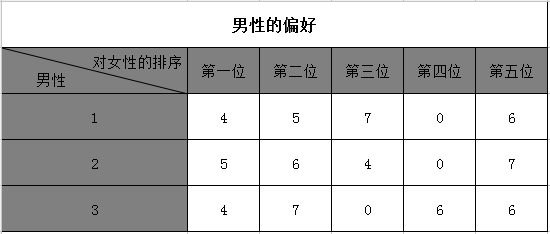
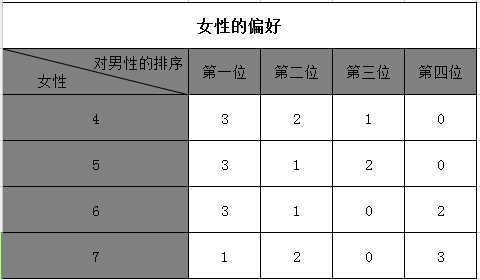
同样是上面的例子,男性对女性、女性对男性的偏好见下表。
延迟接受算法的关键在于合意的要约不是被“接受”,而只是被“保留”,这是其名为“延迟”接受方式的原因。
第一轮
这一轮中,男性1和3向女性4求婚,女性4保留了男性3的求婚,男性1被拒绝;男性2向女性5求婚,女性5保留了他的求婚。
(3❤4)
(2❤5)
第二轮
这一轮中,男性1向女性5求婚,女性5比较了男性1和第一轮中保留求婚的男性2,保留了自己更喜欢男性1,男性2则被拒绝。
(3❤4)
(1❤5)
第三轮
这一轮中,男性2向女性6求婚,女性6选择单身,男性2被拒绝。
第四轮
这一轮中,男性2向女性4求婚,女性4比较了男性2和保留求婚的男性3,继续保留男性3的求婚,男性2被拒绝。
第五轮
最后一轮,对于男性2来说还没有拒绝他的只有女性7,但是觉得与其和他成为情侣还不如单身,最终选择了单身。
到此程序结束,确定了匹配(3❤4)(1❤5),男性2、女性6、女性7单身。
我们来确认一下在这个匹配中不会出现“私奔”。
对于男性1来说,比起和称为一对的女性5,他更喜欢女性4,但是女性4比起男性1更喜欢和她成为一对的男性3。也就是说不会出现包含男性1在内的私奔。
同样,对于女性5来说,比起和她称为一对的男性1,她更喜欢男性3,但是男性3不会和她私奔。因为在这个例子中,男性3和女性4都和自己喜欢的人成了一对,所以这两人不会私奔。
也就是说这个匹配是最稳定的,这个不是个例。盖尔和沙普利证明了无论有几个男女、无论他(她)们的偏好如何,使用延迟接受算法都可以得到稳定的匹配。
同时根据延迟接受算法,我们还可以得出以下结论:
利益一致:对于所有男性来说,男性作为求婚一方所得到的稳定匹配比其他所有稳定匹配都令他们满意。女性同理。
诚实原则:男性作为求婚乙方时,诚实地表面偏好对于男性来说是最有利的。女性同理。
偏僻医院定理:虽然稳定匹配可能会有几个,可是单身的人无论在那个稳定匹配中都是单身。
延迟接受算法,现在广泛应用于实习医生匹配、择校匹配以及从大学的附属高中进入大学的名额分配等诸多情形。
这篇文章只是涉及该书的1/3还不到的内容,其他部分也非常精彩。基于匹配理论,作者深入浅出地介绍了肾源匹配、择校、拍卖等问题,最终指向了创造性地解决上述问题的“市场设计”领域,令人叹为观止。
这套理论极具实用价值,不仅挽救了很多肾衰竭患者的生命,还改善了城市管理者颇为头疼的升学择校制度,甚至为美国政府带来了高达780亿美元的拍照拍卖收益。
如果觉得本文介绍的不过瘾,想要进一步了解此书的,建议深入阅读。一顿饭钱就可以买到别人可能一辈子的心血,这买卖,值!
后记:
理论归理论,爱情是最不需要理论的东西。它开始的原因可能仅仅是在人群中多看了你一眼,两个人之间因荷尔蒙产生的相互吸引,或因外貌,或因才华。在现实生活中,我们不可能同时与几位异性保持交往,并对他们的脾气秉性了如指掌,并且知晓他们的喜好,能够权衡利弊从中择优。但是匹配理论也给我们一些思考,让我们知道怎样的婚姻才是最稳定的。
我最后想说的是,遇到喜欢的人要珍惜,两情相悦才是最重要的。生活琐碎,没有习惯不了的习惯,也没有非得争论输赢的事情,珍惜眼前人。如果因小事而放弃继而寻找更加的合适,你永远也找不到那个更合适的。
快乐是选择,重要的是你对待人或事的态度,而不是人或事本身。