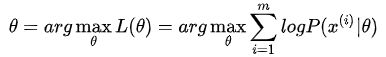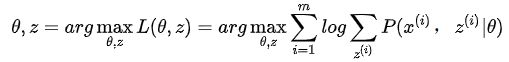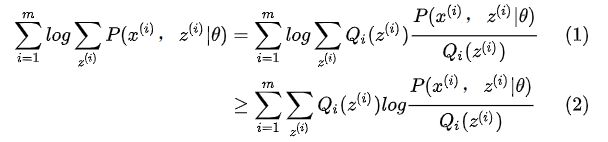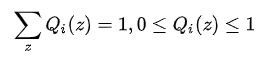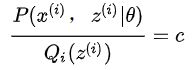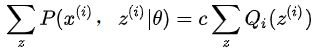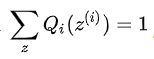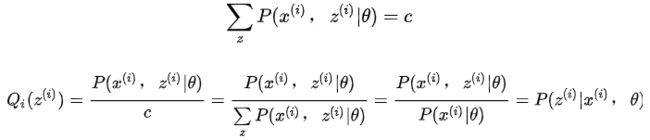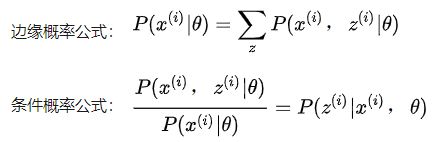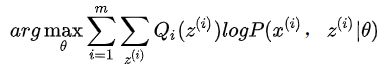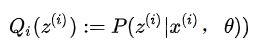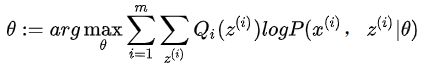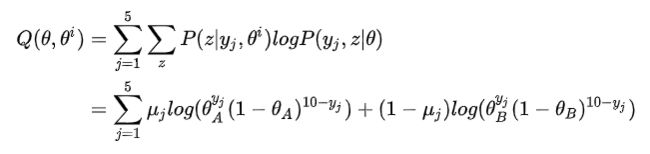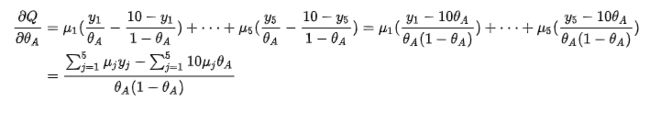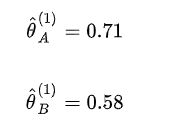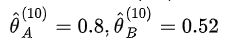EM(Expectation Maximization)算法是一种迭代算法,用于含有隐变量的概率模型参数的极大似然估计,或极大后验估计。EM算法的每次迭代由两步组成:E步,求期望(expectation);M步,求极大值,因而被称为期望极大算法,简称EM算法。
本文从EM算法的引入说起,简单介绍EM算法的推导过程,以及其在高斯混合模型中的应用。更多的关于EM算法的推导细节,可参见人人都懂EM算法。
引子
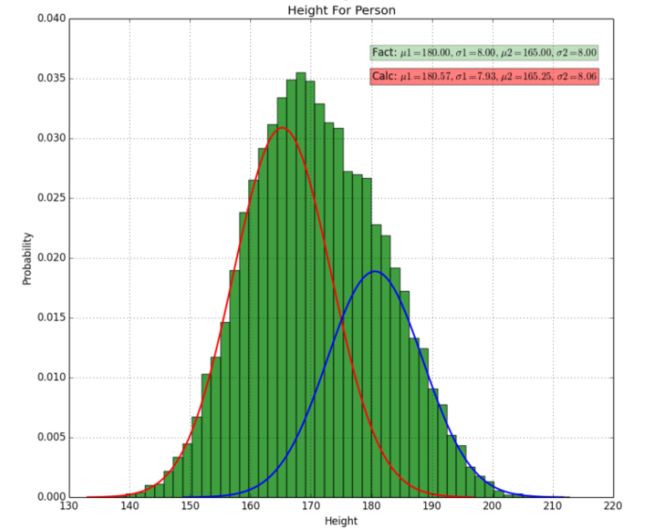
假设我们需要调查我们学校学生的身高分布。我们先假设学校所有学生的身高服从正态分布 。(注意:极大似然估计的前提一定是要假设数据总体的分布,如果不知道数据分布,是无法使用极大似然估计的),这个分布的均值μ和标准差为σ 未知,如果我们估计出这两个参数,那我们就得到了最终的结果。那么怎样估计这两个参数呢?
学校的学生这么多,我们不可能挨个统计吧?这时候我们需要用到概率统计的思想,也就是抽样,根据样本估算总体。假设我们随机抽到了 200 个人(也就是 200 个身高的样本数据,为了方便表示,下面“人”的意思就是对应的身高)。然后统计抽样这 200 个人的身高。根据这 200 个人的身高估计均值 μ和方差σ 。例子来自人人都懂EM算法。
现在我们假设这200个人的身高服从一个正态分布N(μ,σ),因此可以直接使用极大似然估计方法估计出这个分布的参数μ和σ。
但是,这200个人的身高真的是服从同一个正态分布吗?实际情况并不是这样的,男生和女生分别服从两种不同的正态分布,即男生 女生各服从一个正态分布 ,(注意:EM算法和极大似然估计的前提是一样的,都要假设数据总体的分布,如果不知道数据分布,是无法使用EM算法的),而且假设我们现在只有身高数据,丢失了性别数据,那么该怎样评估学生的身高分布呢?
这个时候,对于每一个样本或者你抽取到的人,就有两个问题需要估计了,一是这个人是男的还是女的,二是男生和女生对应的身高的正态分布的参数是多少。这两个问题是相互依赖的:
- 当我们知道了每个人是男生还是女生,我们可以很容易利用极大似然对男女各自的身高的分布进行估计。
- 反过来,当我们知道了男女身高的分布参数我们才能知道每一个人更有可能是男生还是女生。例如我们已知男生的身高分布为 N1(μ1=172,σ^2 =25),女生身高分布为N2(μ=162,σ^2=25)。此时如果有一个学生的身高为180,我们可以推断出这个学生为男生的可能性更大。
但是现在我们既不知道每个学生是男生还是女生,也不知道男生和女生的身高分布。这就成了一个先有鸡还是先有蛋的问题了。鸡说,没有我,谁把你生出来的啊。蛋不服,说,没有我,你从哪蹦出来啊。为了解决这个你依赖我,我依赖你的循环依赖问题,总得有一方要先打破僵局,不管了,我先随便整一个值出来,看你怎么变,然后我再根据你的变化调整我的变化,然后如此迭代着不断互相推导,最终就会收敛到一个解(草原上的狼和羊,相生相克)。这就是EM算法的基本思想了。
EM算法的引入
EM的意思是“Expectation Maximization”,具体方法为:
- 先设定男生和女生的身高分布参数(初始值),例如男生的身高分布为 N1(μ1=172,σ^2 =25), 女生的身高分布为N2(μ=162,σ^2=25)。当然了,刚开始肯定没那么准;
- 然后计算出每个人更可能属于第一个还是第二个正态分布中的(例如,这个人的身高是180,那很明显,他极大可能属于男生),这个是属于Expectation 一步;
- 现在,我们已经大概地按上面的方法将这 200 个人分为男生和女生两部分,我们就可以根据之前说的极大似然估计分别对男生和女生的身高分布参数进行估计(这不变成了极大似然估计了吗?极大即为Maximization)这步称为 Maximization;
- 然后,当我们更新这两个分布的时候,每一个学生属于女生还是男生的概率又变了,那么我们就再需要调整E步;
- ……如此往复,直到参数基本不再发生变化或满足结束条件为止。
上面的学生属于男生还是女生我们称之为隐含参数,女生和男生的身高分布参数称为模型参数。
EM 算法解决这个的思路是使用启发式的迭代方法,既然我们无法直接求出模型分布参数,那么我们可以先猜想隐含参数(EM 算法的 E 步),接着基于观察数据和猜测的隐含参数一起来极大化对数似然,求解我们的模型参数(EM算法的M步)。由于我们之前的隐含参数是猜测的,所以此时得到的模型参数一般还不是我们想要的结果。我们基于当前得到的模型参数,继续猜测隐含参数(EM算法的 E 步),然后继续极大化对数似然,求解我们的模型参数(EM算法的M步)。以此类推,不断的迭代下去,直到模型分布参数基本无变化,算法收敛,找到合适的模型参数。
EM算法的推导
Jensen不等式
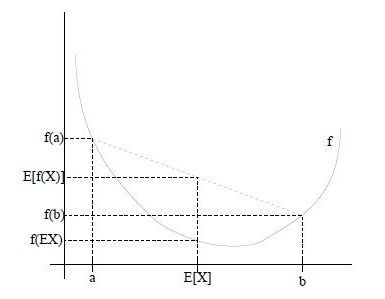
在开始介绍EM算法之前,让我们先来了解一个重要的定理——Jensen不等式。
如下图,如果函数f(x)是凸函数,x是随机变量,有 0.5 的概率是 a,有 0.5 的概率是 b, x的期望值就是 a 和 b 的中值了,那么:
特别地,如果函数f(x)是严格凸函数,当且仅当p(x=E(x))=1(即随机变量是常量)时等号成立。EM算法推导
对于m个相互独立的样本:
此时的(x, z)即为完全数据,样本的模型参数为θ,则观察数据x (i)的概率为P(x (i)|θ),完全数据(x (i), z (i))的似然函数为P(x (i), z (i)|θ)。
假如没有隐含变量z, 我们仅需要找到合适的θ极大化对数似然函数即可:
增加隐含变量z之后,我们的目标函数变成了找到合适的θ和z让对数似然函数极大: 多了一个变量,我们分别对这两个变量分别求偏导可以吗?理论上是可行啊,然而如果分别对未知的θ和z分别求偏导,由于logP(x (i)|θ)是P(x (i), z (i)|θ)的边缘概率,转化为logP(x (i)|θ)求导后形式会非常复杂(log(f 1(x)+f 2(x)+...复合函数的求导),所以很难求解得到θ和z,那么我们想一下可不可以将加号从log中提取出来呢?我们可以利用Jensen不等式对这个式子进行缩放如下: 上式(1)中引入了一个未知的新的分布Q i(z (i)),比照前面身高的例子,这里的Q分布中的不同z就相当于男女生的不同的分布,Q i(z (i))满足: 第二个式子用到了Jensen不等式(对数函数是凹函数): 其中:现在我们给定一个θ值(初始化θ),那么logL(θ)的值就取决于Qi(z)和P(x(i),z(i))。我们可以通过调整这两个概率使下届逼近logL(θ)的真实值,当不等式变为等式时,说明我们调整后的下届就等于logL(θ)了。由Jeson不等式可知,等式成立的条件是随机变量是常数,则有:
其中c为常数,对于任意i,有: 方程两边同时累加和: 又由于等式右边Q i(z i)概率求和等于1: 因此有:其中: 从上面可以看出Q(z)是已知样本和模型参数下的隐变量分布。
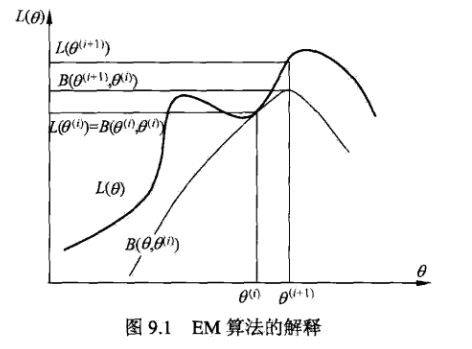
如果Qi(z(i)) = P(z(i)|x(i), θ),则(2)式使我们包含隐藏数据的对数似然函数的一个下届。如果我们能极大化这个下届,则也在尝试极大化我们的对数似然函数。即我们需要极大化下式:
到这里,我们就推出了在固定参数θ后Q i(z (i)) 的选择问题,从而建立了logL(θ)的下届,这是E步,接下来的M步就是在固定了Q i(z (i)) 后,求最佳的θ,去极大化logL(θ)的下届。
由于对logaf(x)求导的结果与f(x)的系数无关((ln(ax))'= (lna + lnx)'=1/x),因此对θ求极大似然时,可以去掉式中的常数部分Qi(z(i)):
EM算法流程
现在,让我们来总结一下EM算法的流程。
输入:观察数据x = (x(1), x(2), ... , x(m)), 联合分布P(x, z|θ),条件分布P(z|x,θ),极大迭代次数J。
(1)随机初始化模型参数θ值;
(2)迭代求解各个分布模型的参数以及各个模型的概率:
for j from 1 to J:
- E步:计算联合分布的条件概率期望:
- M:极大化L(θ),得到θ:
- 重复E、M步骤直到θ收敛
输出:模型参数θ
EM算法的另一种理解
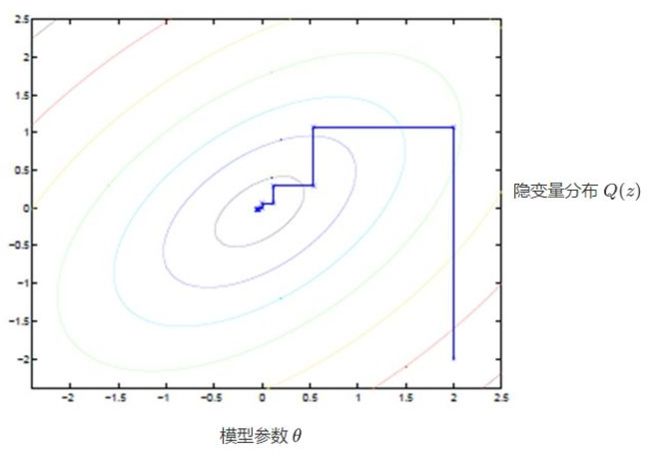
坐标上升法(Coordinate ascent)(类似于梯度下降法,梯度下降法的目的是最小化代价函数,坐标上升法的目的是最大化似然函数;梯度下降每一个循环仅仅更新模型参数就可以了,EM算法每一个循环既需要更新隐含参数和也需要更新模型参数。图中的直线式迭代优化的路径,可以看到每一步都会向最优值前进一步,而且前进路线是平行于坐标轴的,因为每一步只优化一个变量。
这犹如在x-y坐标系中找一个曲线的极值,然而曲线函数不能直接求导,因此什么梯度下降方法就不适用了。但固定一个变量后,另外一个可以通过求导得到,因此可以使用坐标上升法,一次固定一个变量,对另外的求极值,最后逐步逼近极值。对应到EM上,E步:固定 θ,优化Q;M步:固定 Q,优化 θ;交替将极值推向极大。
一个栗子
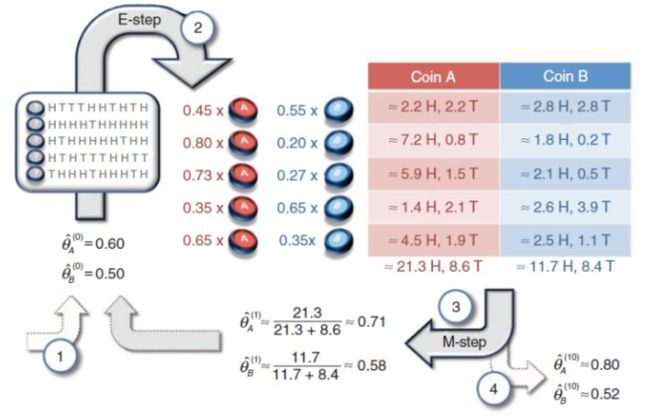
假设有两枚硬币A、B,随机选择一个硬币,进行十次掷硬币,共进行了五次实验(也即掷了50次),结果为H、T、T、T、H、H、T、H、T、H (H代表正面朝上),现在使用EM算法来求两个硬币正面出现的概率。E步:初始化θA=0.6和θB=0.5(θA和θB分别表示两个硬币出现正面的概率),计算每次掷硬币选择A和B的概率,例如第一个实验中选择A的概率为:
计算出每个实验为硬币 A 和硬币 B 的概率,然后进行加权求和。M步:求出似然函数下届Q(θ,θi), yi代表第j次试验正面朝上的个数,μj代表第j次试验选择硬币A的概率,1-μj代表第j次试验选择硬币B的概率。
针对Q函数求导,例如对θ A求导:求导为0之后就可以得到图中第一次迭代之后的参数值:
第二轮迭代:基于第一轮EM计算好的θ Aθ B,进行第二轮EM迭代,计算每个实验中选择的硬币是A和B的概率(E步),然后再计算M步,如此继续迭代... ...迭代十步之后,可以得到如下结果:
参考:
人人都懂EM算法
《统计学习方法》. 李航