1.语言模型
假设序列\(w_1, w_2, \ldots, w_T\)中的每个词是依次生成的,我们有
\[ \begin{align*} P(w_1, w_2, \ldots, w_T) &= \prod_{t=1}^T P(w_t \mid w_1, \ldots, w_{t-1})\\ &= P(w_1)P(w_2 \mid w_1) \cdots P(w_T \mid w_1w_2\cdots w_{T-1}) \end{align*} \]
例如,一段含有4个词的文本序列的概率
\[ P(w_1, w_2, w_3, w_4) = P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_1, w_2, w_3). \]
语言模型的参数就是词的概率以及给定前几个词情况下的条件概率。设训练数据集为一个大型文本语料库,如维基百科的所有条目,词的概率可以通过该词在训练数据集中的相对词频来计算,例如,\(w_1\)的概率可以计算为:
\[ \hat P(w_1) = \frac{n(w_1)}{n} \]
其中\(n(w_1)\)为语料库中以\(w_1\)作为第一个词的文本的数量,\(n\)为语料库中文本的总数量。
类似的,给定\(w_1\)情况下,\(w_2\)的条件概率可以计算为:
\[ \hat P(w_2 \mid w_1) = \frac{n(w_1, w_2)}{n(w_1)} \]
其中\(n(w_1, w_2)\)为语料库中以\(w_1\)作为第一个词,\(w_2\)作为第二个词的文本的数量。
2.n-gram
序列长度增加,计算和存储多个词共同出现的概率的复杂度会呈指数级增加。\(n\)元语法通过马尔可夫假设简化模型,马尔科夫假设是指一个词的出现只与前面\(n\)个词相关,即\(n\)阶马尔可夫链(Markov chain of order \(n\)),如果\(n=1\),那么有\(P(w_3 \mid w_1, w_2) = P(w_3 \mid w_2)\)。基于\(n-1\)阶马尔可夫链,我们可以将语言模型改写为
\[ P(w_1, w_2, \ldots, w_T) = \prod_{t=1}^T P(w_t \mid w_{t-(n-1)}, \ldots, w_{t-1}) . \]
以上也叫\(n\)元语法(\(n\)-grams),它是基于\(n - 1\)阶马尔可夫链的概率语言模型。例如,当\(n=2\)时,含有4个词的文本序列的概率就可以改写为:
\[ \begin{align*} P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_1, w_2, w_3)\\ &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_2) P(w_4 \mid w_3) \end{align*} \]
当\(n\)分别为1、2和3时,我们将其分别称作一元语法(unigram)、二元语法(bigram)和三元语法(trigram)。例如,长度为4的序列\(w_1, w_2, w_3, w_4\)在一元语法、二元语法和三元语法中的概率分别为
\[ \begin{aligned} P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2) P(w_3) P(w_4) ,\\ P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_2) P(w_4 \mid w_3) ,\\ P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_2, w_3) . \end{aligned} \]
当\(n\)较小时,\(n\)元语法往往并不准确。例如,在一元语法中,由三个词组成的句子“你走先”和“你先走”的概率是一样的。然而,当\(n\)较大时,\(n\)元语法需要计算并存储大量的词频和多词相邻频率。
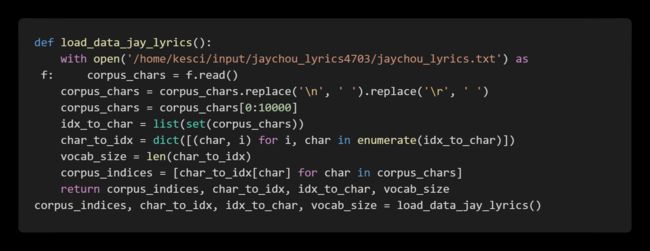
3.数据集
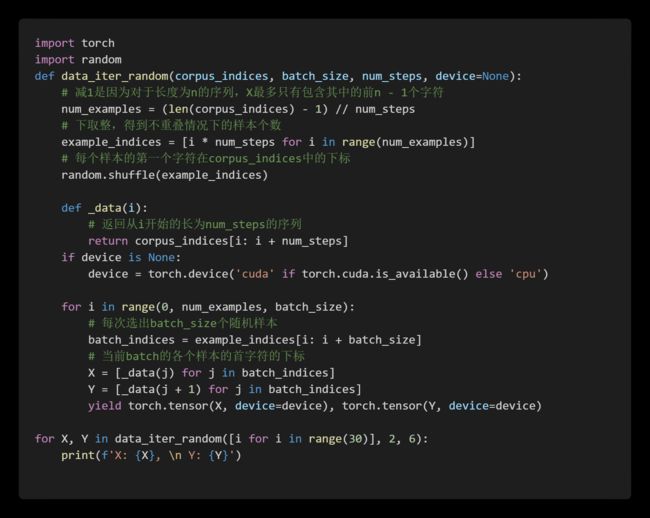
4.时序数据采样
4.1 随机采样
相邻的两个随机小批量在原始序列上的位置不一定相毗邻。
X: tensor([[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]]),
Y: tensor([[13, 14, 15, 16, 17, 18],
[19, 20, 21, 22, 23, 24]])
X: tensor([[ 6, 7, 8, 9, 10, 11],
[ 0, 1, 2, 3, 4, 5]]),
Y: tensor([[ 7, 8, 9, 10, 11, 12],
[ 1, 2, 3, 4, 5, 6]])4.2相邻采样
在相邻采样中,相邻的两个随机小批量在原始序列上的位置相毗邻。
X: tensor([[ 0, 1, 2, 3, 4, 5],
[15, 16, 17, 18, 19, 20]]),
Y: tensor([[ 1, 2, 3, 4, 5, 6],
[16, 17, 18, 19, 20, 21]])
X: tensor([[ 6, 7, 8, 9, 10, 11],
[21, 22, 23, 24, 25, 26]]),
Y: tensor([[ 7, 8, 9, 10, 11, 12],
[22, 23, 24, 25, 26, 27]])