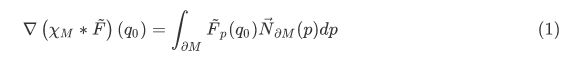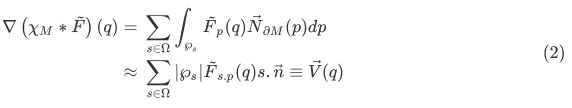从点云到网格（三）Poisson重建

Possion重建是Kazhdan等2006年提出的网格重建方法[1]。Possion重建的输入是点云及其法向量，输出是三维网格。Poisson有公开的源代码[2]。PCL中也有Poisson的实现。

核心思想

Possion重建是一个非常直观的方法。它的核心思想是点云代表了物体表面的位置，其法向量代表了内外的方向。通过隐式地拟合一个由物体派生的指示函数，可以给出一个平滑的物体表面的估计。

给定一个区域\(M\)及其边界\(\partial M\)，指示函数\(\chi_M\)定义为

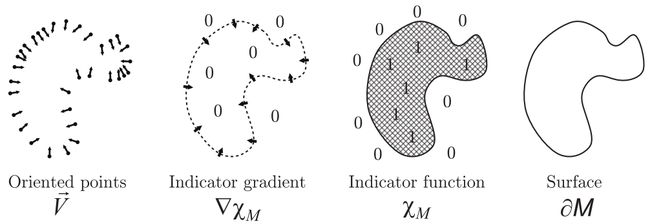
这样，把重构\(S = \partial M\)的问题转换为重构\(\chi_M\)的问题。作者给出了将点云及其法向量和\(\chi_M\)联系起来的公式。作者论文中的图1非常形象地描述了这二者的联系。

基本思路

对于任意点\(p\in \partial M\)，定义\(\vec{N}_{\partial M}(p)\)为向内的表面法向量，\(\tilde{F}(q)\)为一个平滑滤波器，\(\tilde{F}_p(q)=\tilde{F}(q-p)\)为\(\tilde{F}\)沿\(p\)方向的平移。因为\(\chi_M\)一般意义上是不好求导的，这里用\(\chi_M\ast\tilde{F}\)的导数来近似。

从法向量到梯度空间

梯度空间的近似

由于\(\vec{N}_{\partial M}\)的分布是未知的，需要通过观测值\(P=\left\lbrace \left( p_i,n_i\right) \right\rbrace\)来近似。考虑离散点集\(\Omega\)，\(\partial M\)被分割为互不相交的区域\(\wp_s,s\in\Omega\)。\((1)\)可以转化为积分求和，并将每个小积分近似为常函数，用代表点\(s.p\)对应的函数值和\(\wp_s\)的面积的乘积代替。

这里希望平滑滤波器\(\tilde{F}\)能够尽量地窄，不过分平滑数据，同时尽量地宽，使得积分近似能够更准确。高斯滤波器是一种常见的选择。

求解Possion问题

向量空间\(\vec{V}\)和指示函数\(\tilde{\chi}\)满足
\[ \nabla\tilde{\chi}=\vec{V} \tag{3} \]
然而，\(\vec{V}\)通常意义上是没法积分的（为什么？）。为了得到\((3)\)式的最小二乘解，将\((3)\)式两边求导，就得到了拉普拉斯方程
\[ \Delta\tilde{\chi}=\nabla\cdot\vec{V} \tag{4} \]

拉普拉斯方程在数学上有很详细的研究。

实现细节

空间划分

为了解一个偏微分方程问题，首先要将其离散化。最简单的方法是将空间划分为均匀网格。这种划分非常占内存空间，而且只有边界附近的值才是我们关心的，大量的空间被浪费了。作者采用了一种自适应的网格结构octree来划分空间，并且octree上定义了一个函数空间\(F_o\)。下图给出了octree在三维空间对一个物体的划分。物体边缘的网格密度远大于远离物体的网格密度。

http://http.developer.nvidia.com/GPUGems2/elementLinks/37_octree_03.jpg

空间上的基函数选择

如何选择函数空间\(F_o\)实际上挺有学问的。因为\(F_o\)一旦给定，定义在这个octree上的向量空间\(\vec{V}\)和指示函数\(\chi\)都会通过\(F_o\)的线性组合去近似。这样，求解\(\chi\)就转化为求解\(F_o\)上的参数组合，进而转化为求解一个线性方程组。

给定octree的深度\(D\)，作者根据选择了下面的基函数\(F\)。

\(*n\)代表\(n\)次卷积。当\(n\)趋向于无穷时，\(F\)趋向于高斯函数，它的定义域也越来越大。当\(n=3\)时，定义域为\([-1.5,1.5]^3\)。

octree上某个节点\(o\)对应的函数\(F_o\)定义为
\[ F_o(q)\equiv F\left(\frac{q-o.c}{o.w}\right)\frac{1}{(o.w)^3} \]
其中\(o.c\)是的\(o\)中心，\(o.w\)是\(o\)的宽度。假设根节点（第0层）的宽度为\(W\)，那么第\(d\)层节点的宽度为\(\frac{W}{2^{d}}\)。这个函数空间和小波空间很像。

Possion求解

Possion求解方法是L2投影（L2 projection）[3]。定义octree的节点集合为\(O\)。向量空间\(\vec{V}\)可以近似为
\[ \vec{V}(q)\equiv \Sigma_{s\in \Omega}\Sigma_{o\in Ng(s)}\alpha_{o,s}F_o(q)s.\vec{n} \]
其中\(Ng(s)\)是\(s\)的八个最近邻的叶节点，\(\alpha_{o,s}\)是三线性插值的权重。

虽然\(\vec{V}\)和\(\tilde{\chi}\)都可以在函数空间上表示出来，\(\Delta\tilde{\chi}\)和\(\nabla\cdot\vec{V}\)却未必有定义。因此将\((4)\)近似为最小化其在\(F_o\)上的投影
\[ \Sigma_{o} \lVert\langle \Delta \tilde{\chi}-\nabla\cdot\vec{V},F_o\rangle\lVert^2=\Sigma_{o} \lVert\langle \Delta \tilde{\chi},F_o\rangle-\langle\nabla\cdot\vec{V},F_o\rangle\lVert^2 \]
令\(\tilde{\chi}=\Sigma_ox_oF_o\)，那么求解\(\tilde{\chi}\)即是求解\(x_o\)。
\[ \langle \Delta \tilde{\chi},F_{o'}\rangle=\Sigma_{o}x_{o}\langle \Delta F_o,F_{o'}\rangle \]
\[ \Sigma_{o} \lVert\langle \Delta \tilde{\chi},F_o\rangle-\langle\nabla\cdot\vec{V},F_o\rangle\lVert^2 =\Sigma_{o'}\lVert\Sigma_ox_o\langle \Delta F_o,F_{o'}\rangle-\langle\nabla\cdot\vec{V},F_{o'}\rangle\lVert^2 \]
上式右边对\(x=\lbrace x_o\rbrace\)求偏导，转化为
\[ \min \limits_{x}\left\lVert Lx-v \right\lVert ^2 \]
其中，设octree的节点数为\(N\)，\(N\times N\)矩阵\(L\)在\((o,o')\)位置上的值为
\[ L_{o,o'}\equiv \langle\frac{\partial^2 F_o}{\partial x^2},F_{o'}\rangle+\langle\frac{\partial^2 F_o}{\partial y^2},F_{o'}\rangle+\langle\frac{\partial^2 F_o}{\partial z^2},F_{o'}\rangle \]

表面提取

用Marching Cubes类似的方法。注意iso的值取自\(S\)个划分的平均。

作者还讨论了非均匀采样下的算法，在此就不赘述。

Poisson分析

简单列几点

• Poisson在边缘处的锐度比VRIP要好。这是因为VRIP在大的边缘处TSDF的累加会有平滑效应，而Poisson依据的是法向量，不会引入额外的平滑。
• VRIP是局部方法，每次只更新当前深度图对应的TSDF。Poisson是全局方法。
• 从个人使用经验上看，Poisson对于噪声更加鲁棒一些。点云法向量估计的精度不能太差。
• 如果重建出奇怪的形状（分层、分块），请查看原始点云是否平滑，是否有噪声，调整生成网格的分辨率以适应点云。

小结

Poisson是个好方法。

参考文献

[1]. Kazhdan, Michael, Matthew Bolitho, and Hugues Hoppe. "Poisson surface reconstruction." Proceedings of the fourth Eurographics symposium on Geometry processing. Vol. 7. 2006.
[2]. http://www.cs.jhu.edu/~misha/Code/PoissonRecon/Version8.0/
[3]. http://www.featflow.de/en/software/featflow2/tutorial/tutorial_l2proj.html