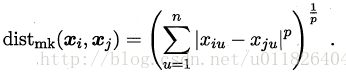本章参考周志华《机器学习》第九章编写
首先介绍了聚类问题中的性能度量和距离计算,之后介绍了具体的聚类算法。有基于原型的三种聚类算法:k-Means/LVQ/混合高斯。密度聚类。层次聚类。其中除了混合高斯聚类的推导比较复杂之外,其他聚类算法的思想都很直接,很好理解。
9.1 聚类任务
首先我们先来认识一下什么是聚类任务。
聚类是“无监督学习(unsupervised learning)”中重要的一种。其目标是:通过对无标记的训练样本学习,来揭示数据内在的性质以及规律,为进一步的数据分析做基础。聚类的结果是一个个的簇(Cluster)。所以来说,聚类通常作为其他学习算法的先导,比如在分类问题中,常常先做聚类,基于聚类的不同簇来进行分类模型的训练。
我们先来认识一下聚类算法涉及到两个基本问题:性能度量 & 距离计算。后面我们再具体讲解聚类的经典算法。
9.2 性能度量
由于聚类算法是无监督式学习,不依赖于样本的真实标记。所以聚类并不能像监督学习例如分类那样,通过计算对错(精确度/错误率)来评价学习器的好坏或者作为学习器的优化目标。一般来说,聚类有两类性能度量指标:外部指标和内部指标
9.2.1 外部指标
所谓外部,是将聚类结果与某个参考模型的结果进行比较,以参考模型的输出作为标准,来评价聚类的好坏。假设聚类给出的结果为 λ,参考模型给出的结果是λ*,则我们将样本进行两两配对,定义:
上面的这些参数,可以直观的理解为聚类结果和标准结果的差别。在这些参数的基础上,给出如下的指数作为聚类的外部指标:
9.2.2 内部指标
内部指标不依赖任何外部模型,直接对聚类的结果进行评估。直观来说:簇内高内聚,簇间低耦合。定义:
基于上面的4个距离,定义出如下的内部指标:
至此为止,我们定义除了外部指标和内部指标,可以用作聚类算法的优化目标,使得聚类算法更加准确。
下面看,关于距离的定义。
9.3 距离度量
我们从小学的距离都是欧氏距离。这里介绍几种其他的距离度量方法:
-
“闵可夫斯基距离(Minkovski Distance)”:
-
“曼哈顿距离(Manhattan Distance)”:当上面的 p=1 时候,就是曼哈顿距离。所谓的曼哈顿距离,就是说在坐标轴上的距离而不是直接的两点之间的直线距离(欧氏距离)。
-
欧氏距离(Euclidean Distance):p=2
之前提到过,属性值分为连续属性和离散属性,对于连续属性,一般都可以直接被学习器使用,而离散属性我们根据是否存在序关系(大小关系)来做归一化等处理。之前提到过这样的处理方式。
若属性值之间存在序关系,则可以将其转化为连续值,例如:身高属性“高”“中等”“矮”,可转化为{1, 0.5, 0}。 若属性值之间不存在序关系,则通常将其转化为向量的形式,例如:性别属性“男”“女”,可转化为{(1,0),(0,1)}。
这里对于无需属性我们用闵可夫斯基距离就不能做,需要用VDM距离进行计算,对于离散属性的两个取值a和b,定义:
所以在计算两个样本的距离时候,将两种距离混合在一起进行计算:
最后需要注意的是:这里我们通过列举的方法给出了不同的距离计算方式。但实际上根据实际问题的不同,还需要根据样本来给出不同的距离极计算公式,不仅限于我们给出的几种。
9.4 原型聚类
原型聚类即“基于原型的聚类(prototype-based clustering)”,原型指的是样本空间中具有代表性的点(类似于K-Means 选取的中心点)。通常情况下来说,算法现对原型进行初始化,然后对原型进行迭代更新求解。而不同的初始化形式和不同的求解方法,最终会得到不同的算法。常见的 K-Means 便是基于簇中心来实现聚类;混合高斯聚类则是基于簇分布来实现聚类。下面我们具体看一下几种算聚类算法:
9.4.1 K-Means
K-Means 聚类的思想十分简单,首先随机指定类中心,根据样本与类中心的远近划分类簇;然后重新计算类中心,迭代直至收敛。实际上,迭代的过程是通过计算得到的。其根本的优化目标是平方误差函数E:
其中 u_i 是簇 C_i 的均值向量。直观上来看,上式刻画了簇内样本围绕簇均值向量(可以理解为簇中心)的紧密程度,E值越小,则簇内样本的相似度越高。
具体的算法流程如下:
书上还给出了基于具体西瓜样本集的计算过程说明。可以看一下。
9.4.2 学习向量量化(Learning Vector Quantization)
LVQ 也是基于原型的聚类算法,与K-Means 不同的是, LVQ使用样本的真实类标记来辅助聚类。首先,LVQ根据样本的类标记,从各类中分别随机选出一个样本作为该类簇的原型,从而形成了一个原型特征向量组,接着从样本集中随机挑选一个样本,计算其与原型向量组中每个向量的距离,并选取距离最小的向量所在的类簇作为该样本的划分结果,再与真实类标比较:
- 若划分结果正确,则对应原型向量向这个样本靠近一些
-
若不正确,远离一些。
可以看到,最后输出的是一组原型向量。可以理解为一组中心点。
9.4.3 高斯混合聚类
可以看到,K-Means 和 LVQ 都是以类中心作为原型指导聚类,而高斯混合聚类则采用高斯分布来描述原型。现在假设每个类簇中的样本都服从一个多维高斯分布,那么空间中的样本可以看做由K个多维高斯分布混合而成。
多维高斯的概密为:
其中 \miu 表示均指向量,\sum 表示协方差矩阵,可以看出一个多为高斯由这两个参数确定。下面我们给出混合多维高斯概密:
其中,α称为混合系数,这样空间中样本的采集过程则可以抽象为: (1)先选择一个类簇(高斯分布)(2)再根据对应高斯分布的密度函数进行采样,
这时候,后验概率代表选出的样本 x_j 由 第i个高斯混合成分生成。
将后验概率用 Bayes 公式展开:
当整个高斯混合分布已知时,高斯混合聚类的划分方法是: 将样本集D按照,每个样本选择后验概率最大的簇划分进行聚类
从原型聚类的角度来看, 高斯混合聚类是采用概率模型(高斯模型)刻画原型,而具体的簇划分则是由原型对应的后验概率确定。
即:每个样本x_j 的簇标记 \lambda_j 按照下式确定(其中 \gamma 代表上面的后验概率):
所以这个时候我们需要计算后验概率,那自然就需要知道模型参数 (\alpha, \mu, \sum)。这里对于给定给的混合模型,给定的数据集D,自然用 ML 来构建目标函数,即最大化似然:
直接求偏导为0是计算不出的,这里要用EM算法来做:E步,对高斯分布参数和混合系数随机初始化,通过下面推导出的参数公式,计算各个后验概率 \gamma;M步,最大化似然函数(即LL(D)分别对三个参数求偏导为0);迭代,收敛
具体的算法流程如下:
9.5 密度聚类
密度聚类是基于密度的聚类,它从个样本分布的角度来考察样本之间的可连接性,并基于可连接性(密度可达)不断拓展疆域(类簇)。最著名的就是DBSCAN(Density-Based Spatial Clustering of Applications with Noise),首先我们需要明白以下概念:
直观来理解DBSCAN就是:找出一个核心对象所有密度可达的样本集合形成簇。
首先,从样本集中随便选出一个核心样本A,找出所有A密度可达的样本集合,将这些样本形成一个密度相连的类簇;直到所有的核心对象都遍历完成。当然,可能会出现一些不输入任何簇的样本,这样的样本我们称为 noise 噪声样本。
其算法流程度如下所示:
可以看到,整个DBSCAN算法从直观上理解起来非常简单,而且跟之前的 k-Means 和 LVQ 模型在思想上有一定的相似之处。
9.6 层次聚类 (Hierarchical clustering)
层次聚类试图在不同层次对数据集进行划分,从而形成属性的聚类结构。
这里介绍一种“自底向上”结合策略的 AGNES(AGglomerative NESting)算法。假设有N个待聚类的样本,AGNES算法的基本步骤如下:
1. 初始化:把每个样本归为一类,计算每两个类之间的距离,也就是样本与样本之间的相似度;
2. 寻找各个类之间最近的两个类,把他们归为一类(总类数目就少了一个);
3. 重新计算新生成类和各个旧类之间的相似度;
4. 重复2和3,知道类别数目达到预设的类簇数目,结束
可以看出其中最关键的一步就是 计算两个类簇的相似度,这里有几种度量方法:
(1)单链接(singal-linkage):取类间最小距离
(2)全链接(Complete-linkage):取类间最大距离
(3)均链接(average-linkage):取类间两两平均距离
可以看出的是,单链接的包容性很强,全链接则是要求极高,只要存在缺电就坚决不合并,均链接则是从全局出发。
层次聚类算法流程图如下:
书上给出了在西瓜数据集上的例子,可以具体看一下。
可以发现,层次聚类的思想也是十分直观的。