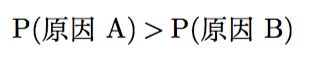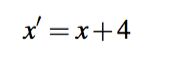奥卡姆剃刀
奥卡姆剃刀(Occam's Razor),是由14世纪逻辑学家、圣方济各会修士奥卡姆的威廉(William of Occam)提出的一个解决问题的法则。这个法则的表述很多,其中最流行的莫过于:
如非必需,勿增实体
(More things should not be used than are necessary)
换句话说,如果关于一个或多个现象,有许多种理论都能作出同样准确的解释,那么应该挑选其中使用假定最少的。
其实,除了这位奥卡姆之外,有很多名人,包括我们的老子,也都说过类似的话:
- 老子:大道至简;为学日益,为道日损。
- 亚里士多德: 自然界选择最短的道路。(Nature operates in the shortest way possible)
- 托勒密:我们认为一个很好的原则是通过最简单的假设来解释现象(We consider it a good principle to explain the phenomena by the simplest hypothesis possible)
- 伽利略:大自然不会无缘无故的增加事物;她善于利用最简单和最容易的手段来达到目的;她从来不做徒劳无功的事情(Nature does not multiply things unnecessarily; that she makes use of the easiest and simplest means for producing her effects)
- 牛顿:解释自然界的一切,应该追求使用最少的原理。如果很少的理由就能解释自然,那么再列举更多的理由就是多余的了(We are to admit no more causes of natural things than such as are both true and sufficient to explain their appearances. Nature does nothing in vain, and more is in vain when less will serve.)
- 爱因斯坦:凡事尽可能简洁,但不能太过简单(Everything should be made as simple as possible, but no simpler)
关于如何用奥卡姆剃刀帮我们找到现象背后的真理,维基百科上有两个例子
例子1: 树吹倒了
在一个有风的夜晚,有两棵树连根倒下了,除此之外没有任何别的痕迹。这是我们观察到的现象。
可以解释这两棵树倒掉的两个可能的解释为(1)风把他们吹倒了 (2)有两颗陨石从天而降,每颗陨石撞到了一棵树,并且最后两颗相互相撞,除去了自己的痕迹。
尽管这两个解释都可以很好的解释观察到的现象,但是后者一看就需要更多的假设:首先需要两颗陨石掉下来,正好砸到两个树上,这本身就相当罕见。此外,还需要陨石相互撞上而抹去他们自己的痕迹,这个也很罕见。因此,尽管第二个假设也可以解释树倒了这个现象,由于这第二个解释需要更多的且相当罕见的假设,我们仍然应该坚定不移的选择第一个解释,这就是用奥卡姆剃刀得到的结果。
例子2: 医生诊断
奥卡姆的剃刀也经常用于医生诊断中。当一个症状可以有多种病症对应时,医生应该首先怀疑的是最普遍的病症。例如,如果发现一个小孩流鼻涕,那么医生应该首先怀疑这个小孩是否患有感冒,而不是某一种罕见的先天性疾病。医学院的学生经常被老师告诫,“当你听到马蹄声的时候,要想到马,而不是斑马(When you hear hoofbeats, think horses, not zebras)。
例子3: 谁把花盆砸了
假设你一天晚上到家,看到你摆在客厅里的一盆花被砸在地板上,除了这盆花之外,家里没有任何其他的变化。你脑子里立刻列出几个可能的原因(1)花盆被一个鬼魂撞倒了,(2)花盆被一个偷偷闯入你家里的人碰倒了,并且他没有拿任何东西。(3)花盆被你家养的猫弄砸了。
首先,这三个原因都可以很好的解释这个现象。在这个前提下,用奥卡姆剃刀就可以很好的帮我们找到真相。首先,花盆被鬼魂碰倒了这个原因,需要非常多的很强的假设。因为首先需要鬼魂存在。这个假设非常强,因为到现在为止没有证据证明有鬼魂存在。并且,这个鬼魂还跑到你家里,专门把你家里的花给碰倒了。第二个原因的假设也很多。首先,需要假设有一个人闯入你家里,并且该人就是专门为了把你的花盆给砸了(除了花盆之外,家里没有任何损失)。在此,这个闯入你家里的人,要么有你们家的门钥匙,要么知道如何开锁以不留下任何痕迹。
而相比于这两个原因,第三个原因需要的假设并不强,你家里本来就有一只猫,并且猫碰到花盆,也不是一个特别小的概率。因此用奥卡姆剃刀来判断的话,一定会保留第三个。
例子4: 地心说和日心说
给我留下最深印象的,就是这个地心说和日心说。吴军老师在他的《数学之美》的第19章《谈谈数学模型的重要性》中,提到了这个例子。数学家和天文学家的托勒密的地心说中,由于从地球上看,行星的运动轨迹是不规则的,因此托勒密用了40-60个小圆套大圆的方法,精确地计算出了所有行星运动的轨迹,如下图所示。托勒密模型的精度之高,让后来所有的科学家都惊叹不已。即使今天,我们在计算机的帮助下,也很难解出40个套在一起的圆的方程。
而后,波兰天文学家哥白尼发现,如果以太阳为中心来描述星体的运行,只需要8-10个圆,就能计算出一个行星的运动轨迹,他因此提出了日心说。然而,很遗憾的是,哥白尼的模型的误差比托勒密模型的误差要大不少。所以日心说要想让人心服口服地接受,就得更准确地描述行星运动。
完成这一使命的是约翰内斯·开普勒。开普勒很幸运地发现了行星围绕太阳运转的轨道实际上是椭圆形的,这样不需要用多个小圆套大圆,而只要用一个椭圆就能将星体运动规律描述清楚了。只是开普勒的知识水平不足以解释为什么行星的轨迹是椭圆形的。解释行星运动的轨道为什么是椭圆形这个光荣而艰巨的任务,最后由伟大的科学家牛顿用万有引力定律解释得清清楚楚。
总结一下,拿到的观测是太阳系的某个星体的轨迹,有三个模型可以较好的解释上述的观测
- 托勒密的以地球为中心,40-60个小圆套大圆
- 哥白尼的以太阳为中心,8-10个圆
- 开普勒的以太阳为中心,一个椭圆。
我们可以看出,上述的模型一个比一个简单,由于它们都可以较好的解释观测到的轨迹,因此当然应该选最后一个。
用贝叶斯定理来解释奥卡姆剃刀
我们来回顾一下贝叶斯定理。当我们观察到某一个现象,或者拿到某一个证据的时候,我们总想找到现象背后的原因。与很多人的思考方式不同,贝叶斯并不是只选择一个,而是对所有的可能的原因,都找到一个概率,这个概率就是在观察到这个现象后,每个原因的概率。这个概率P(原因i|当前的观测),通常
被称为后验概率(Posterior probability)。后验概率中的`后',就是拿到观测/证据以后,再判断该原因的概率的含义。
贝叶斯定理给出了后验概率的表达式:
P(原因i)这个概率是我们在拿到现象/观测之前,我们对于原因i本身成立的概率的评估。这个通常称为先验概率(Prior probability)。先验概率中的`先',就是拿到观测之前的意思。先验概率依赖于原因i发生的概率,也就是这个原因是否常见。
P(当前的观测|原因i)是在原因i成立时,我们能够观察到该现象出现的概率,通常我们把这个叫做似然概率(Likelihood probability)。这个似然概率描述了原因i能够用来解释当前拿到的现象或观测的程度(解释力度)。解释的越好,那么似然概率就越大。
最后一个,P(当前的观测)这个概率描述了该观测到的现象发生的概率。注意不同的原因i对应的该概率都一样。这意味着,贝叶斯定理最后选择哪个原因,只取决于
P(原因 i)*P(当前的观测|原因 i)
这说明,贝叶斯定理选出的原因,是似然概率P(现象|原因)和先验概率P(原因)的乘积最大的。前者表示了该原因解释当前的现象的力度(解释的好不好),而后者表示了该原因发生的概率(常不常见)。通俗的来说,在一定程度上解释该现象(似然概率较高),并且本身也常见(先验概率较大)的原因最容易胜出。
现在我们用贝叶斯定理来解释奥卡姆剃刀。 首先,奥卡姆剃刀`如非必需,勿增实体'可以表示为,如果两个原因,原因A和原因B都可以很好的解释观测,并且原因A比原因B更简单的话,那么应该选择原因A。
`原因A和原因B都可以很好的解释观测'这句话用贝叶斯定理来解释,就是这两个原因的似然概率都比较大,即
`原因A比原因B更简单'这句话用贝叶斯定理来解释,就是原因A的先验概率比原因B要大,即
在这种情况下,奥卡姆剃刀选择了第一个原因。这个完全符合贝叶斯定理,因为贝叶斯定理选出的原因,就是先验概率和似然概率乘积最大的原因。
有人会问,为什么奥卡姆剃刀中的简单的原因,其先验概率比较大?因为简单的原因不需要那么多强假设就可以成立;而如果一个原因需要的假设越多,假设越强,那么它发生的概率就越低。例如,如果原因A需要2个假设成立才成立,每个假设自身的概率为10%,那么原因A的先验概率为
P(原因A)=1%,而如果原因B需要4个假设,每个假设成立的概率为10%,那么那么原因B的先验概率为P(原因B)=0.01%。
如果我们现在再看爱因斯坦说的那句话,
Everything should be made as simple as possible, but not simpler,
你就会认识到,as simple as possible,就是先验概率越大的原因越好;而 not simpler,就是说这个原因仍然需要能够解释当前的观测。这句话翻译成贝叶斯定理的语言,就是说,你最终找到的原因是在能够解释当前的观测的前提下,先验概率最大的那个原因。
所以我们可以说,奥卡姆剃刀,是贝叶斯定理的一种特殊情况。奥卡姆剃刀告诉我们,在多个有相同的解释力的原因中要选出一个简单的;而贝叶斯定理告诉我们更一般的情况,即在解释力和复杂性中找到最好的平衡。
在这种情况下,奥卡姆剃刀选择了第一个原因。这个完全符合贝叶斯定理,因为贝叶斯定理选出的原因,就是先验概率和似然概率乘积最大的原因。
所以我们可以说,奥卡姆剃刀,是贝叶斯定理的一种特殊情况。奥卡姆剃刀告诉我们,在多个有相同的解释力的原因中要选出一个简单的;而贝叶斯定理告诉我们更一般的情况,即在解释力和复杂性中找到最好的平衡。
我们再来看几个例子。
例子5: 树后面的箱子
这是一个被广泛用来解释奥卡姆剃刀的例子,原文出自MacKay D J C. Information theory, inference and learning algorithms[M]. Cambridge university press, 2003.。下图中有多少个箱子?特别地,那棵书后面是一个箱子?还是两个箱子?绝大多数人一眼看去,都会觉得树后面肯定是一个箱子而不是两个。我们来解释一下后面的道理。
首先我们来梳理一下这个问题中的观测和待定的原因。 首先,观测就是上面的图。 我们有两个备选原因需要考虑。
- h1:正好有一个箱子摆在如图所示的树的后面(见图\ref{fig:Occam_razor}下方的第一个小图)。
- h2: 正好有两个箱子摆在如图所示的树的后面(见图\ref{fig:Occam_razor}下方的第二个小图)。
我们来分析一下为什么选h1。
首先,h1和h2都可以完美的解释上面的图。其次,h1比h2要更简单,或者等价的,h1发生的可能性比h2要大。很容易看出,h2需要多个条件同时满足才能发生,包括(1)两个箱子的位置要正好在图中的位置,(2)两个箱子的高度要一致,(3)两个箱子的长度也要正好匹配,并且(4)两个箱子的颜色也要相同。 只要有一个条件不满足,那么就得不到上面的图了。简单的说就是,哪有这么巧的两个高度相同,长短合适、颜色相同的两个箱子正好摆在树后面?
相比于h2,h1所需要的假设就少得多,只需要一个箱子摆在图中的位置可以了。因此根据奥卡姆剃刀原理(或者贝叶斯定理),我们应选择h1,而不是h2。
例子6: 找规律填数字
很小的孩子,都会做下面的填下一个数字的题目。例如,给出下面这个序列的后两个数字:
-1,3,7,11
我想绝大部分人,都会立刻从前面4个数字看出一个规律:后面一个比前面一个增加4。 就是说,把前一个数字作为x,下一个数字x'满足
因此,11后面的两个数字应该为 15和19。
可是有没有想过,还有一个规律可以完全解释上面的4个数,即
用这么个模型来预测,那么后面的两个数就是-19.9和1043.8。
为什么这个模型能够同样完美的解释这4个数字,但是大家都不会采用它呢?主要原因在于,后面一个模型比前面一个模型要复杂的多。
同样两个模型,一个简单,一个复杂,都可以完美的解释这4个数,根据奥卡姆剃刀,选择前一个喽。
如果我们用贝叶斯定理来分析,就是这两个模型(原因),都可以完美的解释给出的4个数,但是第一个模型的先验概率要高于第二个模型,因此我们选择第一个模型。
我们来具体说明为什么简单的模型对应的先验概率比较高。 我们可以这么想,我们假设通过掷骰子来产生上面两个模型的所有的系数。为了能找到系数,我们假设掷的骰子是类似于下图中的多面骰子。我们这里的骰子有101面,每一个面上是一个整数,依次从-50到50。此外,每个系数,都从掷的两颗骰子A和B的数字的比值来决定。例如掷出的两颗骰子的数字为-10和1,那么就得到了一个系数-10。
模型1包括两个系数,一次项系数1和常数项系数4。因此我们每次掷4颗骰子,骰子A,B,C,D,并且把A和B的比值作为一次项系数,C和D的比值作为常数项系数。
而模型2包括三个系数,三次项系数-1/11,二次项系数9/11,和常数项系数23/11。因此我们一次性掷出6颗骰子,骰子A,B,C,D,E,F并且把A和B的比值作为三次项系数,C和D的比值作为二次项系数,E和F的比值作为常数项系数。
好了,交代完毕,现在终于可以掷骰子了。你把这些骰子丢给造物主,让它来掷,我们来看下,它分别掷出模型1和模型2概率是多少。
对于模型1,掷出的A,B骰子的比值为1的概率为 1/101,同样,产生常数项系数4的概率,为 24/101^2(有24种可能的组合可以产生4的比值)。由于这两个系数独立,因此,随机产生一个可以符合h1的模型的概率为
对于模型2,掷出的A,B骰子的比值为三次项系数-1/11的概率为 8/101^2。 掷出的C,D骰子的比值为二次项系数9/11的概率也是8/101^2。掷出的E,F骰子的比值为常数项系数23/11的概率 4/101^2。因此,你掷出6颗骰子一次性可以产生
h2的模型的概率为
因此 P(h1)远远大于P(h2)。换句话说,如果按照上述的方法,造物主通过掷骰子产生模型h1的概率要远远大于h2。这就是为什么我们要选择简单的模型的原因。因为简单的模型,在现实中不常出现。
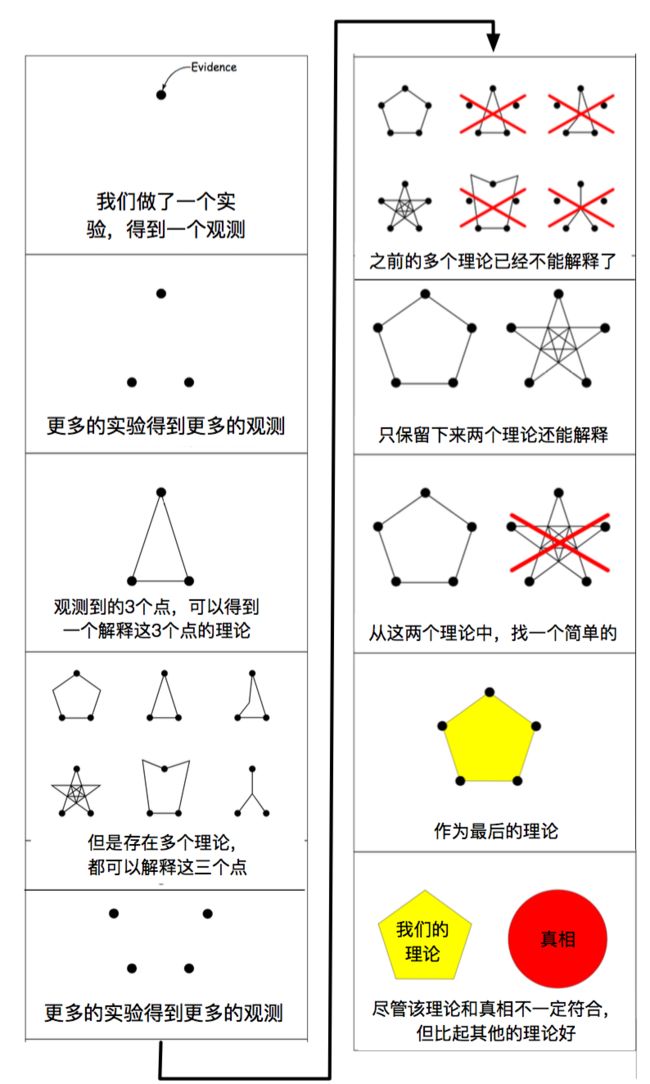
奥卡姆剃刀要求原因可以较好的解释当前的现象。但如果某个原因不能够解释当前的现象时,或者某个原因可以解释过去的现象,但是新的现象无法解释,那我们应该怎么办呢?很简单,我们需要去调整原因,使其同样能够解释当前的现象。同样,在多个可能解释新的现象的原因中,我们找到一个最简单的,作为最后的结果。
我在维基百科上找到了这样一个例子作为本章的结束(见下图),这个例子也在松鼠同学会上被引用过。
总结
- 奥卡姆剃刀:如非必需,勿增实体。
- 奥卡姆剃刀可以用贝叶斯定理来解释:Keep it simple 意味着先验概率大; Not simpler,意味着这 个原因仍然需要能够解释当前的观测。
- 奥卡姆剃刀,是贝叶斯定理的一种特殊情况。奥卡姆剃刀告诉我们,在多个有相同的解释力的原因中要选出一个简单的;而贝叶斯定理不仅仅可以解释奥卡姆剃刀,而且告诉我们更一般的情况,即在解释力和复杂性中找到最好的平衡。