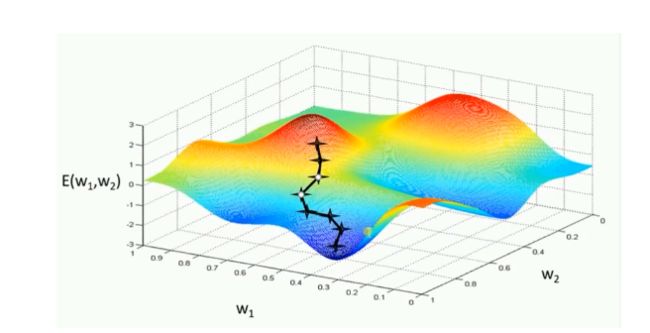
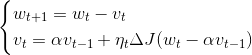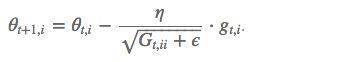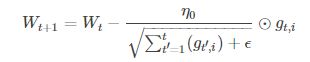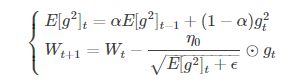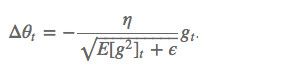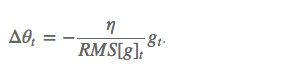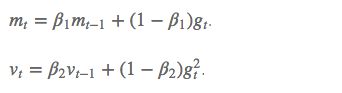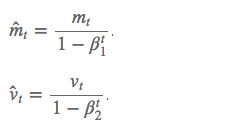一、什么是优化器
优化器或者优化算法,是通过训练优化参数,来最小化(最大化)损失函数。损失函数是用来计算测试集中目标值Y的真实值和预测值的偏差程度。
为了使模型输出逼近或达到最优值,我们需要用各种优化策略和算法,来更新和计算影响模型训练和模型输出的网络参数。
二、优化算法类别
-
一阶优化算法
这种算法使用各参数的梯度值来最小化或最大化损失函数E(x)。最常用的一阶优化算法是梯度下降。
函数梯度:导数dy/dx的多变量表达式,用来表示y相对于x的瞬时变化率。往往为了计算多变量函数的导数时,会用梯度取代导数,并使用偏导数来计算梯度。梯度和导数之间的一个主要区别是函数的梯度形成了一个多维变量。因此,对单变量函数,使用导数来分析;而梯度是基于多变量函数而产生的。
-
二阶优化算法
二阶优化算法使用了二阶导数(也叫做Hessian方法)来最小化或最大化损失函数。这种方法是二阶收敛,收敛速度快,但是由于二阶导数的计算成本很高,所以这种方法并没有广泛使用。
主要算法:牛顿法和拟牛顿法(Newton's method & Quasi-Newton Methods)
牛顿法和梯度下降法的效率对比
三、神经网络优化算法
-
梯度下降GD(Gradient Descent)
梯度下降:学习训练的模型参数为w,损失函数为J(w),则损失函数关于模型参数的偏导数即相关梯度为ΔJ(w),学习率为η,梯度下降法更新参数公式:w=w−η×ΔJ(w),模型参数的调整沿着梯度方向不断减小的方向最小化损失函数。
GD的两个缺点:
(1)训练速度慢:每进行一步都要计算调整下一步方向,在大型数据中,每个样本都更新一次参数,且每次迭代要遍历所有样本,需要很长时间进行训练和达到收敛。
(2)易陷入局部最优解:在有限的范围内寻找路径,当陷入相对较平的区域,误认为最低点(局部最优即鞍点),梯度为0,不进行参数更新。
-
批量梯度下降BGD
批量梯度下降BGD:学习训练样本的总数为n,每次样本i为(x,y),模型参数为w,代价函数为J(w),每个样本i的代价函数关于W的梯度为ΔJ(w,x,y),学习率η,更新参数表达式为:
#下面实现的是批量梯度下降法
def batchGradientDescent(x, y, theta, alpha, m, maxIterations):
xTrains = x.transpose() #得到它的转置
for i in range(0, maxIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis - y
# print loss
gradient = np.dot(xTrains, loss) / m #对所有的样本进行求和,然后除以样本数
theta = theta - alpha * gradient
return theta
优点:到BGD迭代的次数相对较少。
缺点:每一次的参数更新都用到了所有的训练数据(比如有m个,就用到了m个),如果训练数据非常多的话,是非常耗时的。
-
随机梯度下降SGD(Stochastic Gradient Descent)
与BGD最大的区别就在于,更新参数的时候,并没有将所有训练样本考虑进去,然后求和除以总数,而是任取一个样本点,然后利用这个样本点进行更新。更新参数表达式为:
#下面实现的是随机梯度下降法
def StochasticGradientDescent(x, y, theta, alpha, m, maxIterations):
data = []
for i in range(10):
data.append(i)
xTrains = x.transpose() #变成3*10,没一列代表一个训练样本
# 这里随机挑选一个进行更新点进行即可(不用像上面一样全部考虑)
for i in range(0,maxIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis - y #注意这里有10个样本的,我下面随机抽取一个进行更新即可
index = random.sample(data,1) #任意选取一个样本点,得到它的下标,便于下面找到xTrains的对应列
index1 = index[0] #因为回来的时候是list,我要取出变成int,更好解释
gradient = loss[index1]*x[index1] #只取这一个点进行更新计算
theta = theta - alpha * gradient.T
return theta
优点:计算梯度快,对于小噪声,SGD可以很好收敛。对于大型数据,训练很快,从数据中取大量的样本算一个梯度,更新一下参数。
缺点:噪音较BGD要多,权值更新方向可能出现错误,使得SGD并不是每次迭代都向着整体最优化方向。
-
小批量梯度下降法MBGD(Min-Batch)
小批量梯度下降法是为了解决批梯度下降法的训练速度慢,以及随机梯度下降法的准确性综合而来。小批量随机梯度下降法的实现是SGD的基础上,随机取batch个样本,而不是1个样本。但是不同问题的batch是不一样的,没有绝对的取值定义。
动量优化算法在梯度下降法的基础上进行改进,具有加速梯度下降的作用。
-
动量优化算法——Momentum
Momentum:引入一个累计历史梯度信息动量加速SGD。优化公式如下:
alpha代表动量大小,一般取为0.9(表示最大速度10倍于SGD)。当前权值的改变受上一次改变的影响,类似加上了惯性。
动量解决SGD的两个问题:(1)SGD引入的噪声(2)Hessian矩阵病态(SGD收敛过程的梯度相比正常来回摆动幅度较大)。使网络能更优和更稳定的收敛,减少振荡过程。
当我们将一个小球从山上滚下来时,没有阻力的话,它的动量会越来越大,但是如果遇到了阻力,速度就会变小。加入的这一项,可以使得梯度方向不变的维度上速度变快,梯度方向有所改变的维度上的更新速度变慢,这样就可以加快收敛并减小震荡。
缺点:这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚,如果它能具备一些先知,例如快要上坡时,就知道需要减速了的话,适应性会更好。
-
动量优化算法——NAG(Nesterov Accelerated Gradient)
NAG:牛顿加速梯度算法是Momentum变种,更新公式如下:
NAG的计算在模型参数施加当前速度之后,可以理解为在Momentum 中引入了一个校正因子。
在Momentum中,小球会盲目的跟从下坡的梯度,易发生错误。因此,需要提前知道下降的方向,同时,在快到目标点时速度会有所下降,以不至于超出。
NAG用w−alpha*v_{t−1} 来近似当做参数下一步会变成的值,则在计算梯度时,不是在当前位置,而是未来的位置上。(NAG在Tensorflow中与Momentum合并在同一函数tf.train.MomentumOptimizer中,可以通过参数配置启用。)
自适应学习率优化算法:传统的优化算法将学习率设置为常数或者根据训练次数调节学习率。忽略了学习率其他变化的可能性。
-
自适应学习率优化算法——AdaGrad
Adagrad方法是通过参数来调整合适的学习率η,对稀疏参数(低频)进行大幅更新和对频繁参数(高频)进行小幅更新。因此,Adagrad方法非常适合处理稀疏数据,很好地提高了 SGD 的鲁棒性。
Adagrad缩放每个参数反比于其所有梯度历史平均值总和的平方根。具有代价函数最大梯度的参数相应的有快速下降的学习率,而小梯度的参数在学习率上有相对较小的下降。
G_t 是个对角矩阵, (i,i) 元素就是 t 时刻参数 θ_i 的梯度平方和。
Adagrad 的优点是减少了学习率的手动调节,一般 η 就取 0.01。
缺点: 它的缺点是分母会不断积累,这样学习率就会收缩并最终会变得非常小
-
自适应学习率优化算法——RMSprop
修改了AdaGrad的梯度累积为指数加权的移动平均,使在非凸下效果更好。
E[g^2]_t代表前t次的梯度平方的均值。RMSProp的分母取了加权平均,避免学习率越来越低,同时可以自适应调节学习率。
-
自适应学习率优化算法——Adadelta
这个算法是对 Adagrad 的改进,和 Adagrad 相比,就是分母的 G 换成了过去的梯度平方的衰减平均值,指数衰减平均值
这个分母相当于梯度的均方根 root mean squared (RMS) ,所以可以用 RMS 简写:
其中 E 的计算公式如下,t 时刻的依赖于前一时刻的平均和当前的梯度:
梯度更新规则:此外,还将学习率 η 换成了 RMS[Δθ],这样的话,我们甚至都不需要提前设定学习率了:
评价:在训练的前中期,表现效果较好,加速效果可以,训练速度更快。在后期,模型会反复地在局部最小值附近抖动。
-
自适应学习率优化算法——Adam(adaptive moment estimation)
这个算法是另一种计算每个参数的自适应学习率的方法。相当于 RMSprop + Momentum。
除了像 Adadelta 和 RMSprop 一样存储了过去梯度的平方 v_t 的指数衰减平均值 ,也像 momentum 一样保持了过去梯度 m_t 的指数衰减平均值:
如果 m_t 和 v_t 被初始化为 0 向量,那它们就会向 0 偏置,所以做了偏差校正,通过计算偏差校正后的 mt 和 vt 来抵消这些偏差:
梯度更新规则:
m_t和v_t分别维一阶动量和二阶动量,超参数设定值: β1 = 0.9,β2 = 0.999,ϵ = 10e−8
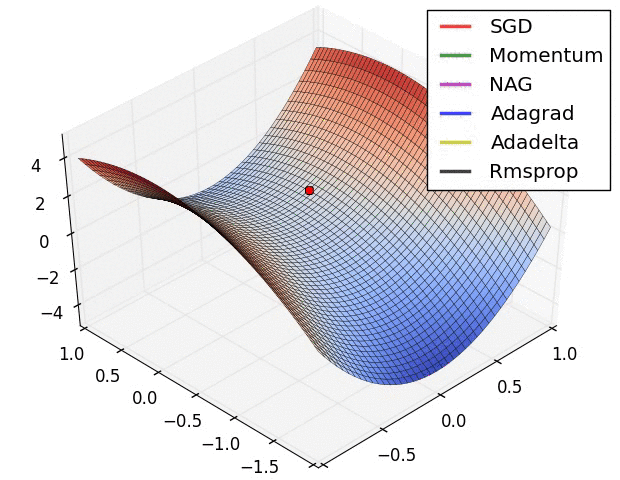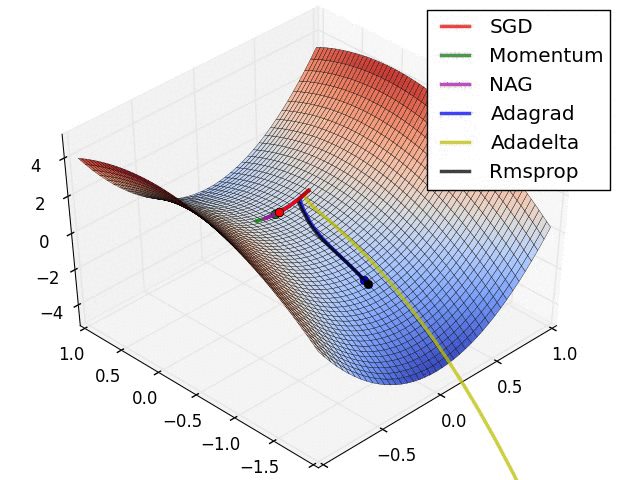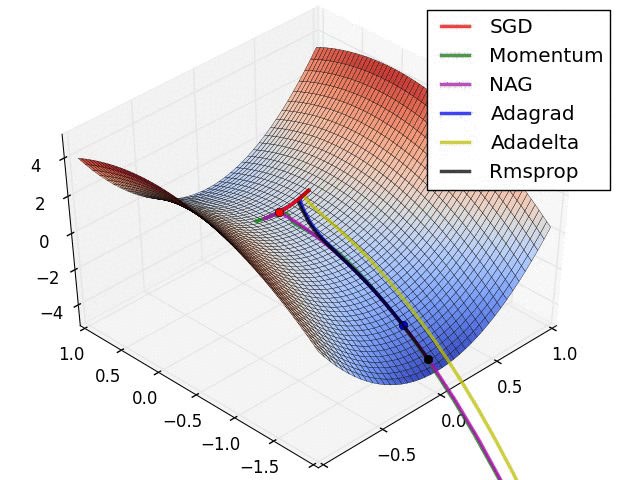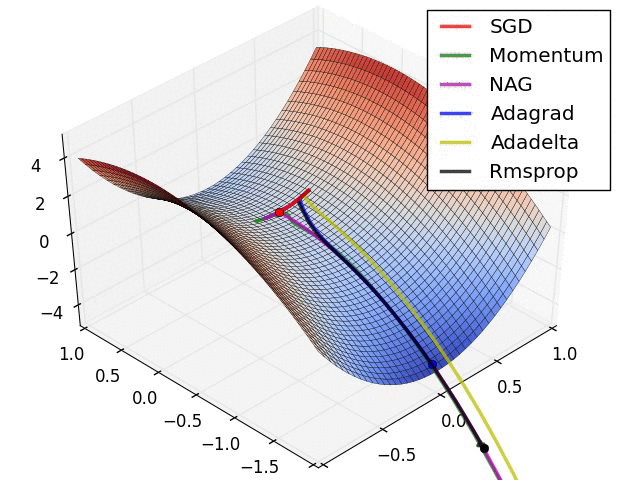
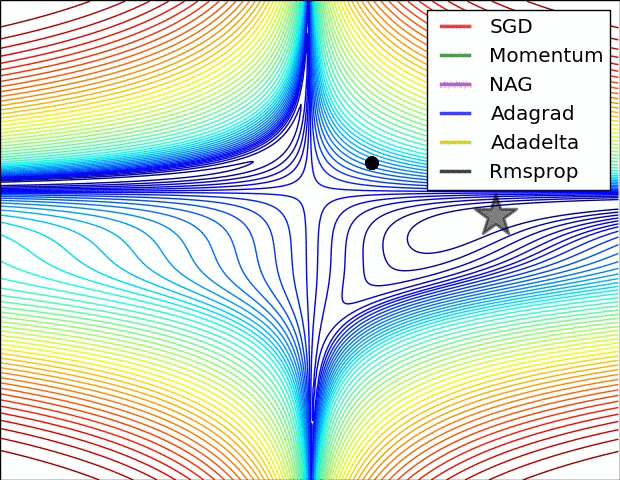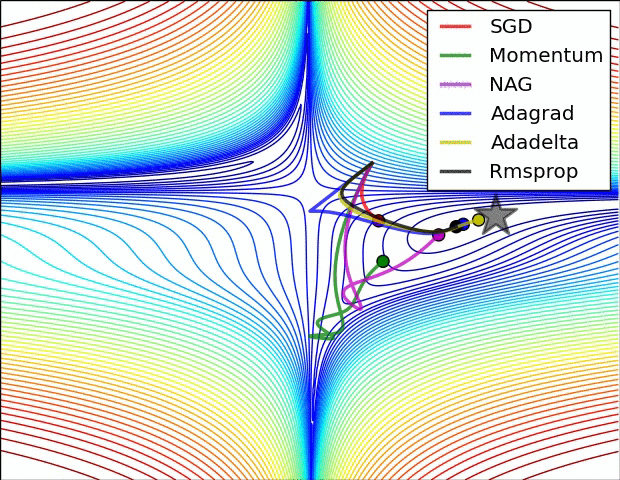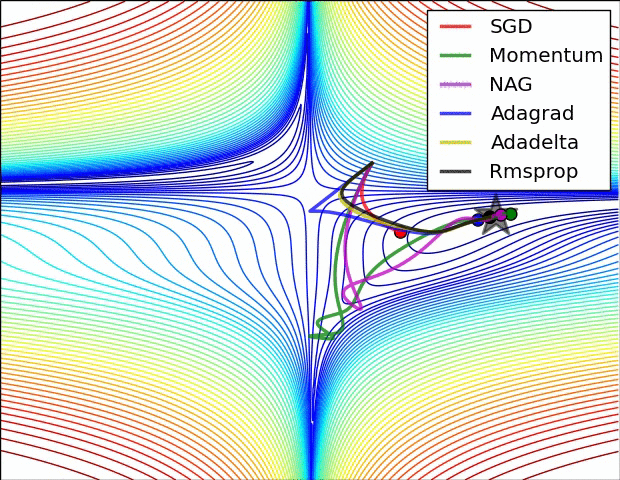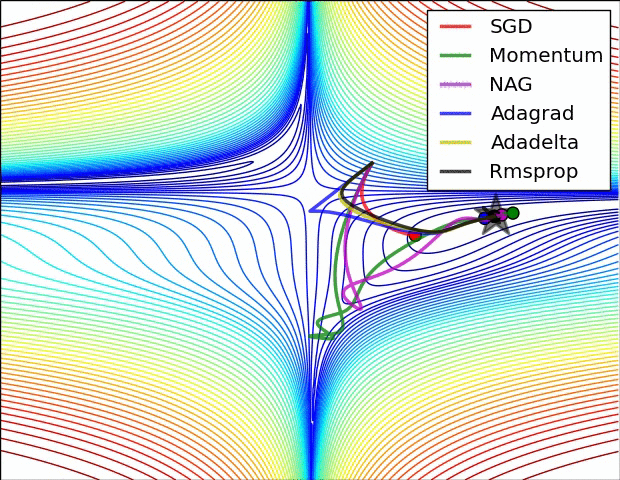
四、优化效果
下几种算法在鞍点和等高线上的表现:
上面两种情况都可以看出,Adagrad, Adadelta, RMSprop 几乎很快就找到了正确的方向并前进,收敛速度也相当快,而其它方法要么很慢,要么走了很多弯路才找到。
但是,自适应优化算法通常都会得到比SGD算法性能更差(经常是差很多)的结果,尽管自适应优化算法在训练时会表现的比较好,因此使用者在使用自适应优化算法时需要慎重考虑!(CVPR的paper全都用的SGD,而不是用理论上的Adam)