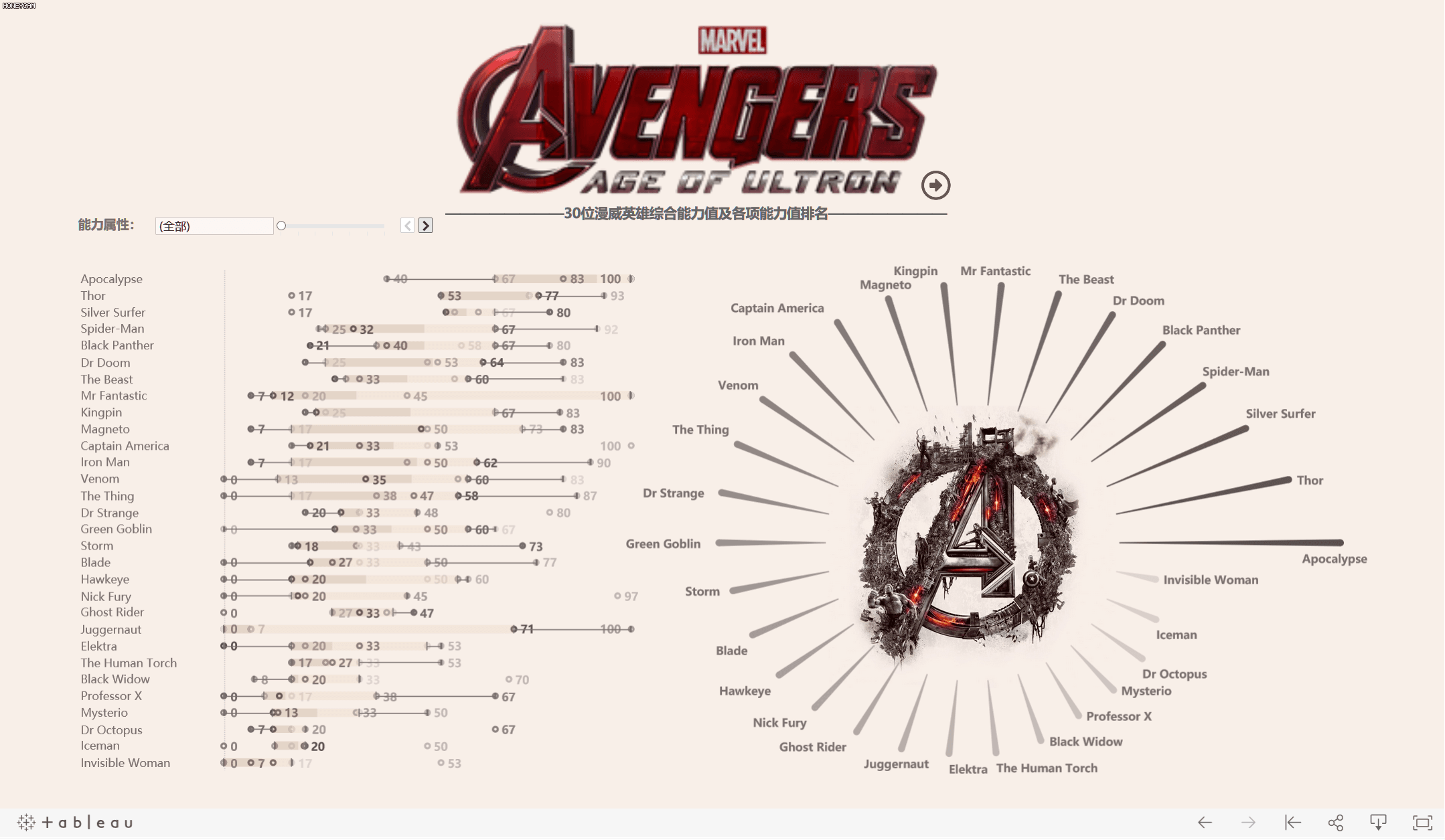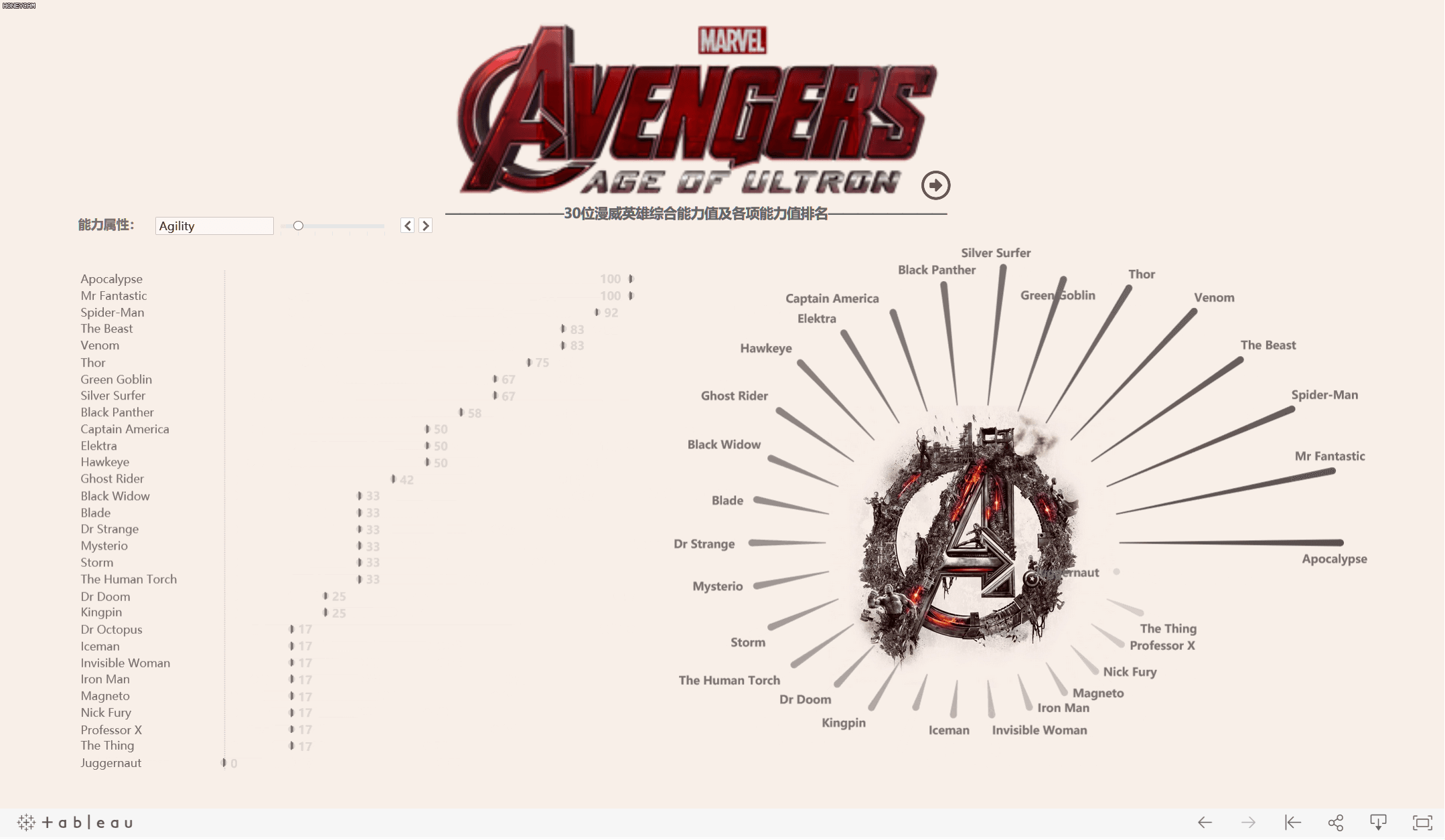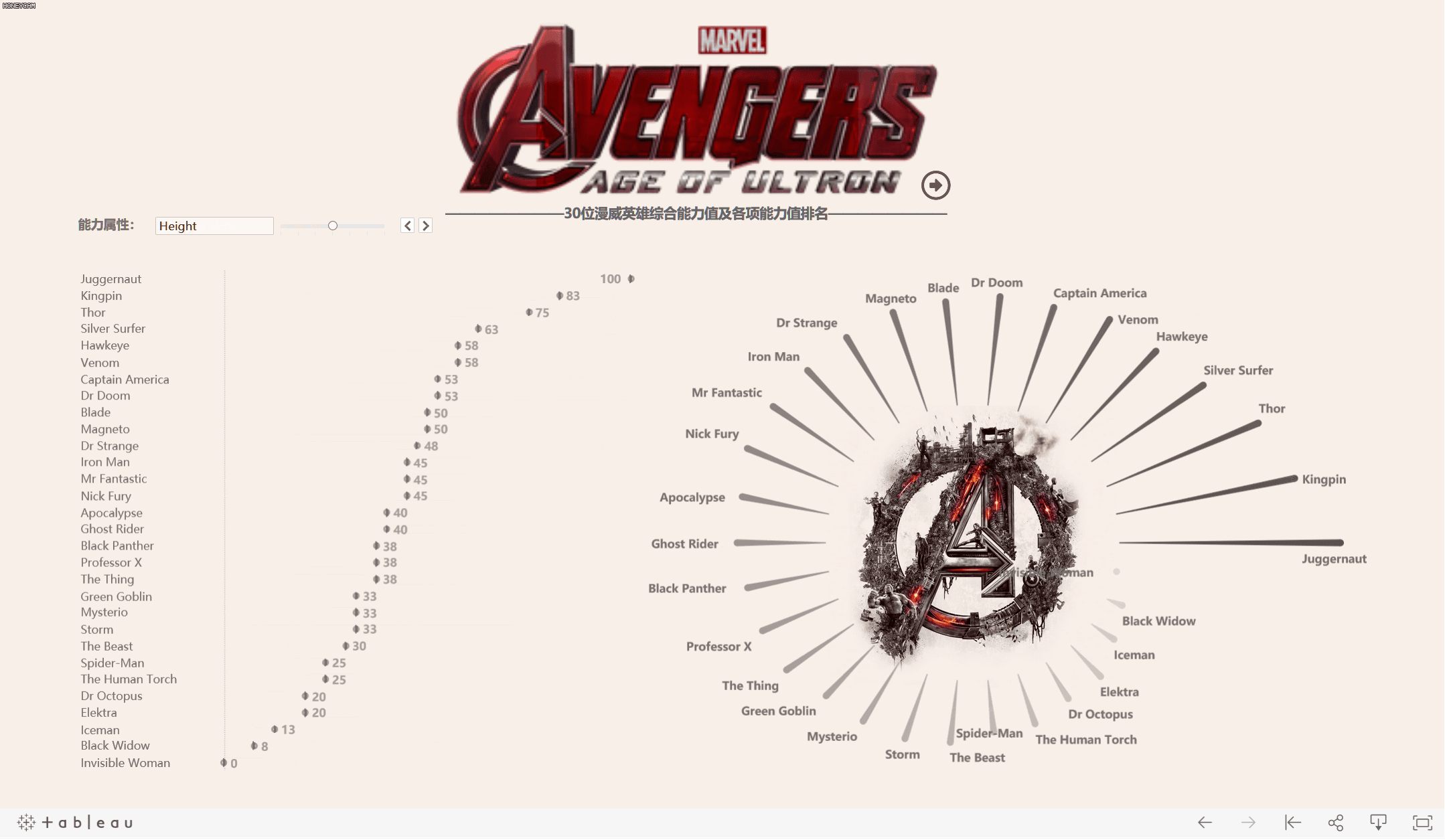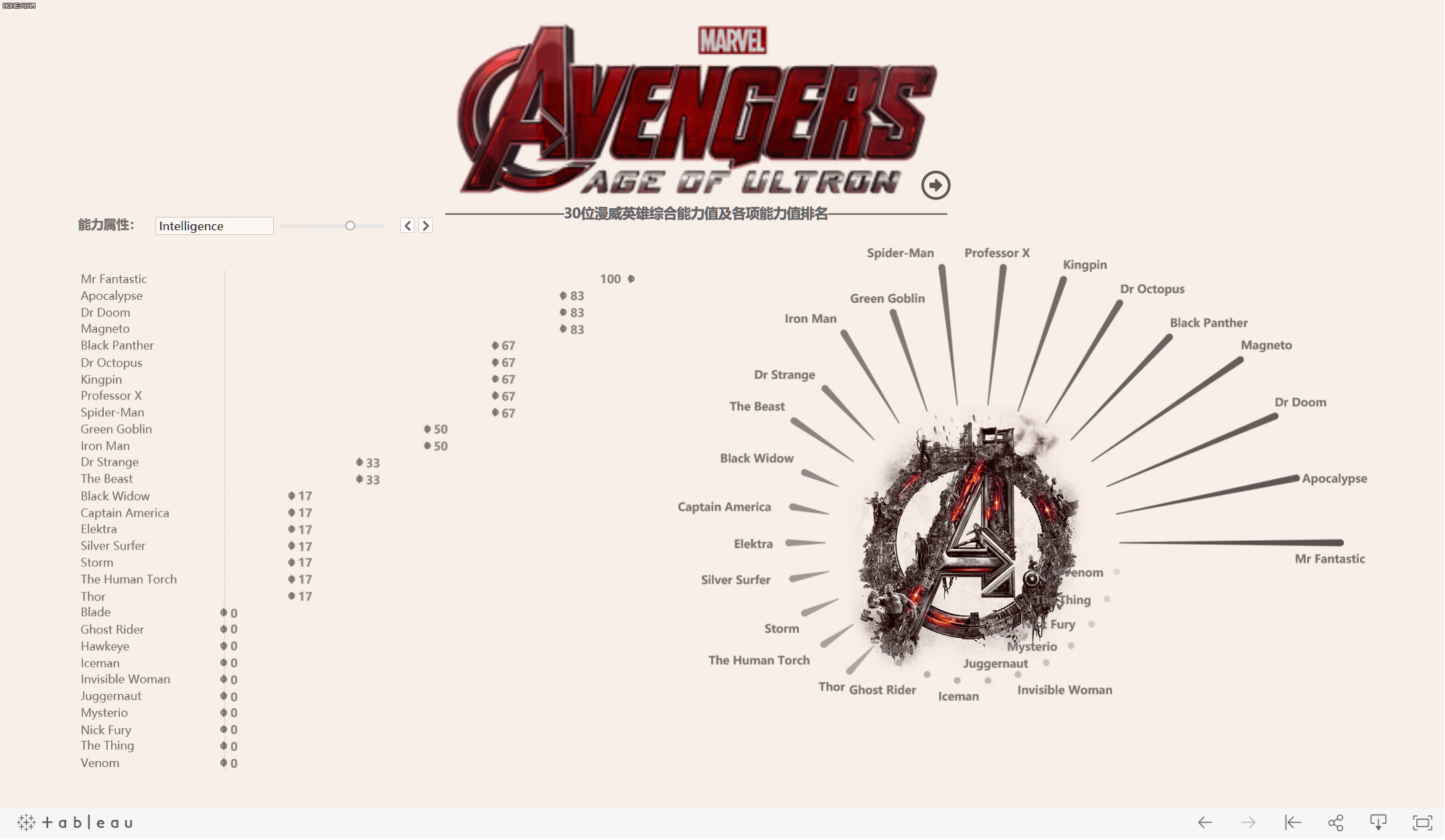
工作簿在此:Tableau Public: Marvel_SuperHeros
这次主要挑战了一下Tableau制作雷(zhen)达(ma)图(fan)和放射条形图!!!
不过还是硬着头皮死磕到底。。。所幸最后总算成功了,效果还算满意~~~
整个流程分三步:
观察数据 > 数据预处理 > 可视化
数据准备阶段,Python小白顺便拿这次的数据练练手
一、观察/理解数据
import numpy as np
import pandas as pd
df=pd.read_csv('Superheroes.csv')
df.head()
| Name | Attribute Name | Gender | Value | |
|---|---|---|---|---|
| 0 | Black Widow | Agility | 0 | 14 |
| 1 | Elektra | Agility | 0 | 16 |
| 2 | Invisible Woman | Agility | 0 | 12 |
| 3 | Storm | Agility | 0 | 14 |
| 4 | Black Widow | Fighting Skills | 0 | 76 |
#查看一下数据框的详细信息
df.info()
RangeIndex: 180 entries, 0 to 179
Data columns (total 4 columns):
Name 180 non-null object
Attribute Name 180 non-null object
Gender 180 non-null int64
Value 180 non-null int64
dtypes: int64(2), object(2)
memory usage: 8.5+ KB
#看看有多少个英雄
df['Name'].describe()
count 180
unique 30
top Captain America
freq 6
Name: Name, dtype: object
#Attribute Name中的唯一值
list(df['Attribute Name'].unique())
['Agility', 'Fighting Skills', 'Height', 'Intelligence', 'Speed', 'Strength']
#数据透视表来一个
df.pivot_table(index='Name',columns='Attribute Name',values='Value').describe()
| Attribute Name | Agility | Fighting Skills | Height | Intelligence | Speed | Strength |
|---|---|---|---|---|---|---|
| count | 30.000000 | 30.000000 | 30.00000 | 30.000000 | 30.000000 | 30.000000 |
| mean | 15.200000 | 71.233333 | 181.70000 | 4.933333 | 6.000000 | 36.400000 |
| std | 3.397768 | 8.605064 | 8.55066 | 1.964045 | 3.877432 | 15.612992 |
| min | 10.000000 | 55.000000 | 165.00000 | 3.000000 | 1.000000 | 15.000000 |
| 25% | 12.000000 | 64.250000 | 177.25000 | 3.000000 | 3.250000 | 26.000000 |
| 50% | 14.000000 | 71.500000 | 181.00000 | 4.000000 | 4.500000 | 29.500000 |
| 75% | 17.750000 | 77.750000 | 185.75000 | 7.000000 | 8.750000 | 44.750000 |
| max | 22.000000 | 85.000000 | 205.00000 | 9.000000 | 16.000000 | 81.000000 |
- 数据很完整,没有缺失
- 根据这些数据,可以考虑利用雷达图来展现每个超级英雄的能力图谱。
- 根据常识判断,每种能力属性的单位不同,且从最后的透视表结果可以看出,数值范围也有很大差距,因此需要对这些数值进行标准化处理。
Agility:10-22
Fighting Skills:55-85
Height:165-205
Intelligence:3-9
Speed:1-16
Strength:15-81
二、数据预处理
数据没有大问题,跳过数据清洗阶段,直接进入数据加工阶段,这一阶段主要就是进行数据计算,对“Value”这一度量进行标准化处理。
常见的标准化方法有:min-max标准化(Min-max normalization),log函数转换,atan函数转换,z-score标准化(zero-mena normalization,此方法最为常用),模糊量化法。本文只介绍min-max法(规范化方法)。
极差标准化法,是消除变量量纲和变异范围影响最简单的方法。
具体的操作方法为:首先需要找出该指标的最大值(Xmax)和最小值(Xmin),并计算极差(R = Xmax - Xmin),然后用该变量的每一个观察值(X)减去最小值(Xmin),再除以极差(R),即:X' = (X-Xmin) / (Xmax-Xmin)
经过极差标准化方法处理后,无论原始数据是正值还是负值,该变量各个观察值的数值变化范围都满足0≤X'≤1,并且正指标、逆指标均可转化为正向指标,作用方向一致。但是如果有新数据加入,就可能会导致最大值(Xmax)和最小值(Xmin)发生变化,就需要进行重新定义,并重新计算极差(R)。
用Python进行标准化计算:(Python小白想不出好的写法了,先将就着用用)
#从透视表里提取每个能力值的max和min
mm=df.pivot_table(index='Name',columns='Attribute Name',values='Value').describe()
df['V_N']=None
bool=(df['Attribute Name']=='Agility')
df['V_N'][bool]=df.Value[bool].apply(lambda x: (x-mm['Agility']['min'])/(mm['Agility']['max']-mm['Agility']['min']))
bool=(df['Attribute Name']=='Fighting Skills')
df['V_N'][bool]=df.Value[bool].apply(lambda x: (x-mm['Fighting Skills']['min'])/(mm['Fighting Skills']['max']-mm['Fighting Skills']['min']))
bool=(df['Attribute Name']=='Height')
df['V_N'][bool]=df.Value[bool].apply(lambda x: (x-mm['Height']['min'])/(mm['Height']['max']-mm['Height']['min']))
bool=(df['Attribute Name']=='Intelligence')
df['V_N'][bool]=df.Value[bool].apply(lambda x: (x-mm['Intelligence']['min'])/(mm['Intelligence']['max']-mm['Intelligence']['min']))
bool=(df['Attribute Name']=='Speed')
df['V_N'][bool]=df.Value[bool].apply(lambda x: (x-mm['Speed']['min'])/(mm['Speed']['max']-mm['Speed']['min']))
bool=(df['Attribute Name']=='Strength')
df['V_N'][bool]=df.Value[bool].apply(lambda x: (x-mm['Strength']['min'])/(mm['Strength']['max']-mm['Strength']['min']))
df.head(10)
#算个百分制,看着比较舒服
df['V_N*100']=df['V_N'].apply(lambda x: round(x*100))
df.head()
| Name | AttributeName | Gender | Value | V_N | V_N*100 | |
|---|---|---|---|---|---|---|
| 0 | Black Widow | Agility | 0 | 14 | 0.333333 | 33 |
| 1 | Elektra | Agility | 0 | 16 | 0.500000 | 50 |
| 2 | Invisible Woman | Agility | 0 | 12 | 0.166667 | 17 |
| 3 | Storm | Agility | 0 | 14 | 0.333333 | 33 |
| 4 | Black Widow | Fighting Skills | 0 | 76 | 0.700000 | 70 |
当然简单的方法有很多,我这儿纯粹是练习Python用的,下面进入可视化环节~
三、可视化
Tableau雷达图的制作可以参考这里:用Tableau画雷达图
放射条形图可以参考这个:用花型射线图 Radial Chart 对比数据
磨刀不误砍柴功——弄清楚基本概念
有时候总是觉得为什么tableau这么复杂,有些图表连excel都超容易出。很多时候发现自己都在凭感觉作图,而事实上却连最基本的概念“维度”,“度量”,“连续”,“离散”都还没搞清楚。所以,磨刀不误砍柴工,我还是决定自己一边详细地理一理概念,一边总结一下制作步骤。
雷达图
你看的的雷达图不只是一张图,其实是由三张工作表叠加而成
1、同心六边形
构建六边形,关键在于要在直角坐标系中确定六边形6个顶点的位置。
其实就是一道数学题:已知圆心(x0,y0),半径r,角度a,求圆上的点坐标:假设圆上任一点为(x1,y1),则
x1 = x0 + r * cos( a )
y1 = y0 + r * sin( a )
所以在这里我们可以:
-圆心默认为直角坐标系原点(0,0);
-六边形外接圆半径[R]可以自定义;
-6个顶点在圆上的角度分别为:0',60',120',180',240',300',360'
-6个顶点的直角坐标就可以根据以上数据在Tableau中创建以下两个计算字段求得:
· [sin]=SIN([point]PI()/180)[R]
· [cos]=COS([point]PI()/180)[R]
- 构造数据集
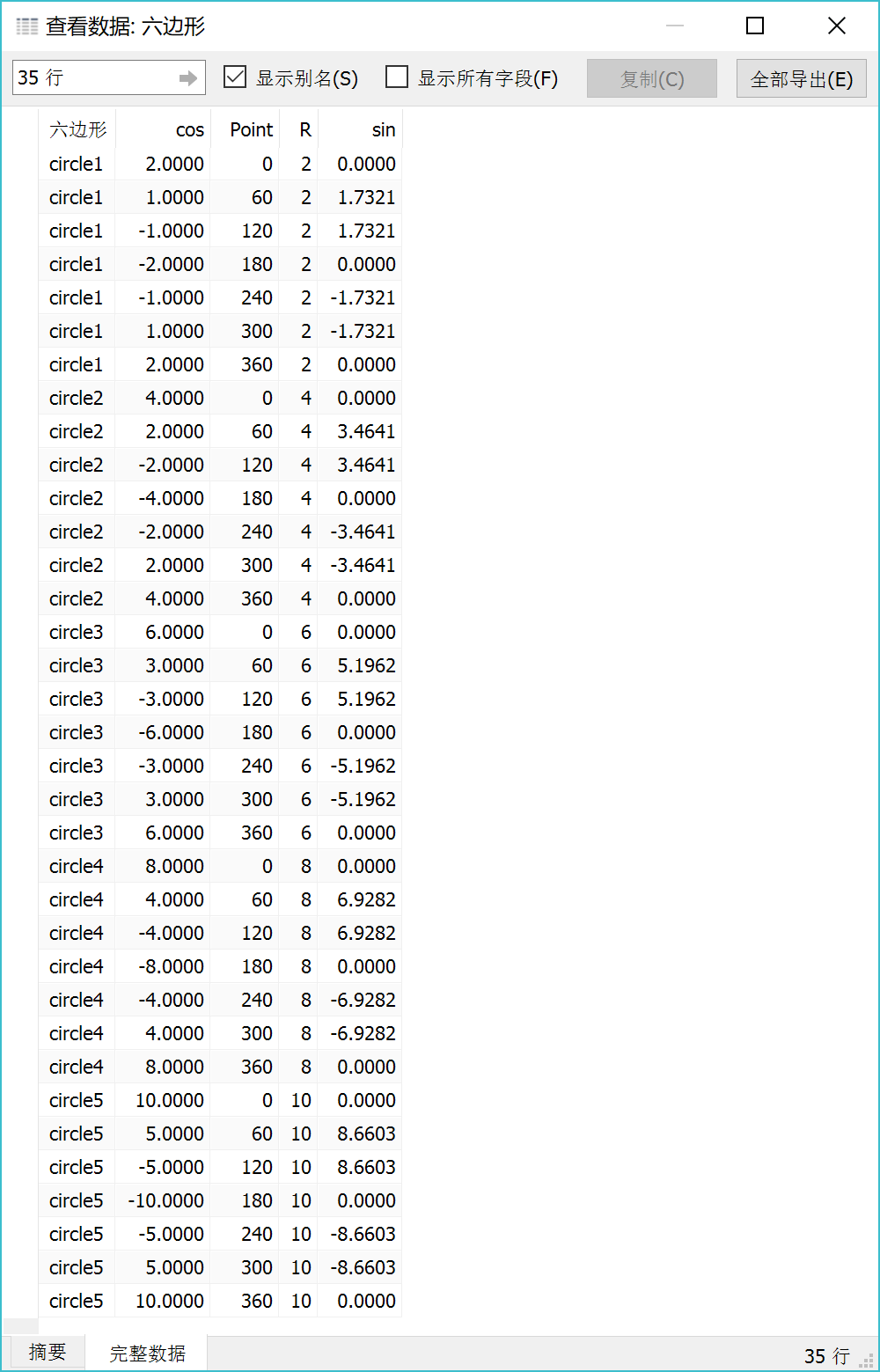
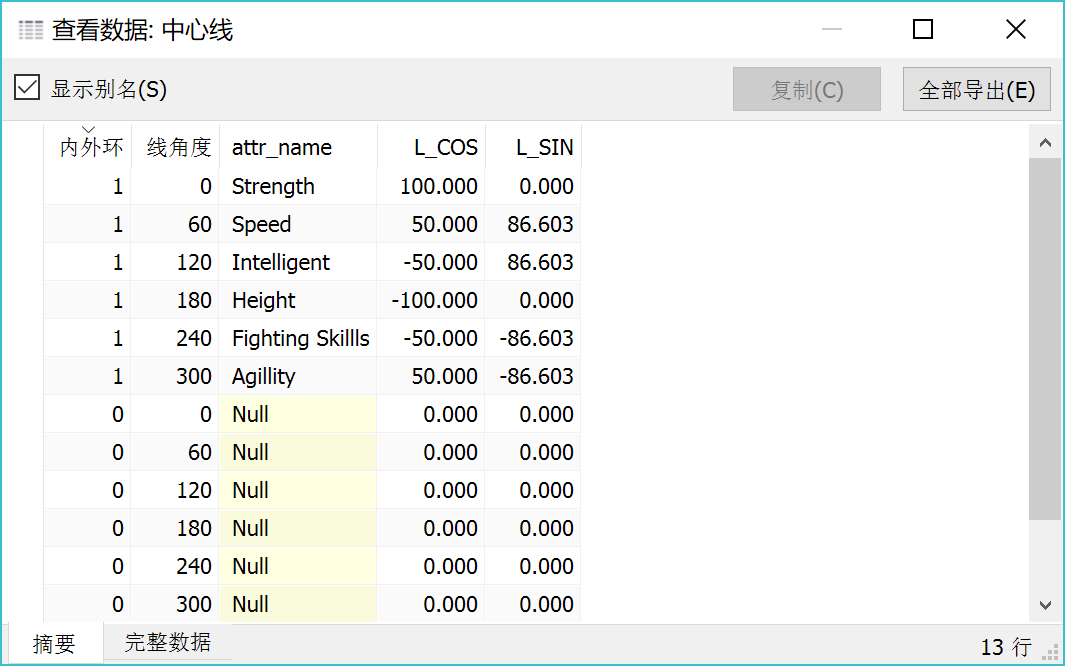
根据以上思路,就可以构造创建同心六边形的数据集了,最终的同心六边形完整的数据集如下图
-
Tableau拖拉拽进行曲
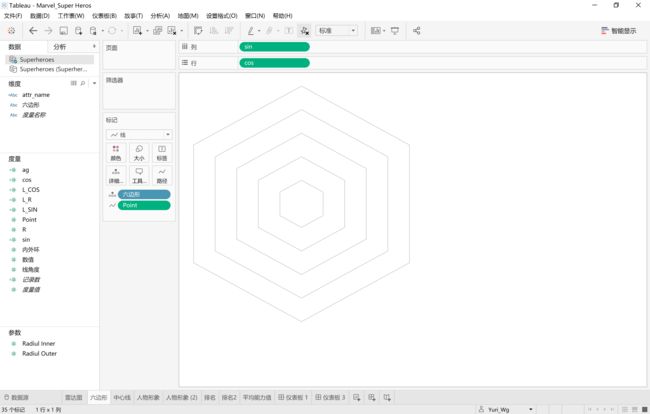
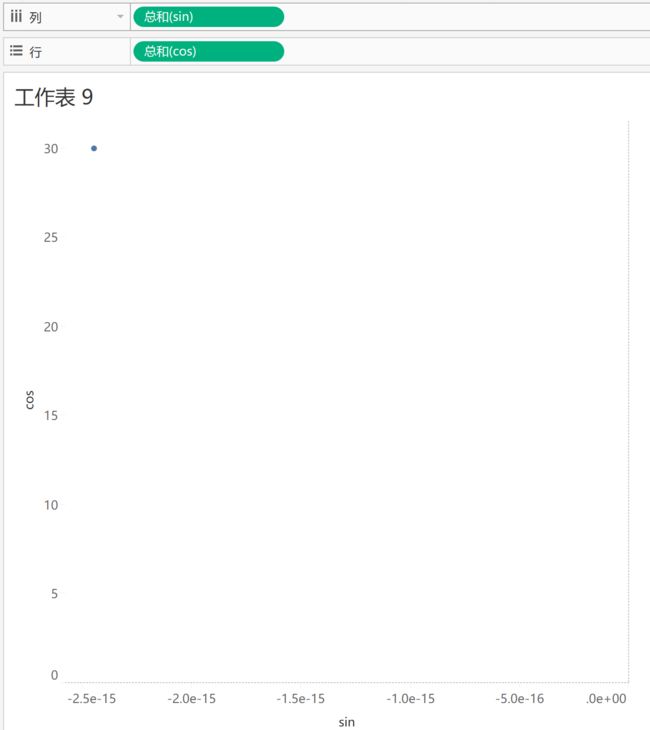
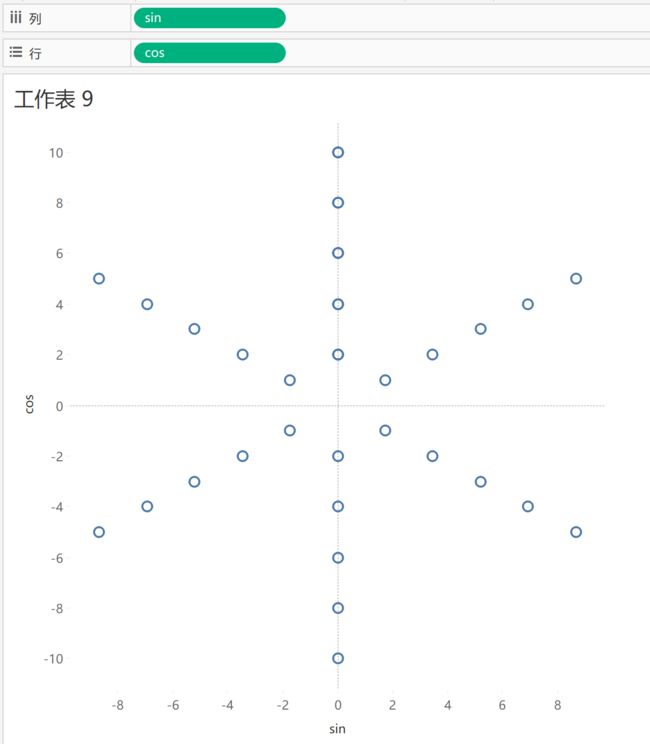
把sin和cos两个度量拖到视图上,出来两个坐标轴和一个点,为什么?
官方文档:
当您第一次连接到数据源时,Tableau 会将包含离散分类信息的任何字段(例如,值为字符串或布尔值的字段)分配给“数据”窗格中的“维度”区域。
当您单击并将字段从“维度”区域拖到“行”或“列”时,Tableau 将创建列或行标题。
当您第一次连接到数据源时,Tableau 会将包含定量数值信息的任何字段(即其中的值为数字的字段)分配给“数据”窗格中的“度量”区域。
当您将字段从“度量”区域拖到“行”或“列”时,Tableau 将创建连续轴。
所以那一点代表了所有点聚合的结果,当然这里我不想要它们聚合,所以这里需要右击sin和cos将其设置成维度。
先将cos设置成维度,可以发现视图发生了变化
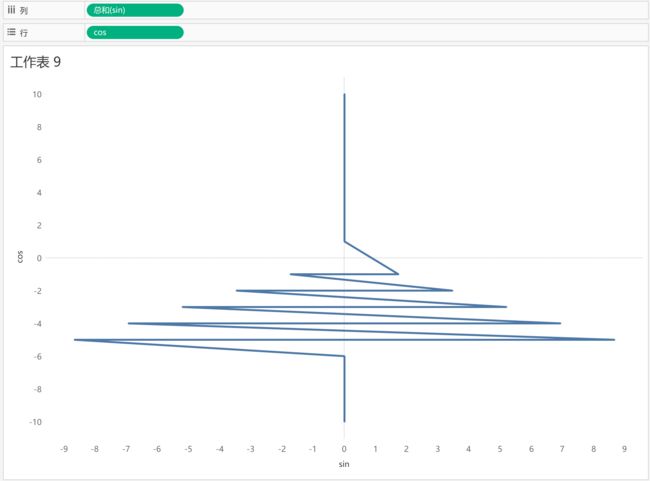
再将sin设置成维度,视图再一次发生了变化,也离同行六边形越来越近了
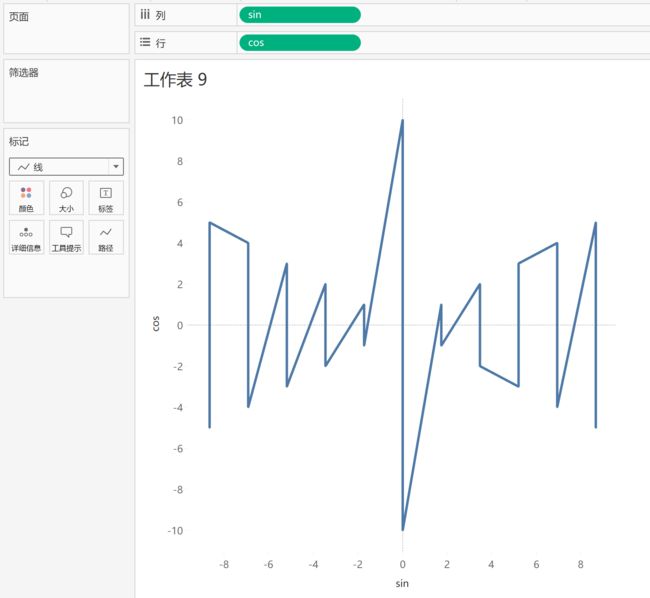
接下去试着把标记类型改为 线条,可以发现所有的点都被视为一个对象连成了一条线
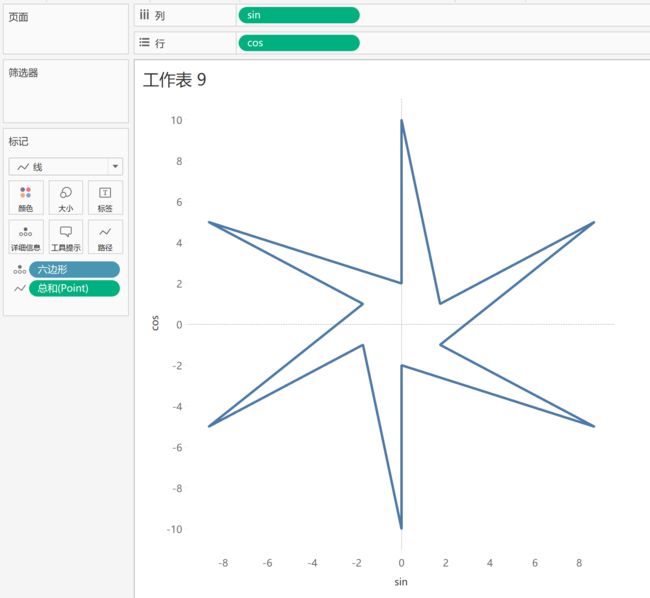
而我们需要的其实是5条独立的线组成的5个六边形,这时候把[六边形]维度拖到标记里,来对每一组顶点予以区分,得到的结果如下图,确实产生了5组独立的连线,但是点之间连接的顺序还有些问题
记得在开始创建数据时有一个[point]字段,依此记录了每一个点的角度值,将它作为标记的 路径拖进来,可以看到[point]默认为聚合,所有点又连成了一个整体
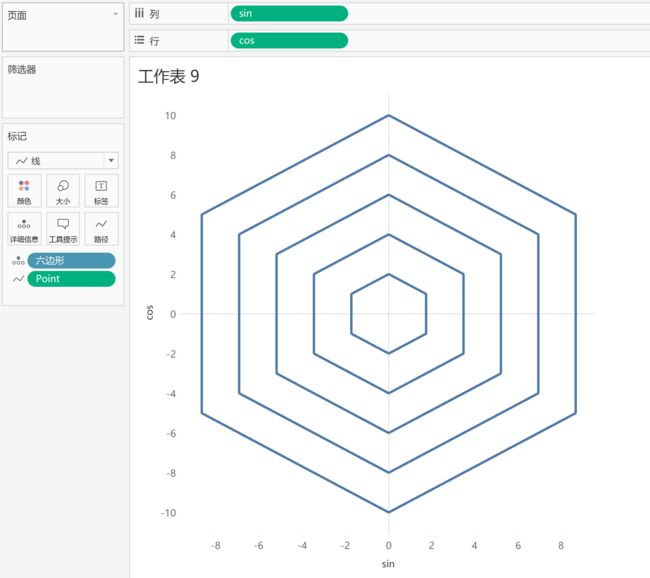
最后一步:将[point]设置为维度,要构造的同心六边形就形成啦~
针对度量和维度,我们了解了基础概念,同时特别要注意的点:
-离散字段创建标题、连续字段创建连续轴
-辨别视图中的字段是度量还是维度的依据在于该字段是否已聚合
-维度和度量是可以相互转化的
-离散字段和连续字段也是可以相互转化的
-维度/度量和离散/连续不是必然对应的
2、放射线
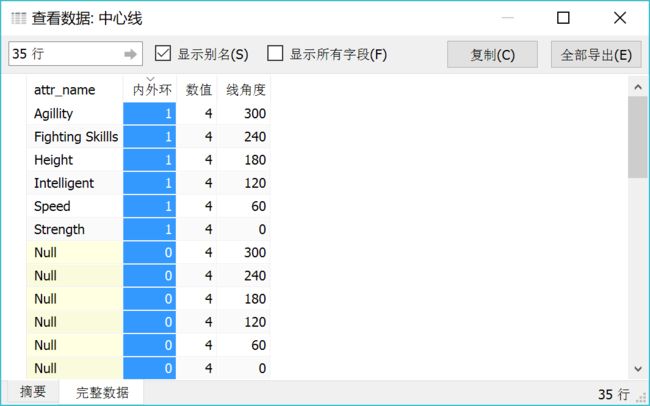
先看一下最终成图以及数据摘要和完整数据
“完整数据”中是需要构建的最原始的数据集,思路跟创建六边形类似
最关键的就是计算弧度和半径R,从而确定几个点的直角坐标
先看一下几个重要的计算字段:
弧度计算
[angle]=2 * PI() * (INDEX()-1) * (1/WINDOW_COUNT(COUNT([数值])))
其实这是个通用公式,在数据量大时尤其好用,构造6条射线这种情境下有点“杀鸡焉用宰牛刀”的感觉,其实大可以这样算2 * PI() * (INDEX()-1) * (1/6)。
但是想要一劳永逸,当然要一开始就突破难点啦~
所以还是不要偷懒,先琢磨透原理吧~
(对了,ps.[数值]列类似于辅助列,数值可以自由设定)
1/WINDOW_COUNT(COUNT([数值]))可以理解为将圆切分成几个等份,每个占据1/6份
(INDEX()-1) * (1/WINDOW_COUNT(COUNT([数值]))),将数值代入看看:
(1-1) * (1/6)=0;
(2-1) * (1/6)=1/6;......
结果依此是:0,1/6,2/6......5/6
2 * PI() * (INDEX()-1) * (1/WINDOW_COUNT(COUNT([数值])))的结果就是得到每个点的弧度半径计算
[R]=IIF(ATTR([内外环])= 0, 0, SUM([数值])/WINDOW_MAX(SUM([数值])))
依然是一个通用公式,适用于构建放射条形图(每条线半径不同的情况),这里也可以简单化处理直接IIF(ATTR([内外环])= 0, 0, 1)
如果是内环,半径为0;
如果是外环,则进行归一化处理,处理后也可以乘以一个系数100,让数字看起来好看一点计算直角坐标
[sin]=SIN([angle]) * [R]
[cos]=COS([angle]) * [R]
造好数据以后就是拖拉拽啦~
(计算字段的命名可能跟图上显示的有些出入,大家意会一下,其实计算字段可以整合的更简单一些,现在有很多冗余,下次改进)
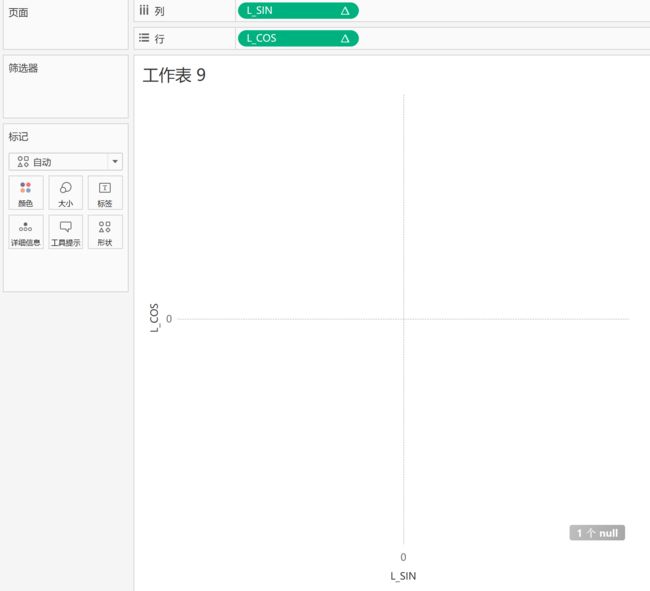
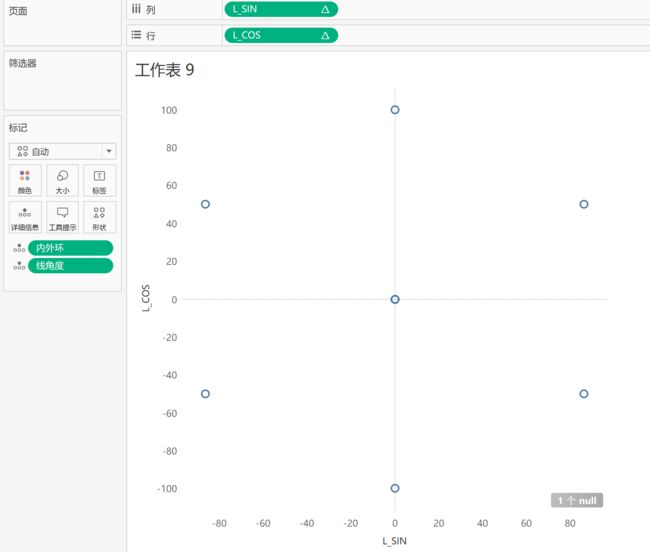
[sin]和[cos]先拽进来,发现是只有一个空值,为什么?
看看半径的计算公式里有个条件判断IIF(ATTR([内外环])= 0, ...)
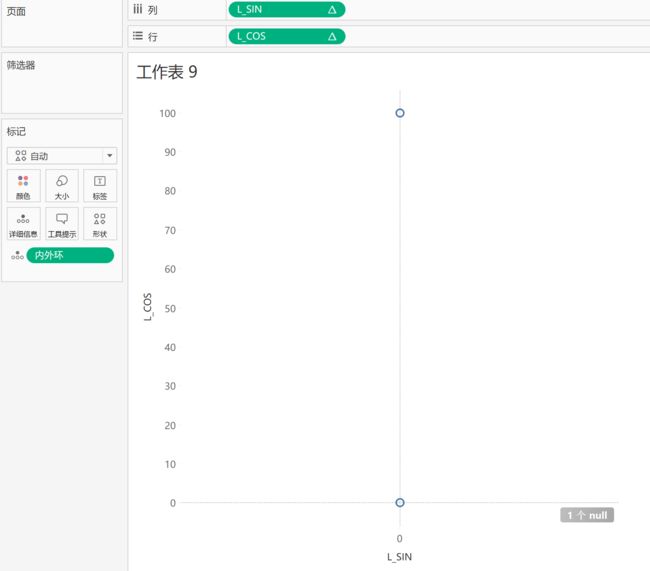
试试把[内外环]拽到标记里并且设置成维度,有动静了~
再把[线角度]拖到标记栏,设置成维度,作为[sin]和[cos]的“计算依据”,这里应该是用到了分区计算的概念 ,提一下
基于“区”的计算
计算依据中的“区”,就是指视图中的子视图或子数据表,在计算时,“区”不像“表”那样贯穿到边(底),而是根据分组,在分组中进行独立计算。
基于“表”的计算
计算依据中的“表”,就是指视图中的整个数据表,不论其计算方向是横向、纵向、横穿然后向下、向下然后横穿中的哪一种,其计算可以理解贯穿到边(底)。
基于“单元格”的计算
最特殊的一种,每个单元格只与自己进行计算,与其它单元格均无联系
点就出来啦~
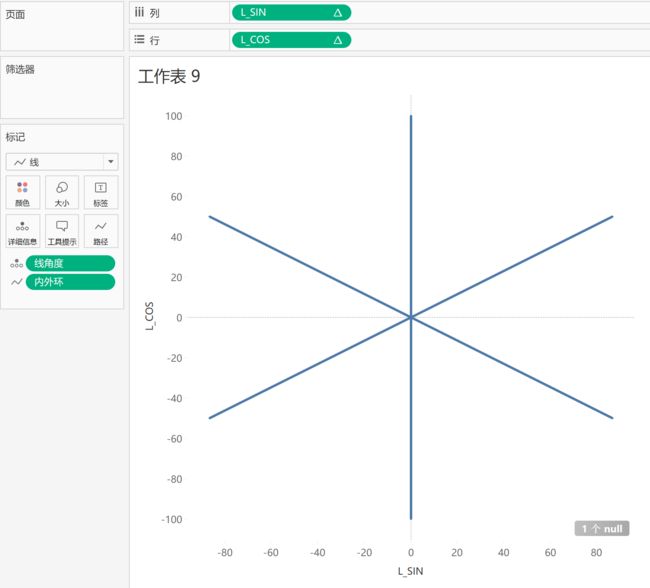
接着把标记类型改为“线”,再把[内外环]作为路径依据,6条线就出来啦~
3、面积图(不规则六边形)
开始造吧!
目标依旧是计算得到每个点的直角坐标
- 创建计算字段
确定径向角:
[Angel]=(INDEX()-1) * (1/WINDOW_COUNT(COUNT([Radial Field])))2PI()
**注:这里的[Radial Field]可以根据不同的可视化项目代入不同数据,这里我们要用到之前我们标准化处理后的能力值 [Value_N * 100]
确定半径:
[radial normalized length]=[Radiul Inner]+IIF(ATTR([Path])=0,0,SUM([Radiul Field])/WINDOW_MAX(SUM([Radiul Field])) * ([Radiul Outer]-[Radiul Inner]))
参数:[radial inner]、[radial outer]
这个应该算是增强版的径向长度通用计算公式,和之前的半径计算公式
[R]=IIF(ATTR([内外环])= 0, 0, SUM([数值])/WINDOW_MAX(SUM([数值])))是一个原理,只是增加了两个参数内径和外径,更适用于放射条形图~
弄懂原理以后,自己可以简化一下,比如:
[radial normalized length]=SUM([Radiul Field])/WINDOW_MAX(SUM([Radiul Field]))
计算(x,y)
[radial x]=[radial normalized length] * COS([Radial Angel])
[radial y]=[radial normalized length] * SIN([Radial Angel])
接着进行拖拉拽
依旧是[radial x],[radial y]先登场,再把[Attribute Name]拽进来作为分区计算的依据
罗列一下用到的几个函数:
1、数字函数:
PI( ):返回数字常量 pi:3.14159。
SIN(number):返回角度的正弦。以弧度为单位指定角度。
COS(number):返回角度的余弦。以弧度为单位指定角度。
示例:COS(PI( ) /4)
2、聚合函数:
ATTR(expression):如果它的所有行都有一个值,则返回该表达式的值。否则返回星号。会忽略 Null 值。
COUNT(expression):返回组中的项目数。不对 Null 值计数。
SUM(expression):返回表达式中所有值的总计。SUM 只能用于数字字段。会忽略 Null 值。
3、逻辑函数:
IIF(test, then, else, [unknown]):检查某个条件是否得到满足,如果为 TRUE 则返回一个值,如果为 FALSE 则返回另一个值,如果未知,则返回可选的第三个值或 NULL。
4、表计算函数:
INDEX( ):返回分区中当前行的索引,不包含与值有关的任何排序。第一个行索引从 1 开始。
WINDOW_COUNT(expression, [start, end]):返回窗口中表达式的计数。窗口用与当前行的偏移定义。使用 FIRST()+n 和 LAST()-n 表示与分区中第一行或最后一行的偏移。如果省略了开头和结尾,则使用整个分区。
WINDOW_SUM(expression, [start, end]):返回窗口中表达式的总计。窗口用与当前行的偏移定义。使用 FIRST()+n 和 LAST()-n 表示与分区中第一行或最后一行的偏移。如果省略了开头和结尾,则使用整个分区。
偷个小懒,回补~