Best Time to Buy and Sell Stock
https://leetcode.com/problems/best-time-to-buy-and-sell-stock/Best Time to Buy and Sell Stock II
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/Best Time to Buy and Sell Stock III
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii/
最多两次交易,pre,post,遍历Best Time to Buy and Sell Stock IV
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv/
最多k次交易Best Time to Buy and Sell Stock with Cooldown
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/
1天的cooldown
待补充:
k次交易+cooldown
后两题使用local,global数组而非buy,sell数组进行dp。
1 一次交易
class Solution {
public:
int maxProfit(vector& prices) {
int n = prices.size();
int res = 0;
int low = INT_MAX;
for(int i = 0; i < n; i++) {
if(prices[i] < low)
low = prices[i];
res = max(res, prices[i] - low);
}
return res;
}
};
2 任意多次交易
class Solution {
public:
int maxProfit(vector& prices) {
int res = 0;
int n = prices.size();
for(int i = 0; i < n; i++) {
if(i > 0 && prices[i] > prices[i-1])
res += prices[i] - prices[i-1];
}
return res;
}
};
3 两次交易
class Solution {
public:
int maxProfit(vector& prices) {
int n = prices.size();
vector pre(n); //sell before/at ith day
vector post(n);//buy after/at ith day
//pre
int low = INT_MAX;
int res = 0;
for(int i = 0; i < n; i++) {
if(prices[i] < low)
low = prices[i];
res = max(res, prices[i] - low);
pre[i] = res;
}
//post
int high = INT_MIN;
res = 0;
for(int i = n - 1; i >= 0; i--) {
if(prices[i] > high)
high = prices[i];
res = max(res, high - prices[i]);
post[i] = res;
}
res = 0;
for(int i = 0; i < n; i++) {
res = max(res, pre[i] + post[i]);
}
return res;
}
};
4 k次交易
class Solution {
public:
int maxProfit(int k, vector &prices) {
int len = prices.size();
if (len<2) return 0;
int n = prices.size();
//stock ii
if(k >= n/2) {
int ans = 0;
for(int i = 1; i < n; i++) {
ans += max(0, prices[i] - prices[i-1]);
}
return ans;
}
//dp
int local[n][k+1]={};
int global[n][k+1]={};
for(int j = 1; j <= k; j++) {
for(int i = 1; i < n ; i++) {
int diff = prices[i] - prices[i-1];
local[i][j] = max(local[i-1][j] + diff, global[i-1][j-1] + max(diff, 0));
global[i][j] = max(global[i-1][j], local[i][j]);
}
}
return global[n-1][k];
}
};
这样效果一样:
local两种情况:第i-1天之前买入,第i-1天买入。
local[i][j] = max(local[i-1][j] + diff, global[i-1][j-1] + diff);
global[i][j] = max(max(global[i-1][j-1],global[i-1][j]), local[i][j]);
一维dp,第二层反向遍历:
vector local(k+1,0);
vector global(k+1,0);
for(int i = 1; i < n ; i++) {
for(int j = k; j >= 1; j--) {
int diff = prices[i] - prices[i-1];
local[j] = max(local[j] + diff, global[j-1] + diff);
global[j] = max(max(global[j-1],global[j]), local[j]);
}
}
return global[k];
5 任意多次+cooldown
dp方法(大概也是别人的吧但是没有存网址T_T):
local[i] 表示第i天卖出的最佳收益
global[i] 表示第i天可以卖出也可以不卖出的最佳收益
class Solution {
public:
int maxProfit(vector& prices) {
int n = prices.size();
if(n < 2) {
return 0;
}
int local[n] = {};
int global[n] = {};
for(int i = 1; i < n; i++) {
int hold = local[i-1] + prices[i] - prices[i-1];
int newhold = 0;
if(i-3 >= 0) {
newhold = global[i-3] + max(prices[i] - prices[i-1],0);
}
local[i] = max(hold, newhold);
global[i] = max(global[i-1], local[i]);
}
return global[n-1];
}
};
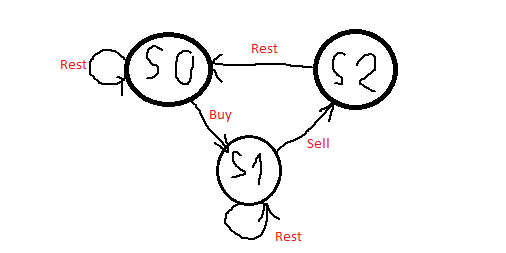
state machine method:
https://leetcode.com/discuss/72030/share-my-dp-solution-by-state-machine-thinking
图也来自上文。
s0[i] = max(s0[i - 1], s2[i - 1]); // Stay at s0, or rest from s2
s1[i] = max(s1[i - 1], s0[i - 1] - prices[i]); // Stay at s1, or buy from s0
s2[i] = s1[i - 1] + prices[i]; // Only one way from s1
初始情况:
s0[0] = 0; // At the start, you don't have any stock if you just rest
s1[0] = -prices[0]; // After buy, you should have -prices[0] profit. Be positive!
s2[0] = INT_MIN; // Lower base case
完整代码:
class Solution {
public:
int maxProfit(vector& prices){
if (prices.size() <= 1) return 0;
vector s0(prices.size(), 0);
vector s1(prices.size(), 0);
vector s2(prices.size(), 0);
s1[0] = -prices[0];
s0[0] = 0;
s2[0] = INT_MIN;
for (int i = 1; i < prices.size(); i++) {
s0[i] = max(s0[i - 1], s2[i - 1]);
s1[i] = max(s1[i - 1], s0[i - 1] - prices[i]);
s2[i] = s1[i - 1] + prices[i];
}
return max(s0[prices.size() - 1], s2[prices.size() - 1]);
}
};