oneNote的算法笔记 格式很差 请谅解
O这个是欧 不是零
只要高阶项不要低阶项.. 下面理解:
就是由等差数列转换而来
就是这里 这个就是常数操作表达式 不要低阶项 只要高阶项 并且忽略掉高阶项的系数 我们这里只需要n2 所以时间复杂度是o(n2)
书上是利用极限的思想 我们这里是更快的明白
流程1方法的 时间复杂度是big O(M*N) 需要遍历M*N次
二分查找的 时间复杂度是 log2(N)的时间复杂度
流程2方法 的时间复杂度就是O(M*logN) 注意A是有序的
流程3 注意是不在A中出现的 先不考虑排序代价
外排 就是这两个a和b a和b进行比较 当二者哪个更小的时候 移动到下一位 继续比较 当两边其中一个移动到末尾的时候 结束
就是当b<=a的情况(b才会移动,而且还要判断b=a这个不打印,b
时间复杂度: 这两个加起来
这里的O(N+M) 因为A和B都要进行移动 所以复杂度是N+M
如果0位置的数比1位置上的数大 那么就交换 下一步看1位置和2位置的数 依此类推 前一个数如果比后一个数大的话 就进行交换 这样做完一圈最大的数来到最后的位置 那么现在就排好了一个数 我们就可以减少一个数进行排序了
就是我们一开始说的那个 就是0-n-1 找一个最小的放到0位置上 然后1-N-1找一个最小的放到1的位置 这个就是选择排序
这里的i就是我们开头的位置
上面的两种排序 在工程上几乎都见不到了 只是方便我们理解时间复杂度
插入排序很有用
0-0 是可以不用排的 0-1进行排 小的放左边,然后0-2之间的数进行比较 2位置上的数 先和1位置的数比较如果小就交换 0和1 继续比较
就相当于 手上有一副已经排好的牌 需要再拿一张新的牌 挨个进行比较 插进去
swap这里其实就是这个 交换两个数
这里的情况 就要用到最好情况 最坏情况 还有平均情况 需要看具体的数据状况 我们一般用最差情况 来估计时间复杂度
对数器很重要
如果写出了一个排序 怎么来验证她对不对 还可以用在贪心策略 验证这个贪心策略对不对
需要实现一个随机样本的产生器 生成一个数组 长度和值都是随机的
再准备一个绝对正确的方法 时间复杂度高的算法容易写 我们这里验证的是时间复杂度低的算法
然后再大样本测试
参加比赛的时候或者笔试的时候 应该准备对数器模板 二叉树的 数组的 可以验证哪一个出错了
还有堆 排序等等这些都需要准备模板
1小时30分左右
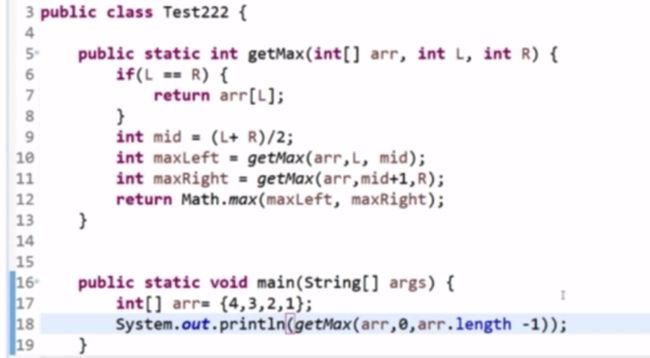
一个简单的利用递归 查找数组中的最大值
递归函数就是系统帮我们压栈 函数是如何自己调用自己的 栈里记录方法的参数和方法里面的变量还有执行到哪一步 以及相应的所有信息都会压入栈中 相当于被归档 然后再跑子过程
任何递归行为都可以改为非递归 就是从递归变成迭代了
如何分析复杂度: 这是一个高深的话题 这里我们讲一个通例
样本量为N的情况下 时间复杂度为 T代表Time
只要满足这个公式 的复杂度就是为
所以这里的复杂度是 O(N)
2:03开始
这个就用到了master公式的求解 归并排序就是先左侧部分排好序 再右侧部分排好序 然后整体利用外排的方式排好 当左右两侧排好序后 准备一个辅助数组
谁小 谁就往这个辅助数组里面填充
当整体有序了 再拷贝回原数组
代码:
面试中特别常见的题型 小和问题和逆序对问题
小和问题 可以使用归并排序 先拆分成左右 两边 分治的思想
代码讲解:2:40 这里代码的意思是 左侧部分产生的小和 + 右侧部分产生的小和 +整体产生的小和
防止溢出 如果溢出的话 算出的下标是有可能是不对的 因为L+R可能会溢出 上面的写法不安全
位运算比算术运算快很多