A
题意
给一个n,求范围[1,n]内所有数中,所有数位都相等的数的个数,如111,22,3等
思路
求出n的位数d,则数位长度为[1,n-1]的数各有9个,再考虑数位长度为n的数,从高位向低位推,设最高位数字为k,如果当前位等于k,则继续往下推。否则,若大于k,则最可取k个,若小于,则只能取k-1个。最后计算一下答案。
代码
#include
using namespace std;
int d[15];
int main()
{
int T;
cin>>T;
while(T--)
{
int n,len=0;
scanf("%d",&n);
while(n)
{
d[len++]=n%10;
n/=10;
}
int res=0,flag=0;
for(int i=len-2;i>=0;i--)
{
if(d[i]==d[len-1])
continue;
if(d[i] B
题意
给定一个序列,有奇有偶。偶数k可以通过一次操作变为k/2。所有相同的k可以用一次操作同时变为k/2。求使得整个序列全部为奇数所需要的最少操作次数。
思路
k/2等价于k>>1,所以很容易可以想到对于同一个奇数所扩展出来的偶数,只需要取最大所需操作即可,如12,6,都由3扩展而来,对12进行一次操作会得到两个6,再一次操作即可完成目标。所以方法就很明确了,扫一遍序列,记录一下当前数由那个奇数扩展而来,然后用map记录一下最大值,最后加起来就好了。
代码
#include
using namespace std;
const int MAX=2e5+5;
int odd[MAX];
mapmp;
int main()
{
int T;
cin>>T;
while(T--)
{
int n,x,len=0,res=0;
mp.clear();
scanf("%d",&n);
for(int i=0;i>=1,cur++;
if(!mp[x])
odd[len++]=x;
mp[x]=max(mp[x],cur);
}
for(int i=0;i C
题意
给一个字符串,每次操作可以去掉一个字符,求最少操作数使得整个字符串不包含任何one和two子串。
思路
很显然,除了twone这种情况可以一次操作去掉两个以外,对于每一个one,two子串都得操作一次,所以先扫一遍,去除twone这种子串的o,再扫一遍去除单独的one和two,对于单独的这种应该删除中间的字符,因为删除两边的可以会接上,如oonee这种。
代码
#include
using namespace std;
const int MAX=2e5+5;
char s[MAX];
int res[MAX];
int main()
{
int T;
cin>>T;
while(T--)
{
scanf("%s",s);
int cnt=0,len=strlen(s);
for(int i=2;i D
题意
给一堆字符串,仅由0和1组成,每个字符串不重复,然后玩玩接龙,1结尾的接1开头的,以此类推。但是这些字符串可能无法完全拼接在一起。所以给一种操作,每次操作可以翻转某一个字符串,但是必须保证所有字符串不重复。求是否可以使得所有字符串拼接在一起,可以则输出操作次数,否则输出-1。
思路
很显然字符串有4种,根据开头结尾记为01,10,00,11。00和11型可以忽略,因为可以不影响结果地接到01和10型上。所以只考虑01和10型。当且仅当两者数量差距小于等于1时可以完全拼接,所以记录一下数量,然后多出来的一半的翻转分配过去就好了。再用哈希记录一下翻转后的字符串是否出现过,若出现过,则不可翻转,往下推。再特判一下两者数量全为0的情况就可以了。3s时间挺充裕的,所以直接用STL实现。
代码
#include
using namespace std;
const int MAX=4e6+6;
vector >v01,v10;
unordered_mapmp01,mp10;
vectorout;
void init()
{
out.clear();
v01.clear();
v10.clear();
mp01.clear();
mp10.clear();
}
int main()
{
int T;
cin>>T;
while(T--)
{
int n,a=0,b=0,c=0,d=0;
string s;
init();
scanf("%d",&n);
for(int i=1; i<=n; i++)
{
cin>>s;
int len=s.size();
if(s[0]==s[len-1])
{
if(s[0]=='0')
c++;
else
d++;
continue;
}
if(s[0]=='0')
a++,v01.push_back(make_pair(i,s)),mp01[s]=1;
if(s[0]=='1')
b++,v10.push_back(make_pair(i,s)),mp10[s]=1;
}
if(a==b)
{
if(a!=0)
printf("0\n\n");
else
{
if(c==0||d==0)
printf("0\n\n");
else
printf("-1\n\n");
}
continue;
}
int ch=abs(a-b)/2,res=abs(a-b)/2;
if(a E
题意
给一个无向图,再给出两节点a,b,求有多少点对x,y满足从x到y必定经过这两个节点。
思路
理想情况是a,b直接相连,他们的连边为此无向图的割边。此时答案即为a,b各自连接的节点个数之积。可以在此情况上做一下拓展。得到如下模型。
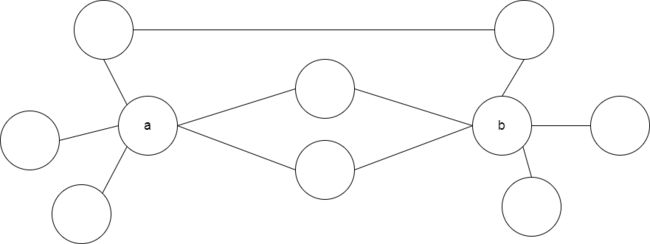
根据此模型我们可以看出,只需要计算a不经过b能到达的节点数,b不经过a能到的的节点数,再排除掉共同可达的节点数就可以变为理想模型。所以用dfs计数即可。注意一下极限情况乘积可能会溢出。
代码
#include
using namespace std;
const int MAX=2e5+5;
typedef long long ll;
vectorG[MAX];
int vis[MAX],common;
ll dfs(int x,int t,int k)
{
if(x==t)return 0;
if(vis[x]&&vis[x]!=k)
common++;
vis[x]=k;
ll ans=1;
for(int i=0; i>T;
while(T--)
{
int n,m,a,b;
scanf("%d%d%d%d",&n,&m,&a,&b);
for(int i=1; i<=n; i++)
G[i].clear(),vis[i]=0;
common=0;
while(m--)
{
int u,v;
scanf("%d%d",&u,&v)`;
G[u].push_back(v);
G[v].push_back(u);
}
ll aa=dfs(a,b,1)-1,bb=dfs(b,a,2)-1;
printf("%I64d\n",(aa-common)*(bb-common));
}
}