最近系统学习了神经网络训练中常见的gradient descent系列优化算法,现将学习笔记整理如下,主要包括:
1.深度学习与单纯的最优化有何不同
2.基础的graident descent算法
3.基于momentum的改进算法
4.基于adaptive learning rate的改进算法
5.总结1. 深度学习与单纯的优化有何不同
深度学习可以简单理解为减小(优化)损失函数的过程,这与单纯的最优化一个函数十分相似,但深度学习并不是单纯的最优化,主要区别是目标不同.深度学习的目标是模型在测试集上的performance,也就是减小泛化误差.而训练过程中我们只可以利用训练集,因此深度学习的优化目标是间接的.对于单纯的最优化而言,优化目标往往是直接的,例如,如果将优化目标定为最小化训练集上的损失函数,则深度学习在训练集上的训练过程,就可以视为单纯的最优化过程.
2. 基础的gradient descent算法
根据一次迭代(更新一次模型参数)所使用的数据量,可以分为Batch gradient descent(BGD)、 Stochastic gradient descent(SGD)和Mini-batch gradient descent(MBGD).BGD一次迭代使用整个训练集的数据,SGD一次迭代使用1个训练样本,MBGD是前两种方法的trade-off,一次使用一小批样本(如32,64,128等).其更新公式可以统一描述如下:
x += -learning_rate * dxx为模型参数,dx为x的梯度大小.三种算法的区别在于计算dx所使用的训练样本数目.
- BGD方法因为使用整个训练集计算梯度,得到的梯度是损失函数在该位置真实的梯度,所以能够保证收敛到全局最优点(凸函数)或局部最优点(非凸函数).缺点是时间和空间复杂度较高,因为BGD计算所有训练样本才能更新一次模型参数,更新依次模型参数需要花费更多的时间.同时如果利用向量化的方式实现BGD,需要缓存整个训练样本集,对于大规模训练集也难以实现.
- SGD方法利用单个样本的梯度估计整个训练接的梯度,得到的梯度具有较高的误差,因此利用该梯度更新模型参数不一定会使得损失函数减小,往往随着迭代的过程,损失函数会出现波动的现象,并且SGD最终也难以在局部最优点附近停止,而是在其周围震荡,如果随着迭代减小learning_rate,SGD也可以同BGD一样收敛到最优点.SGD虽然更新模型参数的频率更快,但是更新参数使用的梯度带有较高的噪声.
- MBGD方法是介于前面两种方法之间,每次从训练集中随机抽取一小批训练样本,用于计算梯度完成一次模型参数更新,相比于BGD,MBGD方法迭代频率更高,训练速度更快.相比于SGD,迭代使用的梯度更加准确,训练过程更加稳健,利用向量化实现过程也可以实现较快的运算.
上述三种方法中,Mini-batch gradient descent是目前最常采用的训练方式,一般提到的SGD也代指的是MBGD方法,Mini-batch的训练方式也是后续momentum gd等改进方法的训练模式.
基础的gradient descent方法具有一些共有的弱点,主要包括:
- learning_rate选择的问题,基础的gd方法需要人工设置合适的超参数learning_rate,学习率过小会使得训练非常缓慢,学习率过大会导致训练难以收敛甚至发散.
- learning_rate对于每个维度的特征都是相同的,但是对于不同出现频率的特征或者曲率相差很大的特征(损失函数的Hessian矩阵病态,特征值大小相差很大),我们往往希望它们具有不同的学习率.
- 无法逃逸大量存在的鞍点的问题.(大型神经网络中收敛到一个不错的局部最优点也是可以接受的,真正带来麻烦的是大量存在的鞍点,而鞍点周围往往存在梯度很小的平原,该问题会在总结部分进行展开论述).
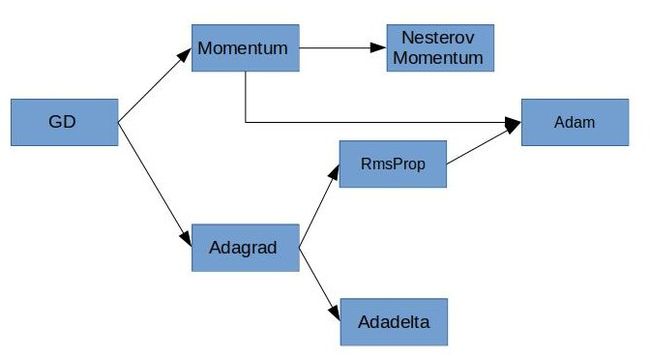
针对基础的gd存在的上述挑战,大牛们对gd算法进行了魔改,主要有两条线路,改进发展如下图,下面两节分别介绍两类改进方法.
3. 基于momentum的改进算法
3.1 指数加权滑动平均方法
两类改进基础gradient descent的方法都使用了指数加权滑动平均的方法,相比于算数平均运算,该方法时间复杂度和空间复杂度都有较大优势.定义如下:
\[v_t = \beta v_{t-1}+(1-\beta)\theta_t\]
其中,\(\theta_t\)为指数加权平均的数据,\(v_t\)为指数加权平均的结果,\(\beta\)为指数加权参数,一般设置\(v_0=0\).
- \(\frac{1}{1-\beta}\)近似为指数加权平均的数据个数,例如,\(\beta=0.9\),则\(v_{20}\)则代表这\(\theta_{20}\)到\(\theta_{11}\)的指数加权平均结果,在\(\theta_{11}\)之前的数据也对结果有影响,但影响十分有限,可以忽略.
- 上面迭代求解的过程,在运算初期会有明显的偏差,纠正方法是令\(v_t = \frac{v_t}{1-\beta^t}\)
3.2 momentum算法
momentum算法的更新公式如下:
v = mu*v - learning_rate * dx
x += v其中,v是指数加权滑动平均累加量(该公式与2.2节计算公式形式不同,但指数加权滑动平均的思想一致),mu是momentum引入的超参数(一般设置为0.9).
momentum算法可以借用物理概念很好的理解,想象一个小球从山顶滚落,mu*v这一项相等于速度项(忽略其符号),后面一项相当于加速度项,小球在滚落过程中,不仅受到当前时刻的加速度影响,而且收到积累起来的速度影响(momentum相较于基础gd多出来的部分),类似于加了惯性作用,而mu参数是一个decay参数,类似与摩擦力的作用,随着迭代进行,时间久远的累加值起到的作用将越来越微弱.
当特征间曲率差异大时,基础的GD方法会产生zigzag现象,会在曲率大的方向上有较大的震荡,而曲率小的方向上前进较慢,momentum算法可以有效抑制这种现象.训练对比图像如下所示(图片来自"花书")
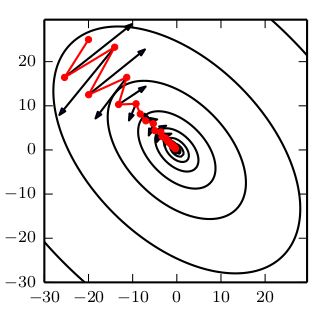
图中椭圆为损失函数等高线,显然45°方向上特征具有更大的曲率.红色实线为momentum训练过程,黑丝箭头表示基础GD在该位置将要迭代的位置.比较可见momentum有效减小了训练过程中曲率较大方向上的震荡,增加了曲率较小方向上的迭代步长.这是因为在指数加权滑动平均的过程中,曲率较大方向上的梯度由于正负交替出现,进行了抵消,而曲率较小方向上的梯度符号一致,累加的过程中增大了梯度,等效于增加了迭代步长.
momentum方法使得训练过程带有惯性,好的方面是可能便于训练逃逸损失函数的鞍点或者平坦区域,不好的方面是在到达最低点时,由于带有惯性不能立刻停止,会发生overshoot最低点的现象.
3.3 Nesterov momentum算法
前面提到Momentum算法在最低点会发生overshoot现象,能不能在快到底最低点前减小梯度,就能减弱该现象,Nesterov momentum正式基于这个考虑改进momentum算法的.其更新公式如下:
\[v_{t} = \mu v_{t-1} - \alpha \nabla(\theta_{t-1}+\mu v_{t-1})\]
\[\theta_t = \theta_{t-1} + v_t\]
比较momentum算法可见,唯一的区别是计算梯度部分,Nesterov相较于momentum计算的是参数\(\theta_{t-1}\)更新\(\mu v_{t-1}\)之后的梯度.Nesterov的思想是既然我们已经知道了参数\(\theta_t\)要更新\(\mu v_{t-1}\)这一部分,为什么不先用\(\mu v_{t-1}\)更新参数,然后在计算梯度呢,这样用\(\theta_{t-1}+\mu v_{t-1}\)近似模拟了\(\theta_t\),起到了前瞻梯度的效果.至于Nesterov为什么要比momentum效果好,而已这样理解,当前瞻到的梯度比当前梯度大时,这一步更新的梯度会更大,反之,当前瞻到的梯度比当前梯度小时,这一步更新的梯度会更小.
例如小球从山顶向山底滚落,开始阶段,当山坡的斜率越来越大时,由于前瞻到的梯度比当前梯度要大,所以更新步幅越来越大,可以加快训练.当小球接近山底时,山坡梯度越来越小,则更新歩幅会提前缩小,可以见减小overshoot现象.
4. 基于adaptive learning rate的改进算法
前面介绍了基于momentum的改进算法,这一类改进算法能够加速gd的收敛过程,并且对于不同曲率的特征起到了很好的平衡效果.本节主要介绍给予自适应学习速率的改进方法,这一类方法能够自适应地赋予不同频率(泛指的)的特征以不同的学习速率.
4.1 Adagrad算法
Adagrad算法是这一类改进算法的鼻祖,更新公式如下:
cache += dx**2
x += -learning_rate * dx / np.sqrt(cache + 1e-7) Adagrad算法对各个参数的梯度平方进行了累加,并将当前的梯度用累加值进行了加权,可以发现某个参数的梯度较大,则其累加和比较大,则最终更新参数时其权重越低,也就是学习率越小.而某个参数的梯度较小,则其累加和也比较小,则其学习率衰减的比较慢.
为什么说Adagrad对不同出现频率的特征具有赋予不同的学习率,个人理解是,不同维度的特征可以理解为不同参数的梯度(有很大的欠妥,但根据求导法则,特征往往是模型参数梯度的重要影响因素,例如\(z = \theta_1x1+\theta_2x2\),参数\(\theta_1,\theta_2\)的梯度分别为x1和x2),则某些维度的特征出现频率很低,则其累加值会比较小,则其学习率就相对更大.
Adagrad算法具有非常明显的弱点,那就是梯度平方的累加会越大越大,各个参数的学习率会被衰减的越来越小,导致后期训练越来越慢,可能难以到达最优点.后面的方法针对这一点进行了改进.
4.2 RMSProp算法
RMSProp算法不是公开发表论文中的算法,而是大牛Geoff Hinton在一次授课中提出的算法,主要思想是将指数加权滑动平均思想引入了Adagrad算法,更新公式如下:
cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += -learning_rate * dx / np.sqrt(cache + 1e-7) 指数加权滑动平均思想的引入,使得cache发生指数衰减,缓解了Adagrad后期学习率衰减过小的问题.decay_rate是RMSProp算法引入的超参数,一般设置为0.9.
4.3 Adadelta算法
Adadelta算法相较于RMSProp算法,用另外一个指数加权平均替换掉了全局learning_rate,其更新公式如下:
cache = decay_rate1 * cache + (1 - decay_rate1) * dx**2
dx^ = dx * np.sqrt(delta + 1e-7) / np.sqrt(cache + 1e-7)
x += - dx^
delta = decay_rate2 * delta + (1-decay_rate2) * dx^ ** 2Adadelta缓存了模型参数更新平方的指数加权平均,作为自适应的全局learning_rate,因此我们完全不需要人为设置一个全局学习率了.
4.4 Adam算法
Adam算法结合了momentum和RMSProp两种算法,并添加了指数加权滑动平均的偏差矫正,其更新公式如下:
m = beta1 * m + (1 - beta1) * dx
v = beta2 * v + (1 - beta2) * dx**2
m /= 1 - beta1**t
v /= 1 - beta2**t
x += -learning_rate * m / (np.sqrt(v) + 1e-7)其中参数t是迭代次数,beta1,beta2是Adam算法引入的超参数,beta1,beta2的默认值为0.9和0.999.
5.总结
本篇笔记总结了深度学习中常见的优化算法,主要包括基础的Gradient descend算法和两类改进算法,其中Adam算法是两类改进算法的集大成者,兼具momentum系列算法和adaptive learning rate算法的优点,是受到普遍推荐的算法.实际应用中,据说基础的gd方法往往能够达到更低的loss,所以有前段使用Adam算法加速训练,后期采用基础gd收敛到更低点的做法.
上述内容之外,还有三个额外的内容.
5.1 关于优化方法的可视化
本部分的动图来源于Sebastian Ruder的综述文章,可以形象的对比各个不同算法的性能.图中NAG算法代指Nesterov momemtum算法.
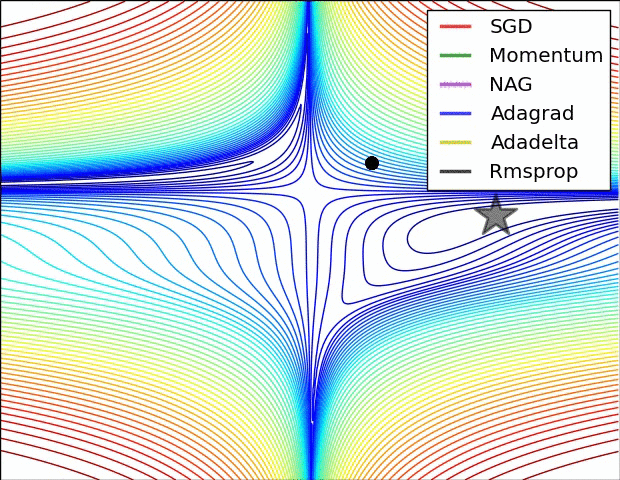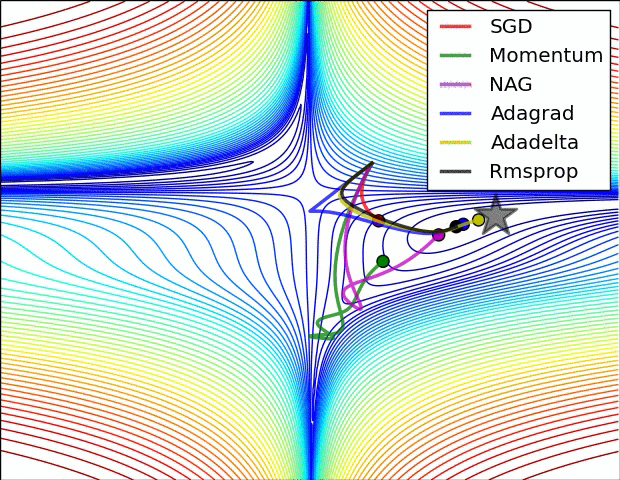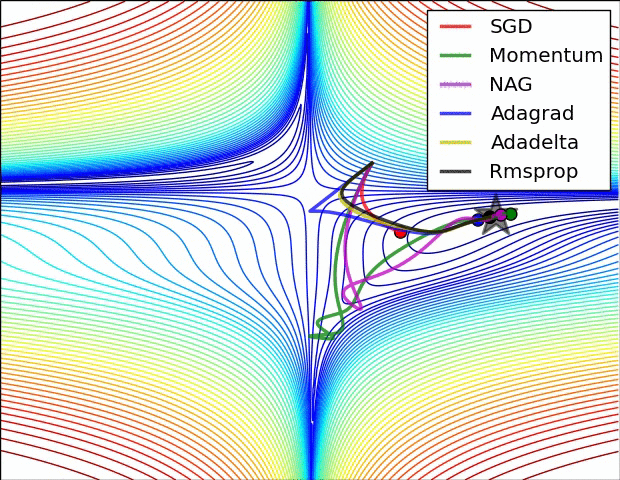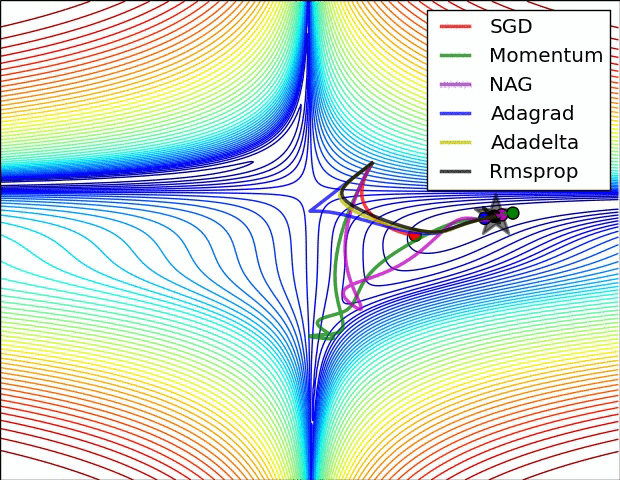
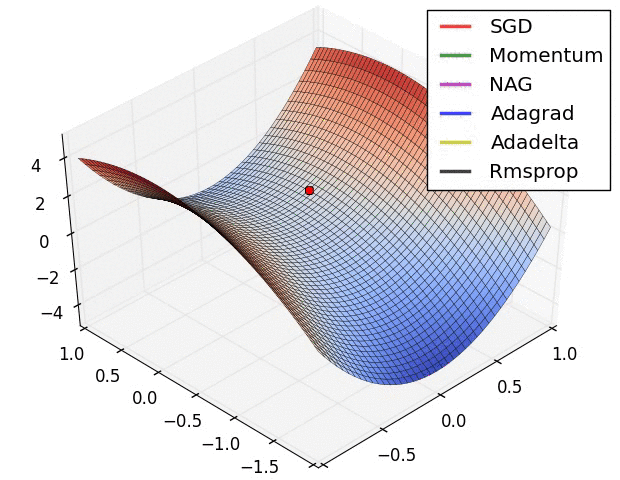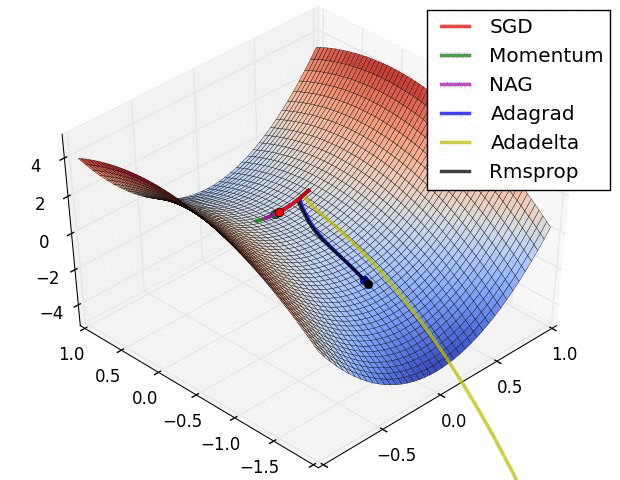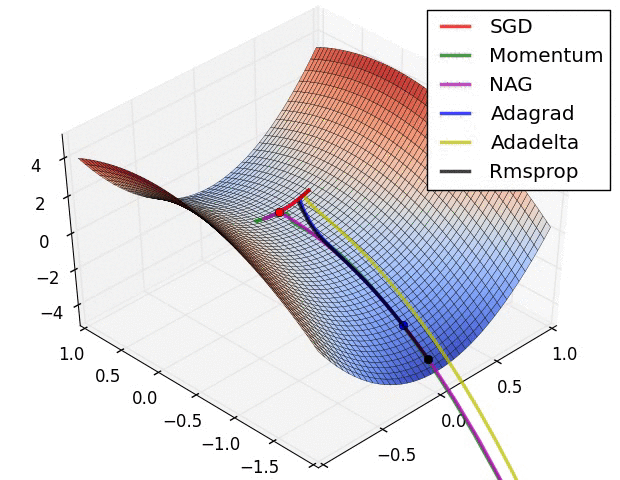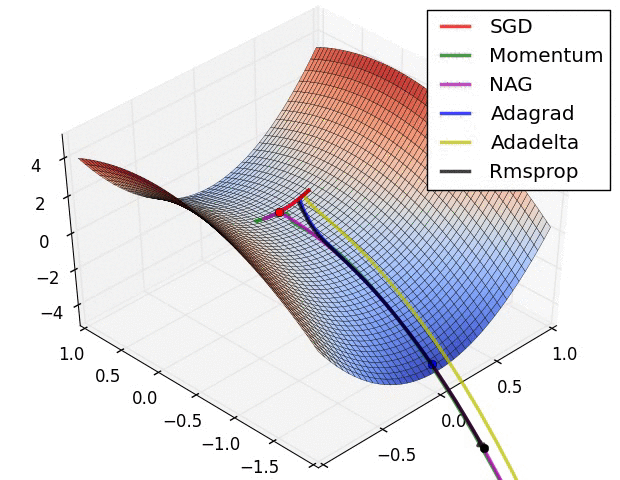
5.2 关于深度学习中局部最优和鞍点的问题
在之前神经网络的优化过程中,人们非常担心陷入局部最优,而无法找到全局最优的问题,而在深度神经网络中,我们更为关心的是优化算法逃逸鞍点的问题,为什么会这样呢?主要是基于两点考虑(理解自花书):
- 对于深度神经网络而言,鞍点的数量远大于局部最优点的数量(遇到鞍点的额概率高得多),这是因为局部最优点要求损失函数特征值全部大于0(正定的),也就是所有特征的曲率都是大于0的,这对于高维空间而言出现的概率远低于鞍点(鞍点要求曲率有正有负).类似与抛出大量的硬币,要求硬币都是同一面朝上的概率要低很多.
- 对于深度神经网络而言,找到一个局部最优点是可以接受的,因为大型神经网络中的局部最优点也具有很小的损失函数.
5.3 关于选择learning_rate的问题
learning_rate选择的问题其实也属于超参数训练的范畴,实践中是需要根据不同的任务和训练样本进行调试的,对于基础的gd方法,基于momentum的改进方法,往往需要decay learning_rate,使得训练初期速度较快,而后期能够收敛到最低点.对于adaptive learning rate算法,理论上只需要设置一个全局learning_rate就可以,算法本身带有学习率调整策略.
参考内容:
1.Deep Learning(花书,Ian Goodfellow and Yoshua Bengio and Aaron Courville)
2.An overview of gradient descent optimizationalgorithms
3.CS231n Convolutional Neural Networks for Visual Recognition