Codeforces Round 604 Div2

A

题意

给一个字符串，由a,b,c字母和?组成。 ?可以填成a,b,c中的一个。求是否存在一种填法使得：字符串不存在任何相邻位置的字母相同。存在则输出填充后的字符串，不存在输出-1。

思路

对于任何一个位置，只有两个邻居，但是有三种填法，所以说每个问号必定可以合法填充。按规则填完后检测一下就好了。

代码

#include

using namespace std;
const int MAX=1e5+5;

char s[MAX];
bool vis[3];
int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        scanf("%s",s);
        int len=strlen(s);
        for(int i=1; i1?s[1]:'a')-'a'+1)%3+'a';
        if(s[len-1]=='?')
            s[len-1]=((len>1?s[len-2]:'a')-'a'+1)%3+'a';
        bool flag=1;
        for(int i=1;i

B

题意

给定1-n的一个排列，求对于1-n的每个m，是否存在一个区间使得1-m所有数均在这个区间中。

思路

记录一下数i的位置，记为pos[i]。然后递推处理，记max为1-i中出现的最大位置，min为最小位置。则可以保证前i个数一定出现在[min,max]之间。若此时max-min+1==i即区间长度为i则说明前i个数均在此区间内，即长为i的区间存在。

代码

#include

using namespace std;
const int MAX=2e5+5;

int pos[MAX];

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        int n,x;
        scanf("%d",&n);
        for(int i=1; i<=n; i++)
            scanf("%d",&x),pos[x]=i;
        printf("1");
        int minn=pos[1],maxx=pos[1];
        for(int i=2; i<=n; i++)
        {
            minn=min(minn,pos[i]);
            maxx=max(maxx,pos[i]);
            if(maxx-minn+1==i)
                printf("1");
            else
                printf("0");
        }
        printf("\n");
    }
}

C

题意

比赛发牌子，给出n个队伍的过题数，发g个金牌，s个银牌，b个铜牌，使得g,s,b满足以下要求：

• g，s，b > 0
• g < s且g < b
• 金牌队伍过题数必须严格大于银牌队伍
• 银牌队伍过题数必须严格大于铜牌队伍
• 铜牌队伍过题数必须严格大于无牌队伍
• 总奖牌数小于队伍数量一般（向下取整），即g+s+b < n/2

思路

贪心依次推，在满足1，3条件的前提下g尽可能少，在满足1，2，4条件的前提下s尽可能少，b取满足1，5条件的剩余结果，若都能满足则有解，否则无解。

代码

#include

using namespace std;
const int MAX=4e5+5;

int a[MAX];

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        int n;
        scanf("%d",&n);
        for(int i=0;i0)ed--;
        while(p=s||g>=b)
            g=s=b=0;
        printf("%d %d %d\n",g,s,b);
    }
}

D

题意

有0，1，2，3这四种数，分别有a,b,c,d个，求如何排列使得序列任意相邻的两个数差距，即abs(a[i]-a[i+1])，不超过1。

思路

很显然0必须和1相邻，3必须和2相邻，所以至少需要a个1，d个2,所以b-=a,c-=d，然后看此时的c，d之差距是否不超过1，若是则有解，输出，否则无解。 再特判一下0，1数量全为0或者2，3数量全为0的情况即可。

代码

#include

using namespace std;

int main()
{
    int a,b,c,d;
    scanf("%d%d%d%d",&a,&b,&c,&d);
    int bb=b-a;
    int cc=c-d;
    if(a==b&&a==0&&d-c==1)
    {
        printf("YES\n3 ");
        for(int i=0;i1)
    {
        printf("NO\n");
        return 0;
    }
    printf("YES\n");
    if(bb==cc)
    {
        for(int i=0;i

E

题意

一个人有n个魔镜，第i个魔镜有pi的概率说这个人好看。现在从第一个魔镜开始问起，每天问一个，若魔镜说好看则第二天继续问下一个，若说不好看则第二天从第一个魔镜重新开始问起。若第n个魔镜说好看则这个人会变开心。求让他变开心所需要的天数的期望，输出对998244353取模。

思路

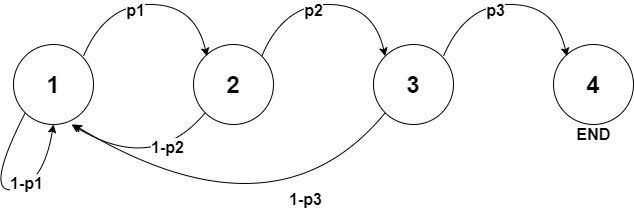
求期望，马尔可夫链，由出边连接节点向本节点转移。可得如下模型。

设dp[i]表示由第i个魔镜开始询问到达最终状态的期望天数。
最后一个魔镜也需要询问，所以设最终状态为dp[n+1]=0。即由最终状态转移到最终状态期望天数为0。
最终答案即为dp[1]由此模型推导得出
\[ dp[1]=dp[2]*p+dp[1]*(1-p_1)+1\\ \Rightarrow dp[1]=dp[2]+\frac 1p_1 \qquad(1)\\ dp[2]=dp[3]*p_2+dp[1]*(1-p_2)+1\\ 代入(1)\Rightarrow dp[1]=dp[3]+\frac 1p_2+\frac 1{p_1p_2} \]
可得规律
\[ dp[1]=dp[n+1]+\frac 1p_n+\frac1{p_np_{n-1}}+\cdots+\frac 1{p_n \cdots p_1}\\ \Downarrow\\ dp[1]=\frac {p_{n-1}\cdots p_1+p_{n-2}\cdots p_1+\cdots+p_1+1}{p_1\cdots p_n} \]
计算出此式即可。有除法取模，所以要求逆元。模数为质数，用费马小定理。乘一个1ll提升字节数防止溢出。

代码

#include

using namespace std;
const int mod=998244353;

int qpow(int a,int k)
{
    int res=1;
    for(;k;k>>=1)
    {
        if(k&1)
            res=1ll*res*a%mod;
        a=1ll*a*a%mod;
    }
    return res%mod;
}

int inv(int x){return qpow(x,mod-2);}

int main()
{
    int a=0,b=1,n,inv100=inv(100);
    scanf("%d",&n);
    for(int i=0;i