最近在看名人介绍,突然看到了一篇文章介绍伯努利家族,觉得他们家族那两代人特别有意思,就想写出来,让大家都知道。
瑞士的伯努利家族是世界颇负盛名的科学世家,出了好几个有名的科学家,驰骋影响学界上百年。学物理的人都知道流体力学中有一个著名的伯努利定律,说的是有关不可压缩流体沿着流线的移动行为,由丹尼尔•伯努利(DanielBernoulli,1700-1782)提出。丹尼尔的父亲和伯父则都是他们那个时代著名的数学家。
有意思的是,伯努利家族这几个科学家之间,相处得并不和谐。互相在科学成就上争名夺利、纠纷不断。尤为后人留下笑柄的是丹尼尔的父亲:约翰•伯努利。
恩怨情仇之兄弟反目
约翰•伯努利(JohannBernoulli,1667-1748)和他的哥哥雅各布•伯努利(JakobI. Bernoulli,1654-1705)都为微积分的发展作了杰出贡献。约翰进入巴塞尔大学时,比他大13岁的雅各布已经是数学系教授,因此,约翰向大哥学习数学。两人既是兄弟手足,又是导师和学生的关系。
约翰天资聪明,拜大哥为师的两年之后,数学能力就达到了与哥哥能一比高低的水平。没想到智力水平的高低并不等价于人品和修养的高低,约翰不服雅各布,雅各布却仍然将弟弟看成一个学生,两兄弟之间逐渐形成了一种不十分友好的竞争状态。约翰十分妒忌雅各布在巴塞尔大学的崇高地位,于是,无论在私底下,还是在大庭广众中,两人经常互相较劲。
不过,世人可以不齿于他们互相嫉妒诋毁的人格,却不能否认他们这种竞争较劲的状态,还算有利于学术。从下面的几个例子,便是对以上说法的佐证。
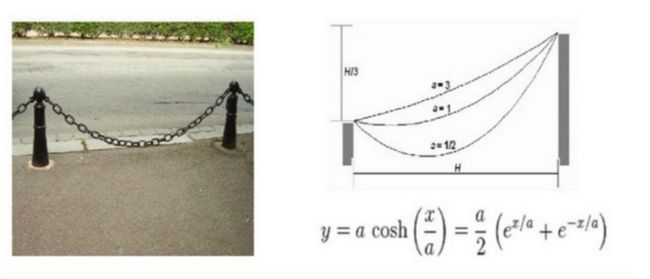
那个时代的欧洲数学家,有一股互相出难题来挑战学术界的风气。1691年,哥哥雅各布建议数学家们研究悬链线(Catenary)问题,也就是两端固定的绳子(或链条)由于重力而自由下垂形成的曲线到底是个什么形状的问题。这个问题现在看起来简单,但在微积分和牛顿力学尚未建立以及刚刚建立的年代,却是不容易解决的。
伽利略在1638年就曾经错误地猜测悬链线是抛物线,后来(1646年),17岁的少年惠更斯证明了悬链线不是抛物线。但不是抛物线,又是什么线呢?它的方程是怎么样的?当时谁也不知道答案。悬而未决的悬链线问题在等待着微积分的到来。
雅各布收到了好几个答案,其中包括萊布尼茨、惠更斯以及他的弟弟约翰•伯努利。他们成功地用微积分解决了这个问题,证明了悬链线是如上图中所示的公式所描述的双曲余弦函数。
因为这个问题的成功,骄傲自负的约翰得意非凡,认为这是他在兄弟之争中的辉煌胜利,并更加瞧不起这个他认为“愚笨”的哥哥。约翰在多年后写给朋友的一封信中,还津津有味地描述了当时掩饰不住的“赢了哥哥”的狂喜心态。
其实,雅各布的数学成就并不逊色于弟弟,他活得没有弟弟长,50岁就去世了。约翰活到了80岁。雅各布短短的学术生涯中,对微积分及概率论作出很多贡献,其中最为众人所知的是“大数定律”。此外,数学中有许多以伯努利命名的术语,其中十几个都是雅各布的功劳。
1696年,約翰也对欧洲数学家提出了一个挑战难题,那就是著名的最速降落轨道(Brachistochrone curve)问题,也就是:什么形状的滑梯,才能使得滑动者到达地面的时间最短呢?这实际上是一个著名的数学问题,微积分方法的出现促成了它的解决,并由此而开拓了一门与物理学紧密联系的新的数学分支:变分法和泛函分析。
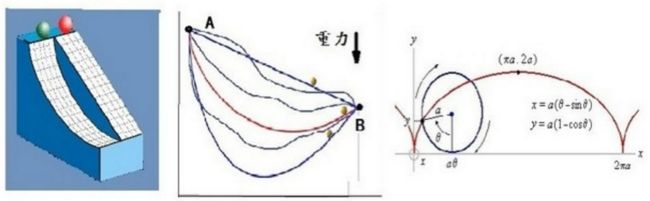
假设A和B是地面上高低不同(A不低于B)左右有别的两个点,如下图左图所示。一个没有初始速度的小球,在无摩擦力只有重力的作用下从A点滑到B点。从A到B的轨道可以有很多很多,各自有不同的形状和长短,见下图中间一图。问题是:这其中的哪一条轨道,将使得小球从A到B的时间最短?
如果问的是距离最短,大家在直观上都知道答案是直线,但现在是要你求出所花时间最短的曲线,直观就不太顶用了。
有人估计约翰自己当时已经得出了这个问题的答案,而提出这个问题的目的之一是挑战牛顿,其二则是奚落自己的哥哥。奚落雅各布是约翰的嫉妒心所致,为啥又要挑战牛顿呢?原因是在牛顿与萊布尼茨对微积分发明权的争夺战上,约翰是始终坚定地站在自己的老师萊布尼茨一边的。
约翰原来规定答案必须在1697年1月1日之前寄出,后来在萊布尼茨的建议下,将期限延长至复活节。期限延长后,为了确保牛顿得知此事,约翰亲自将问题单独寄了一份给他。牛顿毕竟是大师,当时已经年过半百,正在繁忙于他的改铸新币的工作,自己也承认脑瓜子已经大不如年轻时机敏。但无论如何,据说牛顿在下午4点钟收到邮件后,仅仅用了一个晚上便解决了这个问题,并且立即匿名寄给了约翰。
这使约翰大为失望,因为他自己解决这个问题花费了两个星期的时间。虽然牛顿未署真名,约翰仍然猜出了是他,并且也不得不佩服地说:“我从利爪认出了雄狮!”(Irecognize the lion by his paw)。
复活节时,约翰共收到五份答案:除了约翰自己和牛顿的之外,还有莱布尼兹、法国的洛必达侯爵、以及他的哥哥雅各布。
尽管牛顿的才能使约翰沮丧,他仍然得意地认为自己的方法是所有答案中最简洁漂亮的,而认为他哥哥雅各布的方法最笨最差。牛顿等其余三人用的是微积分方法,在此不表。伯努利弟兄方法的差别何在呢? 约翰的答案简洁漂亮,是因为他借用了光学中费马的光程(或时间)最短原理。
法国数学家费马(Fermat,Pierrede,1601-1665)是个很奇怪的学者,他是法院的法律顾问,算是个业余数学家。他的特点是不怎么发表著作,经常是只在书的边缘处写下一些草率的注记,或者是偶然地将他的发现写信告诉他的朋友。现在看来,即使是这种草率注记中的三言两语,已经使世人震撼忙碌不已,要是费马正儿八经地专门研究数学,那还了得?
例如,1637年,费马在阅读《算术》一书时,曾写下注记:“将一个立方数分成两个立方数之和,或一个四次幂分成两个四次幂之和,或者一般地将一个高于二次的幂分成两个同次幂之和,这是不可能的。关于此,我确信已发现了一种美妙的证法,可惜这里空白的地方太小,写不下……”。就是这一段短短的注记,后来被称之为“费马大定理”的猜想,就困惑了数学家们整整358年!
费马研究光学时发现,光线总是按照时间最小的路线传播。这个原理,是几何光学的基础,可以从后来的惠更斯原理推导出来。事实上,费马原理现代版的更准确表述应该是:光线总是按照时间最小、或最大、或平稳点的路线传播。换言之,光线传播的经典路径是变分为0的路径。所以事实上,有关光线传播的费马原理应该算是变分法的最早例子,但在当时,人们尚未认识到这点,也没有进行详细的理论研究。
约翰·伯努利毕竟脑瓜子灵活,将费马原理信手拈来,把小球在重力场中的运动类比于光线在介质中的传播,导出了最速落径问题中那条费时最短的路径所满足的微分方程。这个微分方程的解,实际上就是同时代的惠更斯曾经研究过的“摆线”(沿直线滚动的圆的边界上一点的轨迹)。或者说,最速落径就是倒过来看的摆线,见图2中的右图。
约翰很得意地将最速落径问题中的物体类比于光线,貌似轻而易举地解决了问题,也得到了正确的答案(图3a)。用现代物理学对光的理解来审查约翰的解法,光和物体的确可以类比。但在当时,约翰的方法恐怕只能算是一种投机取巧,因为他完全没有证据来说明这种做法的正确性。
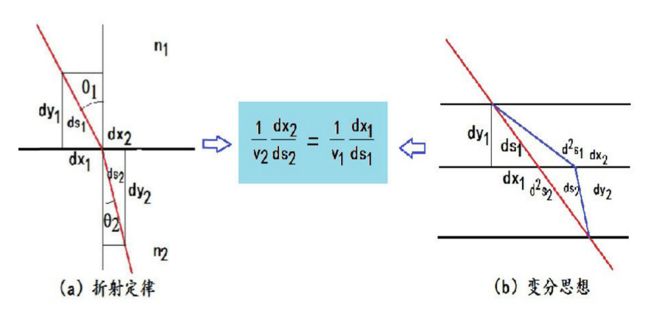
雅各布·伯努利的方法虽然被约翰看不上,认为太繁复,但却在繁复的推导中闪烁出新的变分思想的光辉。雅各布没有使用像现成的费马原理这类的东西,而是从重力运动下小球遵循的物理和几何规律来仔细推敲这个问题。他首先假设小球是沿着一条时间最短的路线下滑的,然后考虑:如果在某个时刻,小球的路线稍微偏离了这条时间最短的路线,走了别的什么路径的话,会发生什么情况呢(图3b)?
大家可以注意到,上述雅各布的做法已经是一种变分的思想,因为他是在考虑所有微小偏离路径中使得时间最小的那个偏离。然后,雅各布用二阶导数的方法证明了,在这种情形下,为了使小球继续走时间最短的路,它的路线的微分偏离量,dx和dy,应该满足的方程,就正好是摆线所满足的微分方程。
从图3中可粗略看出,约翰简单地使用费马折射定律,雅各布用考虑二阶导数的“繁琐”方法,最后都导致了同样的公式,即图3a和图3b中间的方程,解决了最速落径问题。
伯努利兄弟的你争我斗推动了变分法和泛函分析的发展。没过几年,哥哥雅各布就去世了。看来,约翰是过不了没有竞争对手的日子,他继而又把对雅各布的嫉妒心转移到了自己的天才儿子丹尼尔•伯努利的身上。
恩怨情仇之父子闹翻
丹尼尔•伯努利是约翰次子。他幼时对数学有特别的爱好。他13岁入大学学习哲学与逻辑,后来想进修数学,但他的父亲劝他说数学挣不到钱,建议他经商。不过丹尼尔的脾气很执着,后来父亲不得不让步,也像其父一样先习医,1721年获巴塞尔大学医学博士学位,但在其家族的熏陶感染下,不久便转向数学,在父兄指导下从事数学研究,并且成为这个家族中成就最大者。
1724年,他赴意大利威尼斯,其间在哥特巴赫协助下,发表《数学练习》。书的第二部分是关于流体力学的,说明从那时起他已经对流体力学产生了浓厚的兴趣。这本书立即引起学术界关注,并被邀请到俄国圣彼得堡科学院工作。同年,他还用变量分离法解决了微分方程中的“里卡蒂”方程的求解问题。第二年,25岁的丹尼尔受聘为圣彼得堡科学院数学教授,并被选为该院名誉院士。
1734年,他返回巴塞尔,教授解剖学和植物学和自然哲学.丹尼尔的贡献集中在微分方程、概率和数学物理,被誉之为数学物理方程的开拓者和奠基人。他曾10次获得法国科学院颁发的奖金,能与之相媲美的只有大数学家欧拉。丹尼尔于1747年当选为柏林科学院院士,1748年当选巴黎科学院院士,1750年当选英国皇家学会会员.他一生获得多项荣誉称号。
1734年丹尼尔回到巴塞尔之后,父子两个闹翻了。起因是,那一年丹尼尔提供了一篇关于天文学的论文去应征巴黎科学院的大奖,不巧的是他的父亲约翰也提交了应征那次大奖的论文,结果是两个人都获奖来分享那次大奖。这件事激怒了约翰,认为是儿子预先设计了一个圈套要与他平起平坐。事后丹尼尔回到他父亲的家时被拒之门外。后来一直到死,约翰也没有谅解他的儿子。这件事有可能影响后来丹尼尔没有在数学上的学术进取,再也没有他在彼得堡时对严格数学的那种激情。他说过:“如果地球上没有数学家,真实的物理也许会更好。”
如果说,在父子反目之后,丹尼尔有意回避他父亲约翰的研究领域,对数学的热情降低了许多。而相反约翰却有意去进入丹尼尔所熟悉的流体力学领域。
在大约1739年或稍后,约翰出版了一本《水力学》(hydraulics),不过注明的出版时间有意放在丹尼尔的《流体动力学》出版日期1738年之前的1732年。他这样做的目的是要人相信似乎丹尼尔的书是抄袭他的书而来的。后人评论约翰的书是一本典型的抄袭之作。
在约翰的书中,他是想尽量从牛顿的原理直接进行推演,以说明他的独立著作,不过书中有相当多的部分是取自丹尼尔书的内容。大部分结果也并没有超出丹尼尔的书。
约翰虽然在家族争斗中很牛逼,但是也还是有被人坑的时候。
恩怨情仇之发明之争
约翰与另一位数学家洛必达之间也有一段纷争,因为众所周知的“洛必达法则”,实际上是约翰·伯努利发现的。这是怎么回事呢?
原来,洛必达是一个贵族,业余时间喜欢搞一些数学,几乎到了上瘾的地步。甚至不惜花重金聘请当时的大数学家伯努利兄弟给他长期辅导。
可惜他的才气远远不如他的财气。虽然十分用功,但他在数学上仍然没有什么建树。贝努利兄弟当时正与莱布尼兹这样的大数学家交流合作,所以总有最新成果教给洛必达。这些最新成果严重地打击了他的自信心。一些他自己感到很得意,废寝忘食搞出来的结果,与伯努利兄弟教给他的最新结果比起来只能算是一些简单练习题,没有丝毫创意。
另一方面,这些新结果又更激起了他对数学的着迷。他继续请伯努利兄弟给他辅导。甚至当他们离开巴黎回到瑞士以后,他还继续通过通信方式请他们辅导。
如此持续了一段时间,他的“练习题”中仍没有什么可以发表的东西。他内心深处越来越丧气,却又不甘心。心想,我对数学如此热心,一定要想办法在数学上留下一点东西让人记住我的名字。
终于有一天,他给伯努利兄弟之一的约翰写了一封信,信中说: 很清楚,我们互相都有对方所需要的东西。我能在财力上帮助你,你能在的才智上帮助我。因此我提议我们做如下交易:我今年给你三百个里弗尔(注:一里弗尔相当于一磅银子)。并且外加两百个里弗尔作为以前你给我寄的资料的报答。这个数量以后还会增加。
作为回报,我要求你从现在起定期抽出时间来研究一些固定问题,并把一切新发现告诉我。并且,这些结果不能告诉任何别的人,更不能寄给别人或发表……
约翰收到这封信开始感到很吃惊。但这三百里弗尔确实很吸引人。他当时刚结婚,正是需要用钱的时候。而且帮助洛必达,还可以增加打入上流社会的机会。约翰想,洛必达最多不过就是拿这些结果到他的朋友那里去显示一下,没什么大不了的。算盘打下来,这笔交易还是比较化算的。于是,他定期给罗毕塔寄去一些研究结果。
洛必达都细心地研究它们,并把它们整理起来。一年后,洛必达出了一本书,题目叫《无穷小量分析》(就是现在的微积分)。其中除了他的“练习题”外,大多数重要结果都是从约翰寄来的那些资料中整理出来的。他还用了一些莱布尼兹的结果。他很聪明地在前言中写到:我书中的许多结果都得益于约翰·伯努利和莱布尼兹,如果他们要来认领这本书里的任何一个结果,我都悉听尊便。
伯努利拿了人家的钱当然不好意思再出来认领这些定理。这书中就包括了大家熟知的定理洛必达法则。伯努利眼睁睁看着自已的结果被别人用却因与人有约在先而说不出来。洛必达花钱买了个青史留名,这比后来的人花钱到某某大学买个学位划算多了。
当然伯努利不愿就此罢了。洛必达死后他就把那封信拿了出来,企图重认那越来越重要的洛必达法则。现在大多数人都承认这个定理是他先证明的了。可是人们心中先入为主的定理名字恐怕是再也变不回来了。
小结
听完这个故事,下次见到各种伯努利定理,就倍感熟悉了。
参考资料:
- 《数理同源》-3-哪条路径最快?
- 伯努利父子的恩怨
- 洛必达法则是约翰·伯努利的成果!