不下降序列问题
设由n个数组成的数列,即为:a[1]、a[2],...、a[n],若存在i1 3,18,23,24 是一个长度为4的不下降序列
> 3,7,10,12,16,24 是一个长度为6的不下降序列
问:
如何求最长不下降序列?
如何求左右不下降序列?
如何求指定长度不下降序列? 关键点: 相对位置不变; 不下降。
问题建模
使用数列中的元素和元素间的关系建立图模型[重要]
- 图中顶点的附加数据为对应的数列元素值
图中的边按照如下方式建立
当数列中的某个元素与后序元素存在不下降关系时
- 从该元素对应的顶点到后继元素对应的顶点存在一条有向边
- 边的权值固定为 1
建模示例
1, 3, 4, 2, 5
SharedPointer> create_graph(int *a, int len)
{
ListGraph *ret = new ListGraph(len);
if (ret != nullptr)
{
for (int i=0; isetVertex(i, a[i]);
}
for (int i=0; i 保证相对位置不变 !!
{
if (a[i] <= a[j]) // 保证有序不下降
{
ret->setEdge(i, j, 1);
}
}
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create graph ...");
}
return ret;
} 求最多顶点路径
以每个顶点作为起始顶点寻找局部最多顶点路径
- v
0→p0, v1→p1, ......, vn-1→pn-1寻找全局最多顶点的路径
- p
m= max { p0, p1, ......, pn-1}
局部最多顶点数路径的求解思路
- 获取当前顶点 v 的邻接顶点 {aj
0, aj1, ......}- 以各邻接顶点为起始顶点求解最多顶点路径 {p
aj0, paj1, ......}- p
v= max {paj0, paj1, ......} + 1
原材料
Array
count;
- count[i] 表示以 i 起始的最多顶点路径上的顶点数
Array
path;
- path[i] 表示以 i 起始的最多顶点路径上经过的第一个顶点
Array
mark;
- 如果 i 起始的最多顶点路径已经找到,则: mark[i] 为 true
void init_array(Array &count, Array &path, Array &mark)
{
for (int i=0; i 寻找局部顶点数最多的路径
定义功能: search_max_path(v, count, path, mark)
- 以 v 作为起始顶点寻找最多顶点路径
- count 记录经过的最多定点数
- path 记录最多顶点路径上经过的第一个顶点
- mark 记录最多顶点路径是否已经找到
编程实验:局部最多顶点路径
// 求解局部最短路径
int search_max_path(Graph &g, int v, Array &count, Array &path, Array &mark)
{
int ret = 0;
int k = -1;
SharedPointer> aj = g.getAdjacent(v);
for (int i=0; ilength(); ++i)
{
int num = 0;
if (!mark[(*aj)[i]])
{
num = search_max_path(g, (*aj)[i], count, path, mark);
}
else
{
num = count[(*aj)[i]];
}
if (ret < num)
{
ret = num;
k = (*aj)[i];
}
}
++ret;
mark[v] = true;
count[v] = ret;
path[v] = k;
return ret;
}
// 求解全局最短路径
void search_max_path(Graph &g, Array &count, Array &path, Array &mark)
{
for (int i=0; i 最长不下降序列求解流程
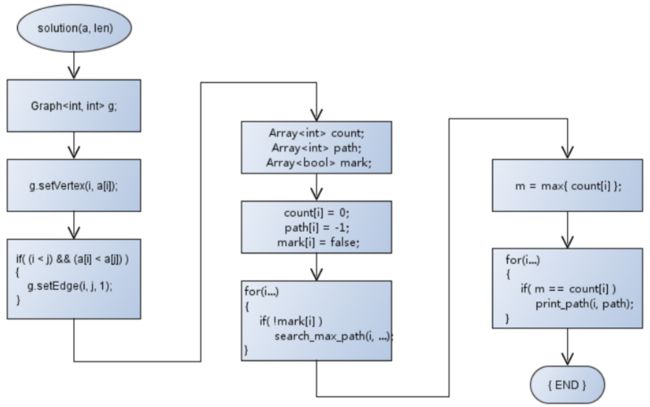
void solution(int *a, int len)
{
DynamicArray count(len);
DynamicArray path(len);
DynamicArray mark(len);
SharedPointer> g;
g = create_graph(a, len);
init_array(count, path, mark);
search_max_path(*g, count, path, mark);
print_max_path(*g, count, path);
} 编程实验:最长不下降序列
文件:main.cpp
#include
#include "ListGraph.h"
using namespace std;
using namespace DTLib;
SharedPointer> create_graph(int *a, int len)
{
ListGraph *ret = new ListGraph(len);
if (ret != nullptr)
{
for (int i=0; isetVertex(i, a[i]);
}
for (int i=0; i 保证相对位置不变 !!
{
if (a[i] <= a[j]) // 保证有序不下降
{
ret->setEdge(i, j, 1);
}
}
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create graph ...");
}
return ret;
}
void init_array(Array &count, Array &path, Array &mark)
{
for (int i=0; i &g, int v, Array &count, Array &path, Array &mark)
{
int ret = 0;
int k = -1;
SharedPointer> aj = g.getAdjacent(v);
for (int i=0; ilength(); ++i)
{
int num = 0;
if (!mark[(*aj)[i]])
{
num = search_max_path(g, (*aj)[i], count, path, mark);
}
else
{
num = count[(*aj)[i]];
}
if (ret < num)
{
ret = num;
k = (*aj)[i];
}
}
++ret;
mark[v] = true;
count[v] = ret;
path[v] = k;
return ret;
}
// 求解全局最短路径
void search_max_path(Graph &g, Array &count, Array &path, Array &mark)
{
for (int i=0; i &g, Array &count, Array &path)
{
int max = 0;
for (int i=0; i 求最长路径,总会存在最后一个顶点无后邻接顶点以成为结束条件
{
cout << g.getVertex(j) << " ";
}
cout << endl;
}
}
}
void solution(int *a, int len)
{
DynamicArray count(len);
DynamicArray path(len);
DynamicArray mark(len);
SharedPointer> g;
g = create_graph(a, len);
init_array(count, path, mark);
search_max_path(*g, count, path, mark);
print_max_path(*g, count, path);
}
int main()
{
int a[] = {3,18,7,14,10,12,23,41,16,24};
solution(a, sizeof (a)/sizeof(*a));
return 0;
} 输出:
Len :6
Element : 3 7 10 12 16 24最长不下降序列优化
描述
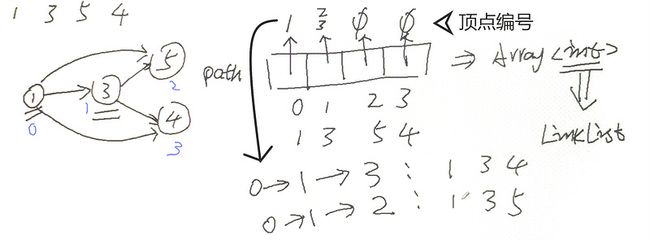
原数列:[1,3,5,4]
最长不下降序列:[1,3,5] [1,3,4]
int main()
{
int a[] = {1, 3, 5, 4};
solution(a, sizeof (a)/sizeof(*a));
return 0;
}输出:
Len :3
Element : 1 3 4问题: [1,3,5] 未输出
问题分析
path 为单维数组,无法保存更多路径顶点信息
解决方案
path 数组元素类型修改为: 顶点编号链表
编程实验:最长不下降序列优化
文件:main.cpp
#include
#include "ListGraph.h"
#include "LinkList.h"
using namespace std;
using namespace DTLib;
SharedPointer> create_graph(int *a, int len)
{
ListGraph *ret = new ListGraph(len);
if (ret != nullptr)
{
for (int i=0; isetVertex(i, a[i]);
}
for (int i=0; i 保证相对位置不变 !!
{
if (a[i] <= a[j]) // 保证有序不下降
{
ret->setEdge(i, j, 1);
}
}
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create graph ...");
}
return ret;
}
void init_array(Array &count, Array*> &path, Array &mark)
{
for (int i=0; i();
if (path[i] == nullptr)
{
THROW_EXCEPTION(InvalidOpertionExcetion, "No memory to create LinkList obj ...");
}
}
for (int i=0; i &g, int v, Array &count, Array*> &path, Array &mark)
{
int ret = 0;
SharedPointer> aj = g.getAdjacent(v);
for (int i=0; ilength(); ++i)
{
int num = 0;
if (!mark[(*aj)[i]])
{
num = search_max_path(g, (*aj)[i], count, path, mark);
}
else
{
num = count[(*aj)[i]];
}
if (ret < num)
{
ret = num;
}
}
for (int i=0; ilength(); ++i)
{
if (ret == count[(*aj)[i]])
{
path[v]->insert((*aj)[i]);
}
}
++ret;
mark[v] = true;
count[v] = ret;
return ret;
}
// 求解全局最短路径
void search_max_path(Graph &g, Array &count, Array*> &path, Array &mark)
{
for (int i=0; i &g, int v, Array &count, Array*> &path, LinkList &cp)
{
cp.insert(v);
if (path[v]->length() > 0)
{
for (path[v]->move(0); !path[v]->end(); path[v]->next())
{
print_path(g, path[v]->current(), count, path, cp);
}
}
else
{
cout << "Element : ";
for (cp.move(0); !cp.end(); cp.next())
{
cout << g.getVertex(cp.current()) << " ";
}
cout << endl;
}
cp.remove(cp.length()-1);
}
void print_max_path(Graph &g, Array &count, Array*> &path)
{
int max = 0;
LinkList cp;
for (int i=0; i count(len);
DynamicArray*> path(len);
DynamicArray mark(len);
SharedPointer> g;
g = create_graph(a, len);
init_array(count, path, mark);
search_max_path(*g, count, path, mark);
print_max_path(*g, count, path);
}
int main()
{
int a[] = {1, 3, 5, 4};
solution(a, sizeof (a)/sizeof(*a));
return 0;
} 输出:
Len :3
Element : 1 3 4
Element : 1 3 5以上内容整理于狄泰软件学院系列课程,请大家保护原创!