什么是“Trie树”?
Trie树,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
核心思想
空间换时间,利用字符串的公共前缀来减少无谓的字符串比较以达到提高查询效率的目的。
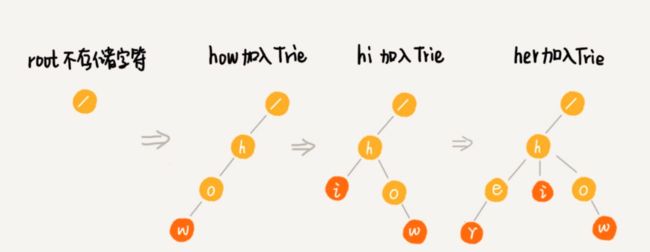
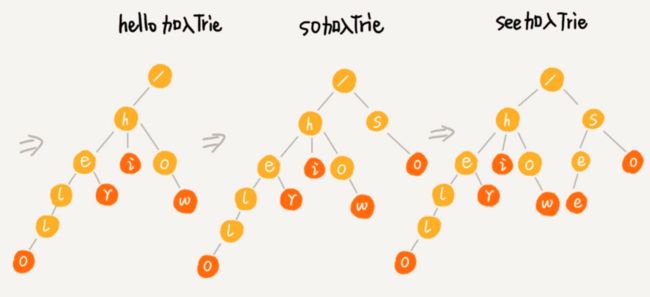
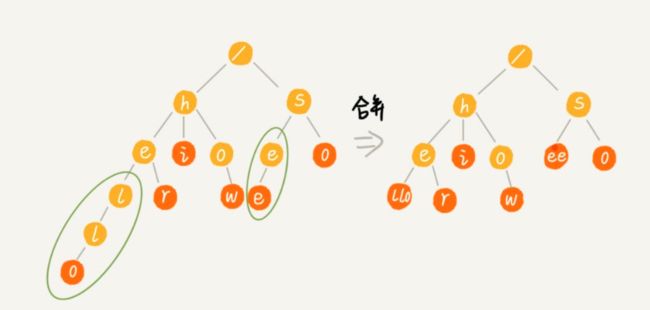
构建流程图解
其中,根节点不包含任何信息。每个节点表示一个字符串中的字符,从根节点到红色节点的一条路径表示一个字符串(注意:红色节点并不都是叶子节点)。
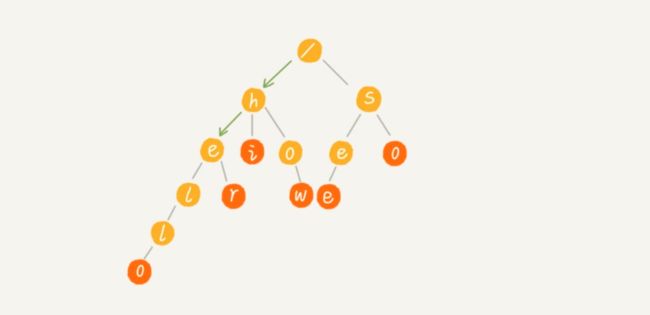
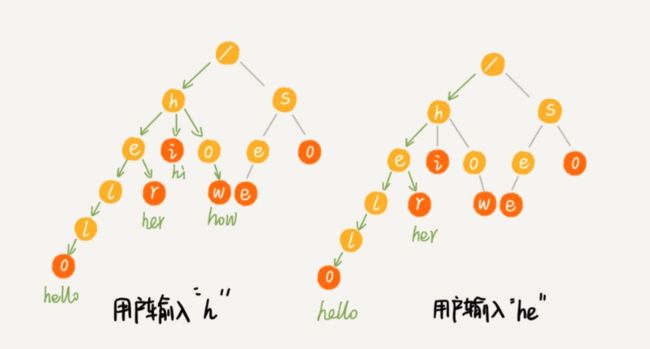
当我们在Trie树中查找一个字符串的时候,比如查找字符串“her”,那我们将要查找的字符串分割成单个的字符h,e,r,然后从Trie树的根节点开始匹配。如图所示,绿色的路 径就是在Trie树中匹配的路径。
如何实现一棵Trie树?
从刚刚Trie树的介绍来看,Trie树主要有两个操作,一个是将字符串集合构造成Trie树。这个过程分解开来的话,就是一个将字符串插入到Trie树的过程。另一个是在Trie树中 查询一个字符串。
了解了Trie树的两个主要操作之后,那么如何存储一个多叉树,Trie树呢?
经典的存储方式
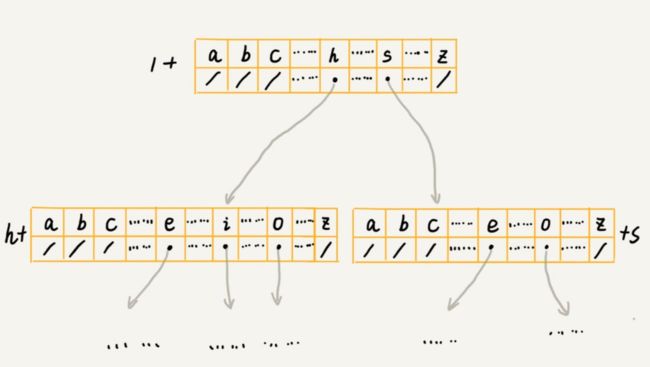
一种比较经典的存储方式,借助散列表的思想,我们通过一个下标与 字符一一映射的数组,来存储子节点的指针。如下图所示:
假设我们的字符串中只有从a到z这26个小写字母,我们在数组中下标为0的位置,存储指向子节点a的指针,下标为1的位置存储指向子节点b的指针,以此类推,下标为25的位 置,存储的是指向的子节点z的指针。如果某个字符的子节点不存在,我们就在对应的下标的位置存储null。
当我们在 trie树中查找字符串的时候,我们就可以通过字符的 ASCII 码减去 'a' 的 ASCII码,迅速找到匹配的子节点的指针。比如,'d' 的 ASCII码减去'a' 的 ASCII码就是 3,那子节 点d的指针就存储在数组中下标为3的位置中。
package main
import (
"fmt"
)
type TrieNode struct {
Value string
Children []*TrieNode
IsEndingChar bool //结束节点字符标识
}
func NewTrieNode(val string) *TrieNode {
return &TrieNode{Value: val, Children: make([]*TrieNode, 26, 26)}
}
type Trie struct {
Root *TrieNode
}
func NewTrie() *Trie {
return &Trie{Root: NewTrieNode("/")}
}
func (trie *Trie) insert(text string) {
p := trie.Root
for _, v := range text {
index := v - 'a' // 'a' 等于 95 ,'b'-'a' = 1 这里计算出 v 应该存储的索引
if p.Children[index] == nil { // 不存在该点
node := NewTrieNode(string(v))
p.Children[index] = node
}
p = p.Children[index] // 走向下一个节点
}
p.IsEndingChar = true // 标识该节点结束节点
}
func (trie *Trie) find(text string) bool {
p := trie.Root
for _, v := range text {
index := v - 'a' // 'a' 等于 95 ,'b'-'a' = 1 这里计算出 v 应该存储的索引
if p.Children[index] == nil {
return false
}
p = p.Children[index] // 走向下一个节点
}
return p.IsEndingChar
}
func (trie *Trie) likeFind(text string) [] string {
res := make([]string, 0, 0)
p := trie.Root
for _, v := range text {
index := v - 'a' // 'a' 等于 95 ,'b'-'a' = 1 这里计算出 v 应该存储的索引
if p.Children[index] == nil {
return res
}
p = p.Children[index] // 走向下一个节点
}
if p.IsEndingChar {
res = append(res, text)
}
strings, _ := like(p, res, text)
return strings
}
func like(p *TrieNode, res []string, path string) ([]string, string) {
//fmt.Println("root is ", p.Value, res, path)
for _, v := range p.Children {
if v != nil {
path += v.Value
//fmt.Printf("path is %s %s\n", p.Value, path)
res, path = like(v, res, path)
}
}
if p.IsEndingChar {
res = append(res, path)
}
path = path[:len(path)-1]
return res, path
}
func main() {
trie := NewTrie()
trie.insert("how")
trie.insert("hi")
trie.insert("her")
trie.insert("hello")
trie.insert("so")
trie.insert("see")
trie.insert("word")
for _, v := range []string{"hello", "baozi", "see", "li", "hai", "le", "word", "ge"} {
fmt.Printf("find %v ,%v \n", v, trie.find(v))
}
for _, v := range []string{"h", "he", "hi", "s"} {
strings := trie.likeFind(v)
fmt.Printf("输入:%s , 提示:%v\n", v, strings)
}
}
时间复杂度
如果要在一组字符串中,频繁地查询某些字符串,用Trie树会非常高效。构建Trie树的过程,需要扫描所有的字符串,时间复杂度是O(n)(n表示所有字符串的长度和)。但是 一旦构建成功之后,后续的查询操作会非常高效。
每次查询时,如果要查询的字符串长度是k,那我们只需要比对大约k个节点,就能完成查询操作。跟原本那组字符串的长度和个数没有任何关系。所以说,构建好Trie树后, 在其中查找字符串的时间复杂度是O(k),k表示要查找的字符串的长度。
空间复杂度
按上面的示例,是有点恐怖的。
Trie树真的很耗内存吗?
是的,它这很耗内存。核心思想就是空间换时间。
前面我们讲了Trie树的实现,也分析了时间复杂度。现在你应该知道,Trie树是一种非常独特的、高效的字符串匹配方法。但是,关于Trie树,你有没有听过这样一种说
刚刚我们在讲Trie树的实现的时候,讲到用数组来存储一个节点的子节点的指针。如果字符串中包含从a到z这26个字符,那每个节点都要存储一个长度为26的数组,并且每个 数组存储一个8字节指针(或者是4字节,这个大小跟CPU、操作系统、编译器等有关)。而且,即便一个节点只有很少的子节点,远小于26个,比如3、4个,我们也要维护一个长度为26的数组。 我们前面讲过,Trie树的本质是避免重复存储一组字符串的相同前缀子串,但是现在每个字符(对应一个节点)的存储远远大于1个字节。按照我们上面举的例子,数组长度
为26,每个元素是8字节,那每个节点就会额外需要26*8=208个字节。而且这还是只包含26个字符的情况。 如果字符串中不仅包含小写字母,还包含大写字母、数字、甚至是中文,那需要的存储空间就更多了。所以,也就是说,在某些情况下,Trie树不一定会节省存储空间。在重复的前缀并不多的情况下,Trie树不但不能节省内存,还有可能会浪费更多的内存。 当然,我们不可否认,Trie树尽管有可能很浪费内存,但是确实非常高效。
解决办法
我们可以稍微牺牲一点查询的效率,将每个节点中的数组换成其他数据结构,来存储一个节点的子节点指针。用哪种数据结构呢?我们的选择其实有很多,比如有序数组、跳
表、散列表、红黑树等。
假设我们用有序数组,数组中的指针按照所指向的子节点中的字符的大小顺序排列。查询的时候,我们可以通过二分查找的方法,快速查找到某个字符应该匹配的子节点的指 针。但是,在往Trie树中插入一个字符串的时候,我们为了维护数组中数据的有序性,就会稍微慢了点。
替换成其他数据结构的思路是类似的。
实际上,Trie树的变体有很多,都可以在一定程度上解决内存消耗的问题。比如,缩点优化,就是对只有一个子节点的节点,而且此节点不是一个串的结束节点,可以将此节 点与子节点合并。这样可以节省空间,但却增加了编码难度。(还没来得及研究)
Trie树与散列表、红黑树的比较
实际上,字符串的匹配问题,笼统上讲,其实就是数据的查找问题。对于支持动态数据高效操作的数据结构,我们前面已经讲过好多了,比如散列表、红黑树、跳表等等。实际上,这些数据结构也可以实现在一组字符串中查找字符串的功能。我们选了两种数据结构,散列表和红黑树,跟Trie树比较一下,看看它们各自的优缺点和应用场景。 示例代码中,在一组字符串中查找字符串,Trie树实际上表现得并不好。它对要处理的字符串有及其严苛的要求。
第一,字符串中包含的字符集不能太大。如果字符集太大,那存储空间可能就会浪费很多。即便可以优化,但也要付出牺牲查询、插入效率的代价。
第二,要求字符串的前缀重合比较多,不然空间消耗会变大很多。
第三,如果要用Trie树解决问题,那我们就要自己从零开始实现一个Trie树,还要保证没有bug,这个在工程上是将简单问题复杂化,除非必须,一般不建议这样做。
第四,通过指针串起来的数据块是不连续的,而Trie树中用到了指针,所以,对缓存并不友好,性能上会打个折扣。综合这几点,针对在一组字符串中查找字符串的问题,我们在工程中,更倾向于用散列表或者红黑树。因为这两种数据结构,我们都不需要自己去实现,直接利用编程语言中提供的现成类库就行了。
结论
Trie树是一种解决字符串快速匹配问题的数据结构。如果用来构建Trie树的这一组字符串中,前缀重复的情况不是很多,那Trie树这种数 据结构总体上来讲是比较费内存的,是一种空间换时间的解决问题思路。
尽管比较耗费内存,但是对内存不敏感或者内存消耗在接受范围内的情况下,在Trie树中做字符串匹配还是非常高效的,时间复杂度是O(k),k表示要匹配的字符串的长度。 但是,Trie树的优势并不在于,用它来做动态集合数据的查找,因为,这个工作完全可以用更加合适的散列表或者红黑树来替代。Trie树最有优势的是查找前缀匹配的字符
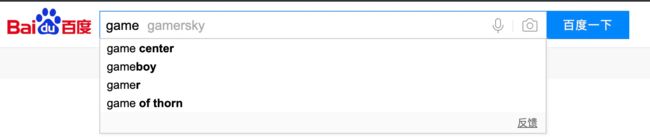
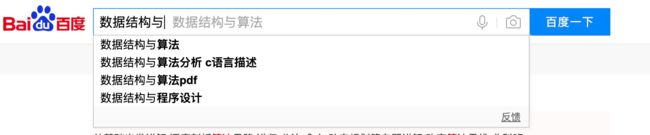
串,比如搜索引擎中的关键词提示功能这个场景,就比较适合用它来解决,也是Trie树比较经典的应用场景。
假设关键词库由用户的热门搜索关键词组成。我们将这个词库构建成一个Trie树。当用户输入其中某个单词的时候,把这个词作为一个前缀子串在Trie树中匹配。为了讲 解方便,我们假设词库里只有hello、her、hi、how、so、see这6个关键词。当用户输入了字母h的时候,我们就把以h为前缀的hello、her、hi、how展示在搜索提示框内。当用户 继续键入字母e的时候,我们就把以he为前缀的hello、her展示在搜索提示框内。这就是搜索关键词提示的最基本的算法原理。
实际应用场景
中文trie用示例中的方式实现你会奔溃的。需要另想它法。ÅåΩå