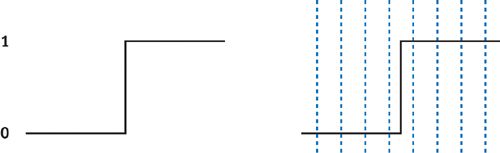令人讨厌的“走样”
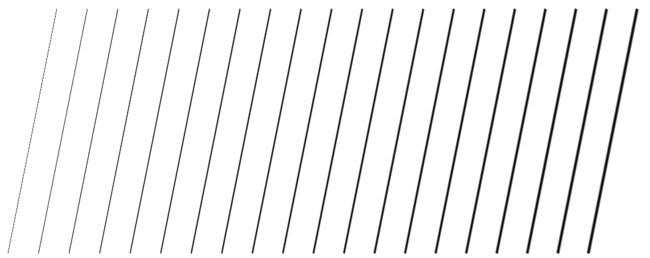
我在日常工作中通过传统的OpenGL绘制函数绘制线段时,发现绘制出的线段边缘充满了“锯齿”,而这种“锯齿”在线段运动和旋转时往往会更加明显(图 1)。这种我们不希望看到的“锯齿”被成为“走样”,而消除这种“锯齿”的过程就是我们所说的“反走样”。虽然OpenGL提供了诸如设置 GL_LINE_SMOOTH 属性、多重采样等线段反走样的方法,但效果和质量受到很多方面的限制,而且不同的硬件厂商使用不同的反走样算法,所以使得反走样的结果在不同的GPU上有 着不同的效果。因此我们需要一种更为高效和通用的线段反走样技术。
为什么会“走样”?
在介绍如何对线段反走样之前,我们必须了解为什么我们绘制的线段会产生“走样”。
我们都知道,在数学的定义中一条线段是由两个端点确定的,而线段是没有宽度和面积的。但在计算机图形领域中,为了让人的肉眼能够看到,必须给线段一定的宽 度,所以我们的线段通常是由两个端点和一个宽度参数确定的,而我们计算机中图形的宽度通常都是以像素为单位的,因此我们的线段宽度有可能是1像素也有可能 是n像素。
如果需要在白色的背景下绘制一条宽度为1像素的黑色线段,从信号处理的观点上来看,我们可以把这条线段看做一个值为1的信号,而线段外部的区域信号值为0,如果不加任何处理,线段的边界就是这样一个不连续的阶梯函数(图2)。 因为帧缓存和显示器所能容纳的像素点是有限的,所以我们需要对这个信号进行采样。
我们可以看到:离散采样(图2 中用蓝色虚线表示)的间隔无论多么的小都无法精确的表达它的不连续性,因此我们无论怎么提高分辨率,都无法彻底消除走样。而根据耐奎斯特的信号采样定理:要重构一个不走样的信号,采样率至少是信号最高频率的两倍。
即:C = B * log2 N ( bps )
因此,从理论上来说要绘制一条没有走样的线段,我们必须拥有足够大的信号频率,也就是我们需要无限放大我们的屏幕分辨率才能彻底消除走样。
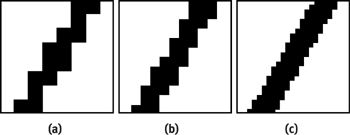
从图3我们可以看出,虽然我们提高了分辨率,但是走样依然存在。因此,一味地提高分辨率是无法彻底解决掉线段走样问题的,而且在时间、空间以及金钱有限的情况下是不允许我们这么做的。
解决之道
计算机图形学领域中广泛采用的一种方法是:限制信号的带宽。也就是说既然无法提高分辨率,我们可以将信号中无法还原的高频部分去掉以达到“反走样”的目的。这样线段就不再有明显尖锐的边界了,相反,线段的边界处将变得模糊,这种将边界模糊的过程我们称之为“过滤”。我们可以让信号通过一个低通过滤器,来过滤掉信号中的高频部分,以达到过滤的效果,这样的过滤器有很多,可以是简单的线性过滤器也可以是稍微复杂一点的盒状过滤器或高斯过滤器。本文将以高斯过滤器为例,为大家介绍整个过滤的过程。
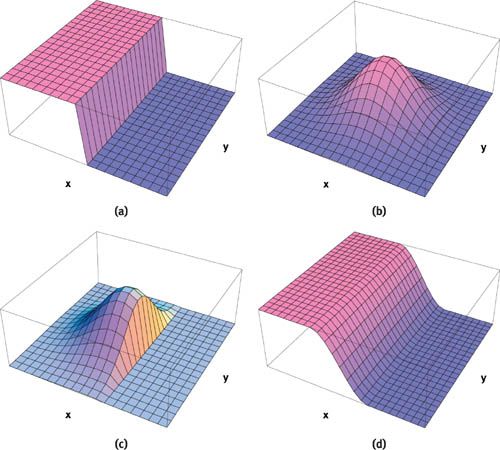
图4演示了高斯过滤器对一个2D信号进行过滤操作的整个过程,首先图4(a)表示未处理的线段信号,其中x和y轴表示线段所处平面坐标系,z轴表示图像信号的强度,可以认为是RGBA颜色中的alpha值。其中左半部分z=1表示位于线段内部,右半部份z=0表示位于线段外部,这里z=0和z=1边界处是不连续的。图4(b)所表示的是一个高斯地同过滤器,将它与图4(a)中的某一段信号做卷积后就得到了图4(c)中的效果。卷积在这里等效于求出过滤器与信号相交部分的体积,图4(d)就是将所有信号与过滤器卷积后得到的最终过滤效果。
从图5可以看到:经过过滤后的线段边界将不再是一段不连续的阶梯函数,而是一段连续的平滑曲线。
预处理
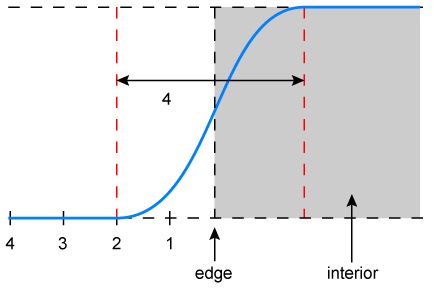
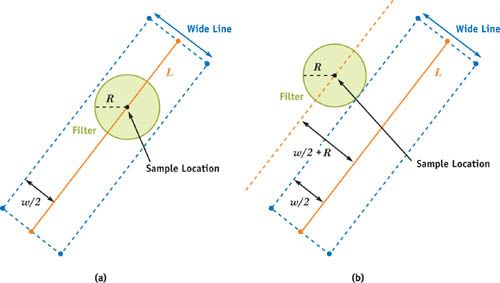
如图6所示,在预处理过程中,我们将半径为R的过滤器和宽度为W的线段进行卷积,所得到的强度值根据过滤器的位置变化而变化。当过滤器刚好位于直线上(图6a)时,我们得到的强度值最大,因为此时过滤器与直线重叠部分最多,(在图4所示坐标系中)重叠部分的体积也就越大。相反的,当过滤器位于距离直线w/2+R的位置(图6b)时,卷积所得强度值最小,因为此时过滤器与直线没有重叠。而在过滤器从距离为0移动到w/2+R处的过程中,强度值在慢慢变小。
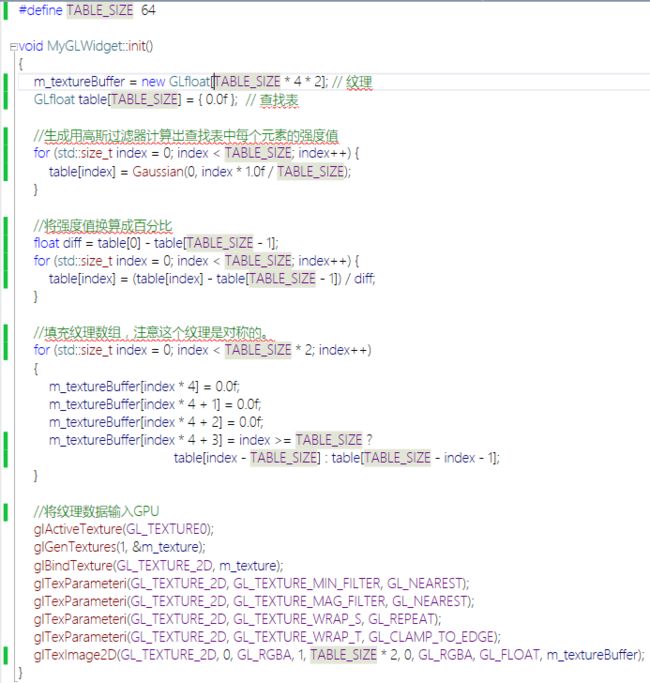
然而,我们并不希望计算量会随线段宽度变化,我们希望我们的渲染过程的效率是稳定的,因此,我们需要一张固定宽度的查找表。通过实践发现,一张32个强度值的查找表已经足够应付任意宽度的直线了(图7),如果觉得这样不够精细,你还可以使用64个强度值的查找表,因为对于GPU来说,处理一个32或64元素的1D纹理实在是小菜一碟。
如图8中的代码片段所示,生成这样一个纹理只需按照设定的强度值数量利用过滤器计算出相应数量的强度值就可以了。唯一需要注意的是这个纹理是关于直线中心对称的,以及纹理参数中缩放过滤参数要设置为GL_NEAREST。
运行时
预处理只需要在CPU中运行一次,而当我们将过滤后的纹理完成后,我们的预处理工作就算告一段落,接下来就可以进行渲染了。渲染时,我们需要进行两种计算,一种是在CPU中的线段相关参数的计算,另一种计算GPU的着色器中进行的,主要是利用CPU提供的参数在顶点着色器和片段着色器中计算出真正的位置和颜色。
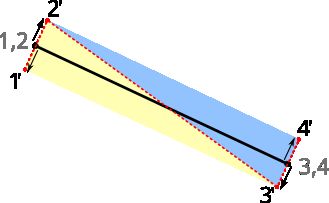
计算矩形顶点的坐标看起来也不是一件很困难的事情,只需要将线段的两个顶点向两侧分别平移w/2距离就可以得到(图9),而线段的平移方向正好是xy平面上垂直于该线段的法向量方向,因此我们只需要计算这个法向量即可。
有了法向量后,顶点着色器中只需将顶点和法向量相乘,再乘上w/2就可以得到平移后的顶点位置,最后再与线段的模型视图投影矩阵相乘,计算出最终的顶点位置(图10)。
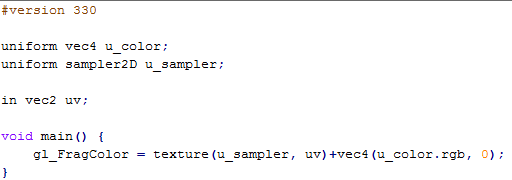
片段着色器只需对纹理进行一次采样得到强度值再与线段颜色进行一次叠加就行了,这样就能得到一条任意颜色的线段。
最终效果
并且对它进行拉伸或者旋转都不会产生新的走样(图13)。
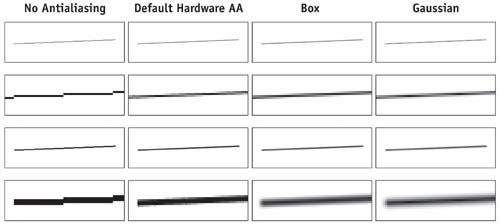
通过图13的对比我们可以清楚地看出,经过预过滤反走样处理的线段相比普通线段和硬件反走样处理的线段锯齿感明显要弱了许多。这种处理方式所需的存储空间代价仅仅是额外的两个顶点和一个宽度64的一维纹理,而运行时处理上也只是增加了一次法向量的计算,可以称得上是简单高效。
最后,希望这个方法能够对大家处理2D线段抗锯齿问题能够有所帮助,如果对有对这方面研究感兴趣的朋友,欢迎加入我们进行讨论(QQ群:280689979)。