基本思路
首先,用户输入的待求表达式,也就是中缀表达式,对于人来说,这个很好理解,但是对于计算机,后缀表达式求值更加容易。如果看成一棵二叉树,其实中缀表达式就是对一个二叉树的中序遍历,后缀表达式(也叫逆波兰表达式)就是后序遍历的结果。那么主要思路就来了:先把中缀表达式转换成后缀表达式,再对后缀表达式进行求值。
步骤一,中缀表达式转后缀表达式
两个数据结构:
1,后缀表达式队列
用于存放最后的后缀表达式
2,操作符栈
对用户输入的操作符进行处理
算法伪代码:
/*
依次读入用户输入的中缀表达式
如果是数字,直接入队
如果是操作符,如果栈为空,直接入栈
如果操作符为 ( 直接入栈
如果操作符为 ) ,依次出栈,直到遇到第一个(,(和)都不入栈
如果是其他操作符(+ - * /),则和栈顶元素进行比较优先级
如果栈顶元素优先级大于等于(*和/ > +和-)操作符 ,则出栈,直到栈顶元素优先级小于操作符或栈为空
*/
//伪代码
//后缀表达式队列
queue num;
//操作符栈
stack option;
while(scanf("%c",&x)){
if(x 是数){
num.addBack(x); //入队
}else if(option.empty() || x == '('){
//如果栈为空,直接入栈,如果操作符为 ( 直接入栈
option.push(x)
}else if(x == ')'){
//如果操作符为 ) ,依次出栈,直到遇到第一个(,(和)都不入栈
while((tmp = option.pop()) != '('){
num.addBack(tmp);
}
}else{
//只是获取栈首元素,没有出栈
while(1){
tmp = option.head();
if(tmp 优先级大于等于x){
tmp1 = option.pop();
num.addBack(tmp1);
}else{
break;
}
}
option.push(x);
}
}
//最后把所有操作符入队
while(!option.empty()){
tmp = option.pop();
num.addBack(tmp);
}
步骤二,后缀表达式计算值
数据结构:
结果栈
用于存放计算的中间过程的值和最终结果
算法伪代码:
/*
依次从后缀表达式队列中取值
如果是值,直接入栈
如果是操作符,从队列中取出两个数,进行运算(后取出来的数作为第一个运算符),计算结果再次压栈
*/
//用于存放结果的栈
stack res;
//后缀表达式队列,上一步求出来的
queue num;
while(!num.empty()){
//取队首
tmp = num.getFront();
if(tmp 是数){
res.push(tmp);
}else{
num1 = num.pop();
num2 = num.pop();
num3 = num2 tmp num1;
res.push(num3);
}
}
步骤三,转二叉树
算法伪代码:
/*
主要是在计算逆波兰表达式的时候,构造出一棵二叉树,
构造思路和计算时差不多,如果是数,就直接构造节点,如果是操作符,就把前面两个节点提出来作为左右节点
*/
//用于存放所有临时节点和最后根节点的数组
treeNode all[MAX];
int n=0;
//后缀表达式队列,上一步求出来的
queue num;
while(!num.empty()){
//取队首
tmp = num.getFront();
if(tmp 是数){
res[n++] = tmp;
}else{
num1 = all[--n];
num2 = all[--n];
tmp.left = num1;
tmp.right = num2;
all[n++] = tmp;
}
}
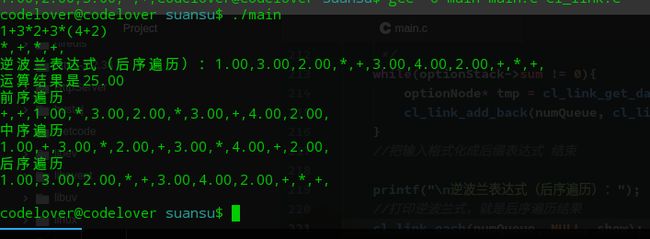
运行情况
完整代码
/**
* 计算算术表达式的值,支持 加减乘除括号 运算
* 思路是,先把用户输入的表达式(中缀表达式,中序遍历),格式化成逆波兰表达式(后缀表达式,后序遍历序列)
* 再对后缀表达式进行求值
*/
#include
#include
//通用链表
#include "cl_link.h"
#define MAX 1024
#define IS_OPTION '0'
#define IS_NUM '1'
char* optionAll = "+-*/()";
typedef struct bTree{
char type;
double num;
char option;
struct bTree* left;
struct bTree* right;
}bTree;
//运算符节点
typedef struct optionNode{
//用于标志运算符
char type;
cl_link_node node;
char option;
}optionNode;
//操作数节点
typedef struct numNode{
// 用于标志操作数
char type;
cl_link_node node;
double num;
}numNode;
//运算符栈
cl_link* optionStack = NULL;
//数字队列
cl_link* numQueue = NULL;
/**
* 比较是否是运算符
* @param optionAll 运算符表
* @param aim 比较对象
* @return 1 是 0 不是
*/
int isOption(const char* optionAll,const char aim)
{
for (size_t i = 0; i < strlen(optionAll); i++) {
if(aim == *(optionAll+i)){
return 1;
}
}
return 0;
}
/**
* 比较优先级
* @return 1 src >= des
* 0 src < des
*/
int isMaxLevel(const char src, const char des)
{
if(src == '*' || src == '/')
return 1;
if((src == '+' || src == '-') && (des == '+' || des == '-'))
return 1;
return 0;
}
void* show(void* arg)
{
numNode* node = cl_link_get_data(arg, numNode, node);
if(node->type == IS_NUM){
printf("%0.2f,", node->num);
}else{
optionNode* node1 = cl_link_get_data(arg, optionNode, node);
printf("%c,", node1->option);
}
return NULL;
}
//计算
double cal(double num1, double num2, char option)
{
switch (option) {
case '+':
return num1+num2;
case '-':
return num1-num2;
case '*':
return num1*num2;
case '/':
return num1/num2;
}
return 0;
}
void pre(bTree* root){
if(root != NULL)
{
if(root->type == IS_NUM){
printf("%0.2f,", root->num);
}else{
printf("%c,", root->option);
}
pre(root->left);
pre(root->right);
}
}
void mid(bTree* root){
if(root != NULL)
{
mid(root->left);
if(root->type == IS_NUM){
printf("%0.2f,", root->num);
}else{
printf("%c,", root->option);
}
mid(root->right);
}
}
void back(bTree* root){
if(root != NULL)
{
back(root->left);
back(root->right);
if(root->type == IS_NUM){
printf("%0.2f,", root->num);
}else{
printf("%c,", root->option);
}
}
}
int main()
{
//初始化运算符栈
optionStack = cl_link_create();
//初始化逆波兰空队列,即后序遍历结果
numQueue = cl_link_create();
//把输入格式化成后缀表达式 开始
char expr[MAX];
scanf("%s", expr);
for (size_t i = 0; i < strlen(expr); i++) {
//假设输入完全合法,不是运算符就是运算数
if(!isOption(optionAll, *(expr+i))){
//运算数,直接入队,numQueue
numNode* node = malloc(sizeof(numNode));
node->num = atoi(expr+i);
node->type = IS_NUM;
int tmp = node->num;
while(tmp/10 > 0){
i++;
tmp /= 10;
}
//入队
cl_link_add_back(numQueue, cl_link_get_node(node, numNode, node));
}else{
/**
* 如果栈为空,直接入栈
* 如果是( 直接入栈
* 如果是) 则依次出栈到队列中,直到遇到第一个(
* 如果X是其他运算符,则依次与栈顶元素比较优先级,
* 如果栈顶元素的优先级大于等于X,
* 则出栈,直到栈顶元素的优先级小于X或者栈为空。
* 否则 入栈
*/
optionNode* node = malloc(sizeof(optionNode));
node->type = IS_OPTION;
node->option = *(expr+i);
if(optionStack->sum == 0 || *(expr+i) == '('){
//如果栈为空,或者是(,直接入栈
cl_link_push(optionStack, cl_link_get_node(node, optionNode, node));
}else if(*(expr+i) == ')'){
//如果是) 则依次出栈到队列中,直到遇到第一个(
while(1){
optionNode* tmp = cl_link_get_data(cl_link_pop(optionStack), optionNode, node);
if(tmp->option == '('){
break;
}else{
cl_link_add_back(numQueue, cl_link_get_node(tmp, optionNode, node));
}
}
}else{
printf("%C,", *(expr+i));
//如果X是其他运算符,则依次与栈顶元素比较优先级,如果栈顶元素的优先级大于等于X,则出栈,直到栈顶元素的优先级小于X或者栈为空。
while(1){
//得到栈顶元素
optionNode* tmp = cl_link_get_data(cl_link_get_head(optionStack), optionNode, node);
if(isMaxLevel(tmp->option, *(expr+i))){
//如果优先级大于运算符,就出栈到逆波兰队列
optionNode* tmp = cl_link_get_data(cl_link_pop(optionStack), optionNode, node);
cl_link_add_back(numQueue, cl_link_get_node(tmp, optionNode, node));
}else{
break;
}
}
optionNode* node = malloc(sizeof(optionNode));
node->type = IS_OPTION;
node->option = *(expr+i);
cl_link_push(optionStack, cl_link_get_node(node, optionNode, node));
}
}
}
/**
* 若运算符还有,则直接出栈
*/
while(optionStack->sum != 0){
optionNode* tmp = cl_link_get_data(cl_link_pop(optionStack), optionNode, node);
cl_link_add_back(numQueue, cl_link_get_node(tmp, optionNode, node));
}
//把输入格式化成后缀表达式 结束
printf("\n逆波兰表达式(后序遍历):");
//打印逆波兰式,就是后序遍历结果
cl_link_each(numQueue, NULL, show);
bTree* allTreeNode[MAX];
int n = 0;
//计算逆波兰表达式结果,用于存放临时结果和最终结果
cl_link* res = cl_link_create();
while(numQueue->sum != 0){
numNode* tmp = cl_link_get_data(cl_link_pop(numQueue), numNode, node);
if(tmp->type == IS_NUM){
//如果是数,直接入栈
cl_link_push(res, cl_link_get_node(tmp, numNode, node));
bTree* newNode = malloc(sizeof(bTree));
newNode->left = NULL;
newNode->right = NULL;
newNode->type = IS_NUM;
newNode->num = tmp->num;
allTreeNode[n++] = newNode;
}else{
//如果是操作符,则pop出栈顶两个元素,进行运算,再入栈
optionNode* tmpOption = (optionNode*)tmp;
numNode* num1 = cl_link_get_data(cl_link_pop(res), numNode, node);
numNode* num2 = cl_link_get_data(cl_link_pop(res), numNode, node);
numNode* node = malloc(sizeof(numNode));
node->num = cal(num2->num, num1->num, tmpOption->option);
node->type = IS_NUM;
cl_link_push(res, cl_link_get_node(node, numNode, node));
bTree* newNode = malloc(sizeof(bTree));
newNode->left = NULL;
newNode->right = NULL;
newNode->type = IS_OPTION;
newNode->option = tmpOption->option;
newNode->right = allTreeNode[--n];
newNode->left = allTreeNode[--n];
allTreeNode[n++] = newNode;
}
}
numNode* resData = cl_link_get_data(cl_link_get_head(res), numNode, node);
printf("\n运算结果是%0.2f\n", resData->num);
printf("前序遍历\n");
pre(allTreeNode[0]);
printf("\n中序遍历\n");
mid(allTreeNode[0]);
printf("\n后序遍历\n");
back(allTreeNode[0]);
printf("\n\n");
return 0;
}
涉及的队列和栈数据结构代码
cl_link.h
#ifndef _CL_LINK_H
#define _CL_LINK_H
#include
#include
#include
#include
#define ADD_SUCCESS (0)
#define ADD_FAIL (-1)
#define DELETE_SUCCESS (0)
#define SELETE_FAIL (-1)
#define CANFIND (1)
#define NOTFIND (0)
typedef struct cl_link_node cl_link_node;
typedef struct cl_link cl_link;
/**
* 链表节点,其他结构体需要使用链表数据结构,只需包含此节点
* @return
*/
typedef struct cl_link_node{
cl_link_node* next;
cl_link_node* prev;
}cl_link_node;
/**
* 通用链表对象
* @return
*/
typedef struct cl_link{
pthread_mutex_t cl_link_mutex; //链表锁
cl_link_node cl_link_head; //链表头
cl_link_node cl_link_tail; //链表尾
int sum; //节点数
}cl_link;
#define cl_link_get_node(aim, type, node) \
(cl_link_node *) ((u_char *) aim + offsetof(type, node))
#define cl_link_get_data(aim, type, node) \
(type *) ((u_char *) aim - offsetof(type, node))
/**
* 创建一个链表对象
* @return 链表对象地址
*/
cl_link* cl_link_create();
/**
* 链表的压栈操作
* @param link 链表对象
* @param node 新节点
* @return 压栈状态
*/
int cl_link_push(cl_link* link, void* node);
/**
* 链表的出栈操作
* @param link 链表对象
*/
void* cl_link_pop(cl_link* link);
//获取栈顶元素
void* cl_link_get_head(cl_link* link);
/**
* 对每个节点进行操作
* @param link 链表对象
* @param res 返回值
* @param handler 处理函数
*/
void cl_link_each(cl_link* link, void* res[], void* (*handler)(void* node));
/**
* 队尾添加元素
* @param link 队列对象
* @param node 新节点
* @return 添加状态
*/
int cl_link_add_back(cl_link* link, void* node);
/**
* 队头获取元素
* @param link 队列对象
* @return 取得的元素
*/
void* cl_link_get_front(cl_link* link);
/**
* 根据key查找节点
* @param link 链表对象
* @param key 关键字
* @param condition 条件
*/
void* cl_link_find(cl_link* link, void* key, int (*condition)(void* node, void* key));
#endif
cl_link.c
#include "cl_link.h"
/**
* 创建一个链表对象
* @return 链表对象地址
*/
cl_link* cl_link_create()
{
cl_link* link = malloc(sizeof(cl_link));
if(link == NULL){
write(STDERR_FILENO, "malloc error", sizeof("malloc error"));
return NULL;
}
pthread_mutex_init(&(link->cl_link_mutex), NULL);
pthread_mutex_lock(&(link->cl_link_mutex));
link->cl_link_head.next = &(link->cl_link_tail);
link->cl_link_head.prev = &(link->cl_link_tail);
link->cl_link_tail.next = &(link->cl_link_head);
link->cl_link_tail.prev = &(link->cl_link_head);
link->sum = 0;
pthread_mutex_unlock(&(link->cl_link_mutex));
return link;
}
/**
* 链表的压栈操作
* @param link 链表对象
* @param node 新节点
* @return 压栈状态
*/
int cl_link_push(cl_link* link, void* node)
{
cl_link_node* new_node = (cl_link_node*)node;
pthread_mutex_lock(&(link->cl_link_mutex));
if(link)
{
new_node->next = link->cl_link_head.next;
link->cl_link_head.next->prev = new_node;
link->cl_link_head.next = new_node;
new_node->prev = &(link->cl_link_head);
link->sum++;
pthread_mutex_unlock(&(link->cl_link_mutex));
return ADD_SUCCESS;
}else{
pthread_mutex_unlock(&(link->cl_link_mutex));
return ADD_FAIL;
}
}
/**
* 链表的出栈操作
* @param link 链表对象
*/
void* cl_link_pop(cl_link* link)
{
pthread_mutex_lock(&(link->cl_link_mutex));
if(link->sum){
cl_link_node* aim = link->cl_link_head.next;
link->cl_link_head.next = aim->next;
aim->next->prev = &(link->cl_link_head);
link->sum--;
pthread_mutex_unlock(&(link->cl_link_mutex));
return aim;
}else{
pthread_mutex_unlock(&(link->cl_link_mutex));
return NULL;
}
}
void* cl_link_get_head(cl_link* link)
{
return link->cl_link_head.next;
}
/**
* 对每个节点进行操作
* @param link 链表对象
* @param res 返回值
* @param handler 处理函数
*/
void cl_link_each(cl_link* link, void* res[], void* (*handler)(void* node))
{
pthread_mutex_lock(&(link->cl_link_mutex));
int n = link->sum;
void* r;
cl_link_node* p = link->cl_link_head.next;
cl_link_node* todo = p;
while(n)
{
todo = p;
p = p->next;
r = handler(todo);
if(res != NULL)
{
res[link->sum-n] = r;
}
n--;
}
pthread_mutex_unlock(&(link->cl_link_mutex));
}
/**
* 队尾添加元素
* @param link 队列对象
* @param node 新节点
* @return 添加状态
*/
int cl_link_add_back(cl_link* link, void* node)
{
cl_link_node* new_node = (cl_link_node*)node;
pthread_mutex_lock(&(link->cl_link_mutex));
if(link)
{
new_node->next = &(link->cl_link_tail);
new_node->prev = link->cl_link_tail.prev;
link->cl_link_tail.prev->next = new_node;
link->cl_link_tail.prev = new_node;
link->sum++;
pthread_mutex_unlock(&(link->cl_link_mutex));
return ADD_SUCCESS;
}else{
pthread_mutex_unlock(&(link->cl_link_mutex));
return ADD_FAIL;
}
}
/**
* 队头获取元素
* @param link 队列对象
* @return 取得的元素
*/
void* cl_link_get_front(cl_link* link)
{
return cl_link_pop(link);
}
/**
* 根据key查找节点
* @param link 链表对象
* @param key 关键字
* @param condition 条件
*/
void* cl_link_find(cl_link* link, void* key, int (*condition)(void* node, void* key))
{
pthread_mutex_lock(&(link->cl_link_mutex));
int n = link->sum;
cl_link_node* p = link->cl_link_head.next;
while(n)
{
if(condition(p, key) == CANFIND)
{
pthread_mutex_unlock(&(link->cl_link_mutex));
return p;
}
p = p->next;
n--;
}
pthread_mutex_unlock(&(link->cl_link_mutex));
return NULL;
}