正所谓“真传一句话,假传万卷书”。我觉得我们这一代是被教科书坑了的一代。教科书内容的各种反常识,反物理,反人类层出不穷。浅入深出的本事更是一本胜过一本。一般情况下,我只会打击一下文科类的科目,比如说语文、政治、历史什么的。那是因为我之前还比较单纯,觉得理科的事毕竟丁是丁、卯是卯,一般不会有什么大问题。然而,读过CSAPP后,如果不吐槽一下C语言教科书,我就对不起学弟学妹啊。不过具体到哪本C语言书,我就不说出来了。反正国内的教科书都是一大抄,不是吗?
关于补码
首先,我从百度百科上摘抄下对于补码的解释。这种解释与教科书上的极为相似,因此作为“教科书派”的代表:
正数的补码
正整数的补码与原码相同。
【例1】+9的补码是00001001。(备注:这个+9的补码是用8位2进制来表示的,补码表示方式很多,还有16位二进制补码表示形式,以及32位二进制补码表示形式,64位进制补码表示形式等。每一种补码表示形式都只能表示有限的数字。)
负数的补码
求负整数的补码,原码符号位不变,先将原码减去1,最后数值各位取反。(但由于2进制的特殊性,通常先使数值位各位取反,最后整个数加1。)
同一个数字在不同的补码表示形式中是不同的。比如-15的补码,在8位二进制中是11110001,然而在16位二进制补码表示中,就是1111111111110001。以下都使用8位2进制来表示。
【例2】求-5的补码。
因为给定数是负数,则符号位为“1”。
后七位:-5的原码(10000101)→符号位不变(10000101)→数值位取反(11111010)→加1(11111011)
所以-5的补码是11111011。
【例3】数0的补码表示是唯一的。
[+0]补=[+0]反=[+0]原=00000000
[ -0]补=11111111+1=00000000
好吧,我来梳理一下,“教科书派”描述的“补码”的写法,首先作了如下分类:
- 正数的补码与原码相同
- 负数的补码=(~原码+1)
- 0的补码表示是唯一的
其次,“教科书派”还说,位数不同,补码的表示形式也是不同的。
下面是“CSAPP”派的说辞:“教科书派”啊,你说的都对,你把表面现象都说出来了,可是你为什么不说补码的本质呢?你这样啰哩啰唆的,正数和负数不同,8位和16位不同。我说,正数和负数都一样,8位和16位也都一样!下面是“CSAPP”派的论述。
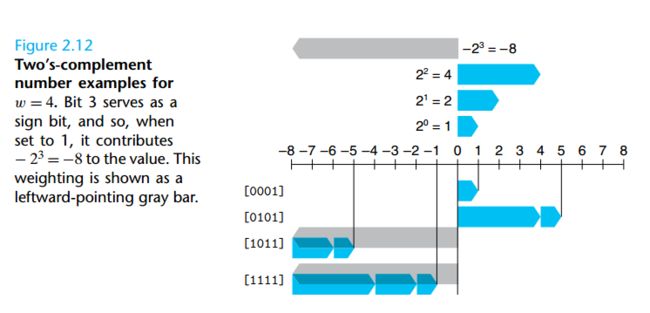
也就是说,除了最高位,其它位表示的意义都与原码一样。唯一的变化就是:原码的最高位作的是正贡献,而补码的最高位作的是负贡献。如果这样表述,正数跟负数不就是一样的?多少位又有什么关系?而且,比如告诉我用8位来表示一个有符号数,我马上就知道最大的负数是1000000(b),即十进制的-128。为什么?因为负贡献全开,而正贡献没有。而最大的正数是01111111(b),即十进制的127。为什么?因为没有负贡献,而正贡献火力开到最大。
最后加一句,补码是有符号数的一种表述方式,但不是唯一一种表示方式。但目前咱们接触到的编译器,基本都是用补码作为有符号数的编码方式的。
附上CSAPP上的一张例图:
关于对齐
面试的时候经常会考一种题型:
struct A{
int x;
char ch;
int y;
}A1;
问sizeof(A1)是多少。当时虽然闭着眼睛都知道是12。但是我一直以为,所谓的对齐是指ch的长度要凑到跟x的长度一致。鄙视自己!其实是怎么回事呢?下面摘录CSAPP的一段话:
许多计算机系统对基本数据类型合法地址做出了一些限制,要求某种类型对象的地址必须是某个值K(通常是2、4、8)的倍数。这种对齐限制简化了形成处理器和存储器系统之间接口的硬件设计。例如,假设一个处理器总是从存储器中取出8个字节,则地址必须为8的倍数。如果我们能保证将所有的double类型数据的地址对齐成8的倍数,那么就可以用一个存储器操作来读或者写值了。否则,我们可能需要执行两次存储器访问,因为对象可能被分放在两个8字节存储器块中。
无论是否数据对齐,IA32硬件都能正确工作。不过,Intel还是建议要对齐数据以提高存储器系统的性能。Linux沿用的对齐策略是,2字节数据类型(例如short)的地址必须是2的倍数,而较大的数据类型(例如int, int* float和double)的地址必须是4的倍数。注意,这个要求就意味着一个short类型对象的地址最低位必须等于0。类似的,任何int类型的对象或指针的地址的最低两位必须是0。
读完这两段,我表示秒懂。注意哦,这里的说法就不限于结构体内了。大家可以做个实验,看看你随便在哪里定义一些值,看short类型的最低位是不是为0?这里可以出一个思考题了:)
struct A{
int ai;
char bc;
short cs;
char dc;
};
请问ai,bc,cs,dc分别相对于结构体A的偏移是多少?结构体A的总大小是多少?