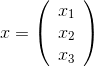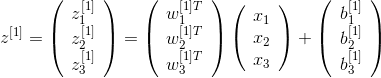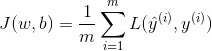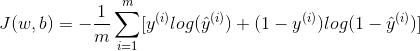学习资料:
网易云课堂:神经网络和深度学习(吴恩达)
知乎专栏:无痛的机器学习第一季
神经元与神经网络
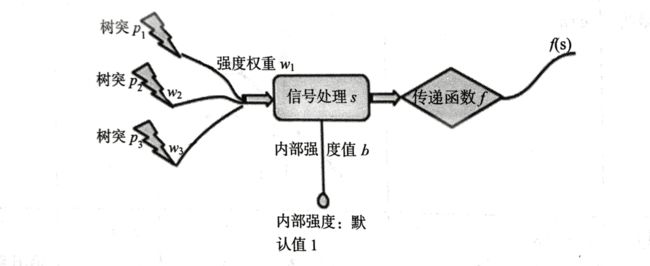
说到神经网络,我们第一个概念就是在高中生物学习到的神经元(neuro)的概念,神经元从树突接收到刺激信号,经过神经元的传导,再通过轴突将信号传递下去,我们将神经元的数据模型通过图片的形式展现出来:
类比于上述的神经元数据模型,下面我们给出一个最基本的神经网络(SNN):
在吴恩达的课程中,神经网络分为浅层神经网络和深层神经网络
一个神经元被称为logistic回归。
隐层(hidden layer)较少的被称为浅层,而隐层较多的被称为深层。
基本上是层次越深越好,但是带来的计算成本都会增加,有时候不知道个该用多少的时候,就从logistic回归开始,一层一层增加。
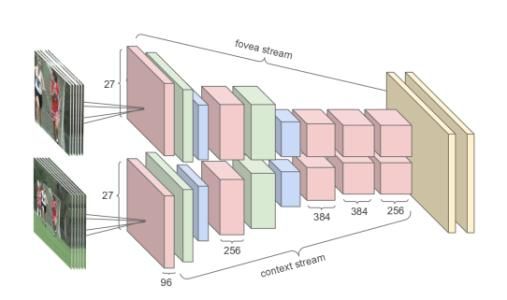
此外,神经网络还有卷积神经网络(CNN)与循环神经网络(RNN)。
刚才所说的只是大体上对神经网络的介绍,现在我们来研究一下神经网络具体模型。
神经网络的简单模型
上文说到一个神经元就是一个logistic回归,那我们先来介绍一下logistic回归:
logistic回归是一种广义上的线性回归,因此与多重线性回归分析有很多相同之处,它们的模型形式基本上相同,都具有z=w‘x+b。其中x是我们给出的数据,它可以是一个数,也可以是一个n维向量,w与b是我们的待求量。而logistic回归中通过函数L将z对应一个隐状态p,p =L(z),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数,就是logistic回归。
其中logistic回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释。
在了解了logistics回归之后我们来继续研究神经网络,我们采用的数据是二分类的,所以我们可以把它描述为(x,y),其中x是一个n维向量,y是0或1。
之后我们就要对输入信号进行处理,信号处理函数分为两部分,也就是logistic回归的处理方法
1.权重加权
对每个输入信号x1, x2, x3,乘以对应的权重分别为w1, w2, w3,然后加上内部强度 b
2.激活函数
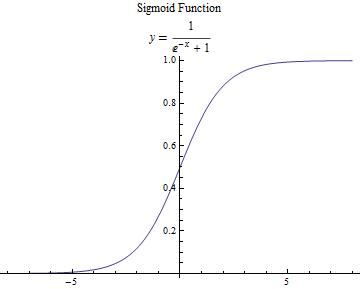
z可以取到R中任意值,不利于处理,所以我们需要进行处理数据,这就要用到激活函数 a=σ(z) 。一般来讲,我们经常采用sigmoid函数:
之前我们所说的是对单个神经元进行处理,一个神经元不可能只处理一组数据,而且神经网络不可能只包含一个神经元,所以我们扩大我们的样本数量:
其中每个xn都是n维的向量,y属于{0,1}。
对第一层神经元而言,第一步计算z:
简化一下,就是
第二步计算a:
抽象一下,第 l-1 层输出到第 l 层的公式就是:
注意这里,用 a[l-1]替代了 x,因为,实际上而言a[0]就是输入层x。
以上就是基本神经网络的简单模型,之后我们会介绍一下神经网络的训练。
神经网络的训练
对于神经网络来说,我们不可能在一开始就给出神经网络的最优解,所以我们需要足够的样本来训练它。
简单总结一下,对于单个神经元来说,其logistic回归为:
其中ŷ为我们计算的输出标签,实际上它会与实际值y有所偏差,所以我们需要引入函数来计算偏差的大小:
LOSS FUNCTION(损失函数):
一般来说,我们高数课上讲的比较ŷ与y的函数是:
可是上述函数的缺点为它会给出很多局部数据的最优解,在我们绘图是它会出现类似波浪形状的图形,在整体上会有很多点是非凸的,无法用梯度下降法找到最优解,于是我们引入如下函数:
在这个公式中,当ŷ越接近于y时,这个函数的值就越小,也就说明我们的神经网络越好。我们简单地代入两个极限值0和1来证明这个函数的正确性。
1.如果 y=1,则 L(ŷ, y)=-log(ŷ),只有当ŷ趋近于最大值1时,-log(ŷ) 才达到最小
2.如果 y=0,则 L(ŷ, y)=-log(1-ŷ),只有当 ŷ 趋近于最小值0时,-log(1-ŷ) 才达到最小
损失函数只是针对单个样本数据的,当我们面对m个样本时,我们就要引入成本函数。
COST FUNCTION(成本函数):
很简单,对多个损失函数的解计算其数学期望(求平均值)
展开函数得:
很明显,成本函数越小,证明我们的训练效果越好,那我们如何减小成本函数呢,之后我们会介绍梯度下降法。
梯度下降法
我们都知道,对于一个多元函数来说,梯度即是某一点最大的方向导数,沿梯度方向函数有最大的变化率(正向增加,逆向减少)。(∂u/∂L)M0=n∗l=|n|cosθ当θ=0时,该方向为函数的梯度方向,梯度表示为:
所以在我们求出成本函数值后,我们要对w进行修正,我们对损失函数L(ŷ,y)取一个截面,假设我们在现有的数据在A点
其中,无论是在最小值的左右,每进行一次迭代都会是w点向最小值靠近,只要训练样本足够多,我们就会找出一个成本函数在预期范围内的神经网络。