采用步步逼近的方式构造问题的解,其下一步的选择总是在当前看来收效最快和效果最明显的那个。
使用前提: 验证贪心模式的有效性
最小生成树(minimum spanning tree)
输入:无向图G=(V, E); 边权重w(e)
输出:树T=(V, E'),
其中, 使得权重 = \sum_{e \in E'} w_e)
树的性质
- 具有n个节点的树的边数为n-1
- 一个无向图是树,当且仅当任意两个节点间仅存在唯一路径
Kruskal算法
不断地重复地选择未被选中的边中权重最轻而且不会形成环的一条。
procudure kruskal
for all u in V:
makeset(u)
sort the edges E by weight
for all edges {u, v} in E, in increasing order of weight:
if find(u) != find(v)
add edge {u,v} to X
union(u, v)
- makeset(x): 创建一个仅包含x的独立集合
- find(x): x属于哪个集合?
- union(x, y): 合并包含x和y的集合
共需要|V|次makeset + 2|E|次find + |V|-1次union操作
find操作不一定成功触发union操作,因此最坏情况下会需要2|E|次
数据结构:有向树
集合中的顶点对应树的节点,每个节点包含一个父指针,一级级指向树根。树根的父指针指向该元素自身。
node
- p //父节点指针
- rank //该节点下悬挂的子树高度
- 方案一
合并时让较低的树的根指向较高的树的根(基于等级的合并)
procedure makeset(x)
p(x) = x
rank(x) = 0
procedure find(x)
while(x != p(x))
x = p(x)
return x
procedure union(x, y)
rx = find(x), ry = find(y)
if rx == ry return
if rank(rx) > rank(ry)
p(ry) = rx
else if rank(rx) == rank(ry)
p(rx) = ry
rank(ry) += 1
else
p(rx) = ry
- 方案二
路径压缩: 循着一系列的父指针最终找到树根后,改变所有这些父指针的目标,使其直接指向树根
procedure find(x)
while(x != p(x))
p(x) = find(p(x))
return x
find中rank未进行更新,此时rank的含义无法解释为子树的高度。
此时有向树的高度不会超过2。
- 方案三
我们可以发现find和union操作均只关心树的顶层,是否可以直接使用树高为2的有向树呢?并在union()操作中,对于两个树高为2的有向树,进行其中一棵的压缩。
但仔细分析可以得出,此方案与方案二本质相同,仅将find()操作总共所做的工作转移到union()操作中。
| 方案序号 | makeset | find | union | 该部分效率 |
|---|---|---|---|---|
| 1 | O(1) | O(logn) | O(logn) | (V+E)logn |
| 2 | O(1) | > O(1) | > O(1) | V+E |
方案2如何平摊分析?TODO
总时间复杂度为T(sort)和T(find/union)中较大的那个
see java implement: greedy.mst.KruskalMST
Prim算法
算法中间阶段的边集X构成一个子树,该子树顶点的集合表示为S。我们选择S中顶点与S外顶点之间的最轻边加入X,即以最小代价将所有原本不属于S的顶点包含进来。
与Dijkstra的关系
伪代码基本一致,区别体现在优先队列排序使用的键值
- Prim: 键值为节点与集合S中顶点间的最轻边的权重;
- Dijkstra:键值为节点到起始点的完整路径长度;
pseudocode如下:
procedure prim
for all u in V
dist(u) = \infty
pre(u) = nil
dist(s) = 0
PQ = makequeue(V) (using dist-values as keys)
while PQ is not empty
u = deletemin(PQ)
for all edges (u, v) in E
if dist(v) > l(u, v)
dist(v) = l(u, v)
pre(v) = u
decreasekey(PQ, v)
可以看到仅是dist(u)+l(u, v)变为l(u, v)
see java implement: greedy.mst.PrimMST
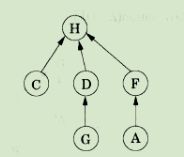
哈夫曼编码
- 编码压缩
压缩比越高,随机性越低,可预测性越好
- 无前缀特性,任一个码字都不应该是其他码字的前缀
无前缀编码中每个字符对应于树中的一个叶节点
procedure Huffman(f)
Input: An array f[1...n] of frequencies
Output: An encoding tree with n leaves
let H be a priority queue of integers, ordered by f
for i = 1 to n: insert(H, i)
for k = n + 1 to 2n -1
i = deletemin(H), j = deletemin(H)
create a node numbered k with children i,j
f[k] = f[i] + f[j]
insert(H, k)
编码输出
call print(root, 1)
print(node, num) {
if node is null return
print node's code based on num
:num to binary and then remove the head '1'
print(node.left, 2*num)
print(node.right, 2*num + 1)
}
see implement: greedy.Huffman
其他
Horn公式
问题描述
Horn公式中最基本的对象是取值为true或false的布尔变量,变量的知识通过蕴涵式、纯否定两类子句来表达。给定某个由以上两类子句构成的集合,我们需要判断是否存在一个一致的解释,即一组使得所有子句都满足的变量(true/false)赋值,该解释成为该Horn公式的一个可满足赋值。
求解策略
从所有变量为false开始,依次将“只需且不得不”这样做以使得某个蕴涵式满足的变量置为true;一旦所有的蕴涵式都得到满足,再回头检查是否所有否定子句仍然满足。
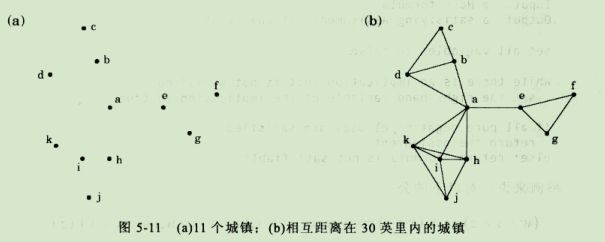
集合覆盖
问题描述
图中的点表示一组城镇,需要建设一些新的学校。
具体要求:
- 所有的学校都必须建在城镇上
- 从任意一个城镇触发,都应该可以在30英里的范围到达其中的某一所学校
那么,最少需要建多少所学校呢?
较优解求解策略(贪心)
对每个城镇x,令S(x)为在其30英里范围内的城镇集合。
选取包含未被覆盖元素的最大集合Si,不断重复,直到所有元素都被覆盖。
贪心算法的逼近因子
贪心算法的解与实际的最优解的规模之比可能因问题输入的不同而不同,但是总小于ln(n)。我们称这一最大比值为贪心算法的逼近因子。
写在最后
- 立个Flag,
TODOwill be done some day。 - 渣代码,且轻喷:worried:。