介绍
使用到的数据集是lossalae数据集，包含了1500个liability claims.
数据如下：
> head(lossalae)
Loss ALAE
1 10 3806
2 24 5658
3 45 321
4 51 305
5 60 758
6 74 8768
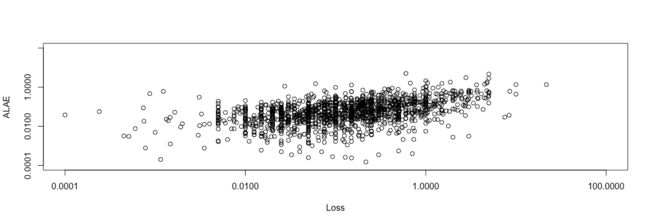
对数据进行可视化：
nn <- nrow(lossalae)
loss <- lossalae/1e+05;
lts <- c(1e-04, 100)
plot(loss, log = "xy", xlim = lts, ylim = lts)
image.png
Componentwise Maxima
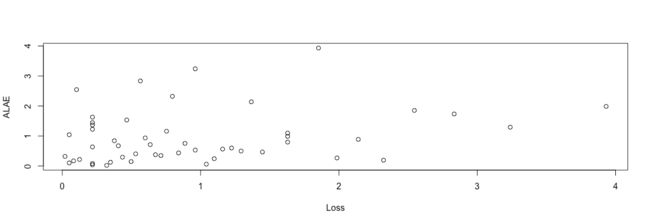
出于演示目的，我们使用第1节中介绍的数据通过随机取k = 50个大小为m = 30的组来创建分量块最大值的数据集，从而产生在m个观察值3上取得的k分量最大值3。 双变量极值分布通常用于模拟这种类型的数据。 下面的代码创建了分量最大值数据cml并生成两个数据图，第一个显示原始数据和分量最大值，第二个显示组件最大值数据转换为标准指数边距。
set.seed(131); cml <- loss[sample(nn),]
xx <- rep(1:50, each = 30); lts <- c(1e-04, 100)
cml <- cbind(tapply(cml[,1], xx, max), tapply(cml[,2], xx, max))
colnames(cml) <- colnames(loss)
plot(loss, log = "xy", xlim = lts, ylim = lts, col = "grey")
points(cml)
ecml <- -log(apply(cml,2,rank)/51)
plot(ecml)
image.png
image.png
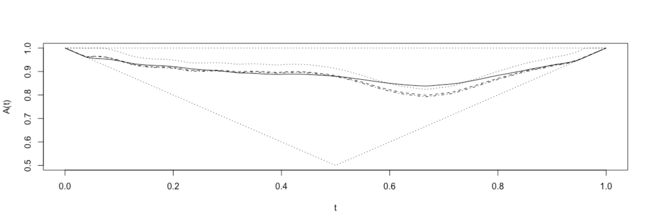
以下代码从分量最大值数据估计并绘制依赖函数A（·）。 第一代码块使用依赖函数的各种非参数估计，并且还使用由epmar = TRUE指定的边缘的经验（即非参数）估计。 四种不同的估计如图3所示。第二种代码块使用参数模型的最大似然估计。 对fbvevd的调用适合模型，对绘图的调用绘制了参数依赖函数估计。 在第一次调用fbvevd时，参数规范asy1 = 1约束模型拟合，以便模型的第一个不对称参数固定为值1。
pp <- "pickands"; cc <- "cfg"
abvnonpar(data = cml, epmar = TRUE, method = pp, plot = TRUE, lty = 3)
abvnonpar(data = cml, epmar = TRUE, method = pp, add = TRUE, madj = 1, lty = 2)
abvnonpar(data = cml, epmar = TRUE, method = pp, add = TRUE, madj = 2, lty = 4)
abvnonpar(data = cml, epmar = TRUE, method = cc, add = TRUE, lty = 1)
m1 <- fbvevd(cml, asy1 = 1, model = "alog")
m2 <- fbvevd(cml, model = "log")
m3 <- fbvevd(cml, model = "bilog")
plot(m1, which = 4, nplty = 3)
plot(m2, which = 4, nplty = 3, lty = 2, add = TRUE)
plot(m3, which = 4, nplty = 3, lty = 4, add = TRUE)
image.png
image.png
fbvevd生成的对象包含有关二元极值分布的参数拟合的信息。 例如，m2包含关于（对称）逻辑极值分布的拟合的信息，其具有单个依赖性参数和每个GEV边缘上的三个参数。 使用图（m2）产生几个诊断图，包括分位数曲线和光谱密度。 使用偏差（m2）产生偏差，该偏差等于负对数似然的两倍。 下面显示了参数估计值及其标准误差，并给出了测试m2与m3的偏差表的分析，这是可能的，因为模型是嵌套的，m3具有一个附加的依赖参数。 在Tawn（1988）之后，对exind.test的调用产生了独立性的分数测试。 省略方法参数给出了似然比检验，也来自Tawn（1988），这通常更准确。