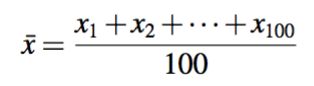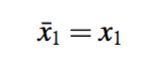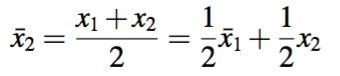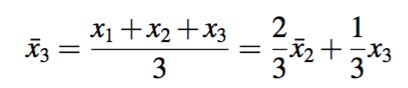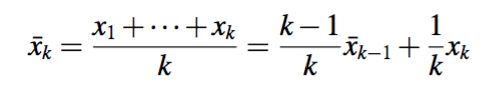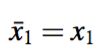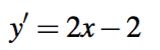我们在前一篇提到了在线贝叶斯估计,在这一章中,我们讲述在线贝叶斯估计体现出来的重要思想:要精益求精,不要步步为营。
在线贝叶斯估计与在线算法
我们在前一章中第一次提到了 在线贝叶斯估计 的概念:当证据源源不断到来时,贝叶斯估计并不是等着所有的所有的证据来了以后才开始计算基于所有收集到的观测的后验概率。而是开始根据少量的证据计算一个概率,然后每次拿到每一个新观测的时候,都用该观测来调整之前的估计。
以开水房打水的例子而言,你进入开水房准备打开水,你想知道这个水是否开了,在这个过程中,你实际上是一步一步拿到证据,并且用这些证据不断更新你上一步的猜测的:
- 在你还未看到烧开水的机器之前,根据你过去的经验,你得到一个水开的先验概率: P0=P(水开)。
- 然后,你会先观察一下开水器的电源灯是否亮起,根据这个观测在 P0 的基础上提高或者调低水开的概率,得到 P1= P(水开|电源灯状态)。
- 其次,你在灌水的初始,会观察水是否冒热气,并根据这个观测在 P1 的基础上来调整水开的概率:得到 P2= P(水开}|电源灯状态,热气)。
- 最后灌水之后,你会隔着杯子感受这个温度,并将这个观测加入到之前的证据中对P2 做更新,得到 P3= P(水开|电源灯状态,热气,温度)。
这个例子中,观测是源源不断来的。在线贝叶斯估计使得我们不用等拿到所有可能的观测之后再估计一个最终的后验概率,而是可以
- 每次来一个观测,我们都用该观测,对前一次计算的后验概率进行更新,得到一个新的后验概率。
- 并且,在上一步的基础上更新的后验概率,和用所有观测重新计算得到的后验概率完全一样。
贝叶斯的在线估计算法的核心,和很多在线算法(on-line algorithms) 相同。在线算法的核心步骤包括以下几点:
- 在最初时刻,根据最初的一个或者几个数据得到一个初步结果。
- 每次来一个数据,用这个数据更新上一次的结果。
- 这个更新的结果,和用此时之前的所有数据得到的结果一致。
和在线算法相对的叫做离线算法(off-line algorithm)。离线算法又被称为batch algorithm。离线算法对于新来的数据,总是把它加到前面的数据重新计算得到结果。比如说一开始你有100个数据,你用这一批数据得到了一个结果,当你又有了100个新的数据后,你需要把这100个和原来的100数据合并起来,用200个数据重新计算一下结果。这就是离线算法。
在线算法和离线算法的最大的不同是不需要重新计算,而是在前一次的计算的结果上进行调整:拿到新的100个数据之前,用着100个数据来更新之前计算的结果,更新的结果和用200个数据重新计算的结果一样。因此在线算法和离线算法最大的差别不在于数据是否一个一个来,而在于是需要重新算,还是在原来的基础上进行更新。
在线算法的例子:求均值
我们用求均值的例子来说明在线算法和离线算法的区别。假若给你100个数,从x1,x2,...,x100,要求它们的均值很容易:
这种方法是拿到所有的100个x后一起计算的。这就是离线算法。
而在线算法是如何计算的呢?
- 在k=1时刻,我们拿到 x1,此时我们计算一个均值
这个均值,是基于当前的所有数据(只有一个x1)计算得到的。
- 在k=2时刻,我们拿到 x2,我们需要在上一时刻的均值的基础之上,用新的数据x2进行调整,并且使得调整的结果和 x_1、x_2这两个的均值相等。我们很容易找到如下形式:
- 在k=3时刻,我们拿到 x3,此时的均值也可写成用 x3 来更新上一时刻的均值的形式:
- 以此类推,可以看出在任意k时刻,当我们拿到 xk 时,此时的均值写成在用 xk 来更新前一时刻(k-1时刻) 的均值的形式:
也就是说,从初始估计
出发,
这个就是求均值的在线算法。
相比离线算法,在线算法有三个巨大的优势:
- 即时反馈:不需要等到所有数据来了之后才能知道结果,任何时刻都会存在一个结果。并且这个结果,是基于迄今为止拿到的所有数据基础之上的最优结果。
- 计算量小:来了新的数据后,不需要重新计算,而只需要在上一步计算的结果上进行更新即可,大大的节省了计算量。
- 存储量小:不需要存储原始数据,每次只需要存储上一次的结果即可,大大节省了存储空间。
不仅如此,在线贝叶斯,乃至所有的在线算法体现出来的一种思想,就是精益求精:在最开始,我们并不求完美,而是先得到一个结果;我们在该结果的基础之上,不断的接收新的信息对原来的结果进行改进,以达到我们所追求的最优的目标。
精益求精的例子
精益求精的这种思想,在很多领域都有非常多的体现。举几个例子。
例子1: 函数极值的数值解法
在我们高中的时候,我们就学会求一个函数的最大值或者最小值。我记得最常用的方法就是求导法。我们将函数的表达式求导数,令其为0,建立一个方程。方程的解就是这个函数的极值。
例如对于函数
而言,该函数的导数为
令导数为0,即
因此 x=1 就是使得该函数有极值的自变量的值。这种方法得到的自变量的值,叫做该问题的 解析解(analytical solution)。本质就是根据公式严格进行一步一步地推导,最后得出最优解的表达式。 解析解的一个问题是, 很多函数的导数形式十分复杂,甚至在很多位置上不存在。因此函数极值的数值解法应运而生。
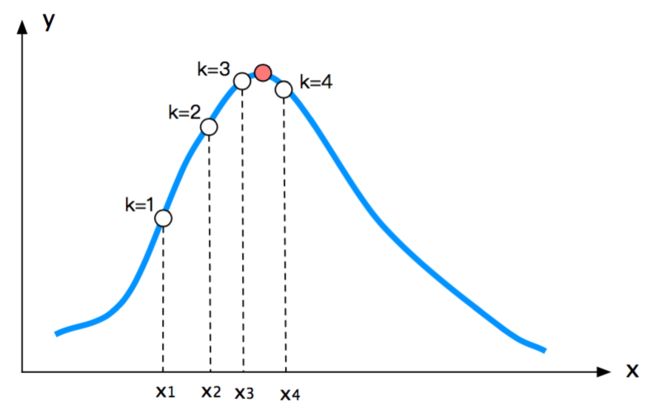
与解析解相对的,就是数值解(numerical solution)。数值解的核心思想就是精益求精。我们用下图来解释。图中的蓝色曲线,就是这个函数y的表达式。我们想找到这个函数最大值对应的x的位置(红点处)。
找到数值解具体有以下几步:
- 第一步(k=1):随便猜一个x值。你没看错,就是随便猜。假设我猜的位置为 x1,显示在图中。显然这么随便猜一个值,几乎不可能是最优解。不是最优解没关系,当我们猜到
x1 这个位置以后,我们计算一下在 x1 这个位置附近,该函数是上升的还是下降的。这个可以用函数的梯度来得到。本例子中 x1 的附近该函数是上升的。这个意味着,我们如果增大
x1,我们就可以得到一个更大的y。 - 第二步(k=2): 于是,我们在 x1 的基础上增加一点,假设达到 x2 的位置。同样,我们看一下该函数在 x2 的附近是上升还是下降。这个例子中仍然是上升。我们还应该继续增加 x。
- 第三步(k=3):,因此我们在 x2 的基础上,再次增加一点,达到 x3。按照上述的方法判断依然应该增加。
- 第四步(k=4):,我们在 x3的基础上,再次增加一点,达到 x4,则这时候,我们发现函数在 x4 的周围是下降的,这意味着我们应该往回退一点。
- 不断重复上面的步骤,经过多次,可能逼近最优的红点位置。
我们可以发现,找到数值解的思路是并不试图一次就找到函数最优值的位置,而是用逐步迭代的方法不断逼近最优值。这就是精益求精的思想。
而我们刚才的解析解的方法,是根据公式严格推导。这种方法用成语步步为营来描述最为贴切。相比较于精益求精,步步为营有两个缺点:(1)知道最后一步之前,你永远不知道答案,哪怕是一个粗略的答案(2)一旦任何一步出了错误,最后的结果都是错的。
从这一点来说,我们在初高中的最后几道大题都是步步为营:在你推出最后结果之前,你不知道你证明对了还是错了,并且一旦中间任何一步错了,你都无法得到正确的结果。
例子2: 项目管理中的敏捷模型
熟悉项目管理的人,都知道项目管理有两种不同的模型。第一个模型是瀑布模型(Waterfall model)。瀑布模型将一个系统的开发分成包括需求分析、设计、实现、发布等多个阶段。每个阶段都有相应的管理与控制,因此能够比较有效的确保系统品质。瀑布模型显示在下图中的上半部分。我们可以看出,瀑布模型中各个阶段有相互衔接的固定次序,如同瀑布流水,逐级下落。
然而,用瀑布模型来进行项目的管理有2个重要的缺点:
- 不适应用户需求的变化。因为用户需求在最前端,一旦用户需求发生变化,则整个开发过程全部需要从头再来。
- 只有在项目生命周期的后期才能看到结果。
与瀑布模型相对的是敏捷模型(Agile Model)。敏捷模型显示在上图的下半部分。我们可以看出,在用敏捷模型来开发项目中,整个开发工作被组织为一系列短周期的快速迭代。每一次迭代都包括了需求分析、设计、实现与测试工作,并通过客户的反馈来进行不断改进,直到达到最后的要求。
和瀑布模型相比,用敏捷模型来进行开发的突出优势在于
- 敏捷模型的短周期迭代的思想,可以很好的适应用户需求的变化。
- 能够最快的得到早期用户反馈,进而可以在没有考虑到的情况下进行快速改进
这里说的瀑布模型和敏捷模型,同我们刚才的函数极值的解析解和数值解何其相似!瀑布模型和解析解这两种方法,都是采用了'步步为营'的思路,而敏捷模型和数值解,就对应着`精益求精'的思路。
例子3:最简可行产品
很多年前,我和同事一起去和一家私营公司的CEO谈项目合作。这个公司是做国内做高压电线自动检测最好的一个公司。简单的来说,他们做了一个设备,可以用一根长的杆子捅到高压电线上挂住,然后实时检测输电线路是否正常工作。一天晚饭的时候,这个CEO在和我谈到他们开发的思路的时候,说了这么一段话:
像我们这样的小公司开发产品,尤其是科技含量较高的产品,不能想着一步到位。最开始,一定要把一个不完美,但可用的产品搞出来。这样我们心里就有底了。然后拿到现场去用,工程师在部署后会告诉我们很多设计之初没想到的问题,用户会给我们提供更多的要求,我们就在这些基础上一步一步改进。别看我们现在这个产品功能看着这么漂亮,但是第一代产品刚出来的时候问题非常多。
这么多年,我仍然记得清清楚楚他说的这个就是不完美,但可用的产品的这个概念。后来我才知道,这就是大家所说的`最简可行产品'(minimum viable product,简称 MVP)。MVP的严格说法,是指的有部分机能恰好可以让设计者表达其核心设计概念的产品。设计者可以进行验证式学习,根据使用者的回馈,进一步了解使用情形,并且继续开发此产品。
我在香港的胡子科技学院(http://mtache.com/mvp/)的网页上看到下面一个例子。
一个人想去创业,做一个关于足球的社交平台,可以让人在该平台上组队 订场去踢球。
他很快找到了另一个IT拍挡, 一起进行这个项目。他们非常认真,并放弃了一些其他的
工作机会,全心全意投入这项目。
他们这个团队对该平台要求非常高。他和开发团队慢慢地打磨该产品,开发一些特别的功
能,例如要在平台上drag & drop人到球场上组队。这些功能开发起来都非常费时,开
发进度比预期慢。但他们认为这是必须的,因为要确保能够推出一个`完美'的产品到市
场。
一年后,这个`完美'的产品终于完成,准备要推出市场。然而,当他们把产品推出到市场
后,却发现:没有人用!
没有人用的原因,可能是推广不足,也可能是市场并没有这个需求!最后,整个项目不了
了之。
市场的反应往往是难以预料的。尤其是初创企业。试想想当你投放了大量资源、金钱、时间,请了一队团队去开发一个 APP/平台,推出到市场后却发现没啥人用,感觉是绝对不好受的。
解决这个'推出市场后没有人用的问题'最好方法,就是MVP。创业者与其花大量资源去开发一个自以为会成功的完美产品,倒不如用最快的方法,建立一个只有最少、最基本功能的'半成品'。先把这个'半成品'推到市场,看看市场的反应。
有很多非常成功的初创企业,也是遵循MVP的精神。Groupon这家市值上亿美元的公司,便是MVP的一个很好例子。
创办人Andrew Mason 在成立Groupon初期,与其花资源去建立一个`完美的团购系统',他只建立了一个简单的WordPress博客。这个博客定时会放上一些商店优惠的文章,而其优惠也只是透过人手,一封一封的去电邮给参加者!后来,他发现这个发布商店优惠文章的博客非常受欢迎,Andrew 因此确定这个主意有市场后,才开始组织团队去开发这个团购系统。
上一个例子中的敏捷模型,其实就是先力争推出一个MVP。推出MVP之后,开发者可以根据用户或者使用者的回馈,进一步了解使用情形,并且持续不断的在上一个版本的基础上,根据实际情况进行改进。
MVP和刚才说的敏捷模型,实际上还和最近互联网行业推出产品基本的做法小步快跑,快速迭代的思路完全一致。
小步快跑,快速迭代,就是不要想着一次性发出好的产品,而要通过快速迭代的方式进行更新,保证每一小步都跑得很快。在快速迭代理念支持下的产品研发是'上线-反馈-修改-上线' 这样反复更新内容的过程。再开始时,要允许不完美,但要通过快速迭代逐渐向完美逼近。每天都能发现修正一两个小问题,不到一年产品就打磨出来了。
与之相对的,如果开始总是面面俱到的谋布局,并且在每一步尽善尽美求完美否则不肯往下走,这样的问题就在于,你开始一旦某一个点没考虑到或者考虑不周全,那么你只能到最后一步才会发现问题所在,此时重头再来的代价和时间成本会过于昂贵。
凯文•凯利在他的畅销书《失控》里,有过这么一段话:
由此说到机器,有一个违反直觉但却很明确的规则:复杂的机器必定是逐步地、而且往往
是间接地完善的。别指望通过一次华丽的组装就能完成整个功能系统。你必须首先制作一
个可运行的系统,作为你真正想完成的系统的工作平台。...在组装复杂机械过程中,收益
递增是通过多次不断的尝试才获得的-也即人们常说的'成长'过程。
例子4: 用精益求精的方法来写论文
我在香港理工大学期间,听到过一位我非常敬佩的老师来组里给学生分享过应该如何写学术论文。
他告诉我们,写一篇论文有两种方案。第一种方案,是迟迟不下笔,要等着把idea想好,仿真做好,实验完成之后,拿到了所有的素材之后才开始写。在写的过程中,按照自然顺序一章一章的打磨,写完一章,再写下一章。
第二种方案,就是稍微有了一个idea就开始写,甚至这个idea都不需要很好。写的过程中,不打磨语法,用最快的时间写出一个初稿。初稿写完以后,给周围的人看,让他们提意见,这时我们就会知道这个文章的idea有哪些漏洞,如何改进等等。然后不断的进行多次`快速迭代'式的修改文章。每次修改,都完善idea,仿真、实验,修改语法,这样最终把文章打磨完成。
这位老师说,我们一定要用第二种方法来写文章。
现在看起来,确实应该如此。如果按照第一种方案来写文章,你可能永远都写不出一篇论文。原因在于,(1) 只有当你写完以后,别人才可能给你意见,一旦你发现某一个意见可以采纳,你可能需要重新做实验,做仿真,又重头来过,导致时间耗费的过长。(2) 写文章的过程中,如果按照一章一章的仔细打磨,你可能发现你写到后面的时候,因为需要修改idea或者仿真等,前面的部分很多需要重新写,这些仔细打磨的部分就全部浪费掉了。
其实,不仅仅是写科学论文,我觉得这种方式可以用到写任何文章的方法。Facebook人工智能研究院智能围棋项目的负责人,也是网上的著名科学段子手田渊栋,在他的知乎专栏中发表的一篇文章《碎片化时代如何读写》中,写到下面的一段话:
我的经验是先把自己想说的零碎思路写下来,然后反复看反复组织,才能写出长文来。在
第一阶段写零碎思路时,往往先有个模糊的提纲(这也是写作的第一推动力),然后无拘
无束地写,这样九成会离题万里,说些自己潜意识里想说,但却和初衷完全违背的话来。
但这完全没有关系,只要咬住一个字“快”,十几分钟就有大段稿子。我有时候程序写到一
半,突然有个想法想写下来,那就切到另一个窗口开始打字,等榨干了自己的想法,再回
去写程序,这样至少可以保存思考的火种,之后可以继续。
这样写出来的文章,大多是不忍卒读兼无人可懂的。这样就跳到第二阶段。视情况一般有
两种选择,可以根据内容修改主题,或者受已经写下的片断启发,重新写些与主题相关的
句子。这时候选择切题的段落,打通全文脉络是最重要的,能否成文取决于此,如果看到
一个有开头结尾的完整故事,那就算局部不通顺或者详略失当,这一篇文章也是板上钉钉
有了。
这种方式,实际上就是先尽可能写出一个MVP出来,然后再不断迭代去改进。从这个意义上来讲,最初迅速的完成一个MVP,比花很长时间完美的完成一个产品要重要的多,这也是印证了这句格言:
完成比完美更重要 (Done is better than perfect)。
用精益求精的方法的好处
我们在前面几个例子中,说到了用精益求精的思想来开发产品、写文章等的好处。你应该可以理解,用精益求精的思想的好处在于,可以快速后端的用户(或者开发者本身)得到反馈,迅速完成迭代升级。
其实,从开发者是否能完成这个项目而言,用精益求精的思想来做项目,有两个好处。
第一个好处,是安心! 在前面的'例子3:最简可行产品'中,那个CEO和我说的一段话中就可以反映这一点:最开始,一定要把一个不完美,但可用的产品搞出来。这样我们心里就有底了。
心里有底,这就是安心。起码从方案上来讲,这个方案是可行的。开发者需要做的,就是在这个可行的方案上进行改进而已。即便哪一点改进不成功,退回原来的版本即可,起码这个版本可以work!相反的,如果用步步为营的方式来做项目,直到你到达最后一步之前,你都不知道这个产品到底能不能工作,压力山大!一旦不能工作,你可能需要重头再来。这就是精益求精比步步为营的好处。
第二个好处,就是多次的即时反馈。开发者用精益求精的方式改进MVP,每次改进成功,实际上都可以获得完成时的成就感。一旦得到这个成就感,开发者又可以迫不及待地投入了下一个小目标,进一步改进当前的版本。
我在上课的时候问过我的学生一个问题,为什么一个人上自习学习的时候,坚持1个小时不到可能就得休息,而玩游戏的时候,则可以通宵呢?
原因就在于学习的反馈链条很长,而玩游戏可以得到即时反馈。
《游戏改变世界》一书中,揭示了人类会被游戏吸引的深层机理就是:即时反馈。游戏开发人员深谙此道。你在游戏中的任何操作,都会立马视觉化、数据化地显示出来。
不要小看每次砍怪物头上飚出的数字,不要小看出招的音效,不要小看伤血的红字和加魔的蓝字,它们都给玩家提供了最最直观的即时反馈。
你清楚的知道,你这次击杀怪物,一定会涨经验值,并且有几率会得到一些宝物。其实就是说,及时反馈使得你明确知道,你的每一次操作,都是有回报的,并且回报就在操作完成时!这就是使得我们能通宵玩游戏的原因。
对比现实生活中的学习却相反。今天你费劲心力背了50个单词,几乎完全不能立刻看出你付出努力的成效:之前看不懂英文书还是看不懂,之前听不懂的英文电台还是听不明白。你只有持之以恒的坚持很多年,才会突然有一天发现你的英语水平涨了。但是这个反馈链条未免也太长了吧。
包括英语的很多学科、乃至很多技能的学习的反馈链条都很长。例如小提琴和二胡。直到你付出非常长时间的枯燥的练习之后,你拉出的声音才不至于让人立刻想把你赶走。自己的努力不能得到即时反馈,就是很多人不能静心下来学习的主要原因。
忍不住想起了左小祖咒唱的这个《交作业》的这首歌
凭什么要我交作业?
交了,又不一定是自己写的!
写了,又定不一定考!
考了,又不一定能毕业!
毕了业,又不一定找到工作!
找到工作,又不一定找得到老婆!
娶了老婆,又不一定会生孩子!
生了孩子,又不一定会用功读书!
会用功读书,又不一定考得上!
考得上,又不一定交作业!
天哪,这个反馈链条如此之长,并且回报充满了如此之多的不确定性,难怪没有动力交作业啊。。。。
怎么破?其实核心就在于如何缩短这个反馈链条。例如背单词的时候,你可以引入奖励机制或者自我成就机制,例如每次完成50个单词的任务,就给自己一个奖励,或者在你的完成任务列表上重重的打一个勾!
从另外一个角度而言,我们需要训练自己的延迟满足的能力。延迟满足,就是一种克服当前的困难以获得长远利益的能力。 通俗地说,就是坚韧(Grit)。坚韧不拔的忍耐能力,对一个人极其重要。
本章总结
我们今天的收获是:
- 在线贝叶斯,乃至所有的在线算法体现出来的一种思想就是精益求精。
- 精益求精的这种思想,在包括函数极值的数值解法、项目管理中的敏捷模型、最简可行产品、以及写文章中都有体现。
- 精益求精,和每一步力求完美的步步为营相比,具有适应变化能力强、能及时得到外界反馈、让开发者安心、以及给开发者创造即时反馈的诸多优点。