Description
Given a set of candidtate numbers candidates and a target number target. Find all unique combinations in candidates where the numbers sums to target.
The same repeated number may be chosen from candidates unlimited number of times.
All numbers (including target) will be positive integers.
Numbers in a combination a1, a2, … , ak must be in non-descending order. (ie, a1 ≤ a2 ≤ … ≤ ak)
Different combinations can be in any order.
The solution set must not contain duplicate combinations.
Example
Example 1:
Input: candidates = [2, 3, 6, 7], target = 7
Output: [[7], [2, 2, 3]]
Example 2:
Input: candidates = [1], target = 3
Output: [[1, 1, 1]]
思路:
最开始想的是每一次将所有元素都全部遍历一遍,如[2, 3, 3]会从[]开始到[2] [2] [3],第二个[2]因为与第一个[2]相等,加一个判断去掉,变成[2], [3],然后再变成[2,2], [2,3], [3,3],每一次添加新元素都从头开始遍历,如果添加的新元素小于combination的最后一位则跳过,添加的新元素加起来combination大于target就返回不再继续往下返回, 如果相等就存储到results里后返回。
这种思路有许多地方可以优化,第一因为数字可以重复使用,所以一个2与两个2并没有区别, 可以直接用一个set将原来的candidates的重复元素去掉,然后在升序排列成新的candidates,这样就不需要在后面判断重复元素。第二添加的新元素必然大于等于combination的最后一位,所以可以将index作为输入变量,这样不需要每次都从头遍历, 第三每次都求和的行为可以变成用target将之前combination的和减掉得到新的target来替换,这样只要比较新的target与新加入元素的大小就可以决定是否结束搜索。
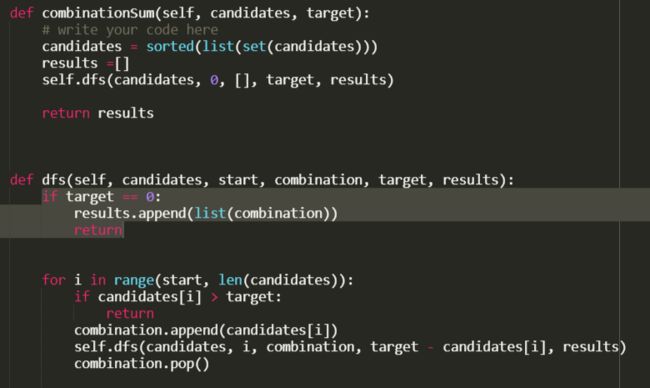
代码: