前几日宝刀君推送了一篇自动控制原理求传递函数的文章:见路不走!抛去结构图变换,放弃画信号流图,梅逊公式毅然肩负起了求传递函数的使命!在文中,宝刀君不惜用大量的图片来解释梅逊公式,并曾扬言理解了梅逊公示后,就可以自由的驰骋在经典自控的各个章节中!
或许有同学对此嗤之以鼻,有这么厉害吗,你一个小小的梅逊公式能掀起多大的浪花?
嘿,你还真别不信,今天宝刀君就将梅逊公式请出来,看看戎马一生的他,是如何在经典自控的各个章节中大显身手、是如何携手好搭档闭环特征方程巧妙解决各章典型问题的!
换句话说,今天的文章就是在向你解释:为什么宝刀君称梅逊公式和闭环特征方程是自动控制原理的解题精髓?
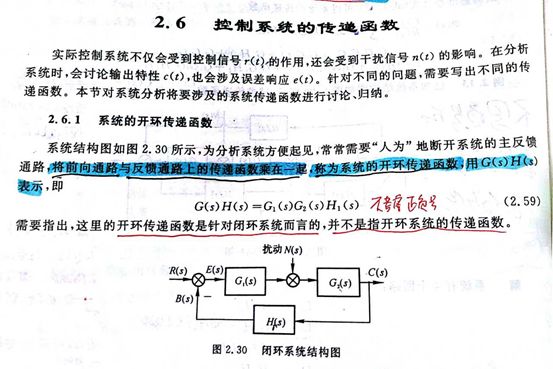
1 开环和闭环传递函数
众所周知,梅逊增益公式是用来求解传递函数的,既能求开环传函,也能求闭环传函。
求闭环传递函数,比如说常见的输出C(s)比上控制端输入R(s)、输出C(s)比上干扰输入N(s),以及误差传递函数,如控制输入端的误差传递函数 和 干扰输入端的误差传递函数。
求开环传函呢,事实上这里指的是一个闭环系统结构图中含有若干个小闭环时求它的开环传函。一般的求开环传递函数呢,我们只需要按照定义来求就行了,即:
注意啦!
如何求开环传递函数呢?
仔细看上图,上面已经说的很清楚了,断开主反馈通路,将前向通路与反馈通路上的传递函数乘在一起,G(s)H(s)乘在一起就是开环传递函数,不用考虑什么正负号。
开环传递函数会求了,接下来我们需要学会求解闭环传递函数!
如何求解闭环传递函数呢?
如果一个给定的结构框图不是上图这种简单形式的,那就要用梅逊公式来求了!毕竟梅逊公式的第一个使命就是求解闭环传递函数。
如果给定的结构框图是上图这种简单形式的,那么闭环传递函数就可以用一个简单的口诀来记了,什么口诀呢?
请看!
仔细对比下上图这四个闭环传递函数,无论是普通的控制输入作用下的闭环传递函数,或者是误差传递函数,都等于(1+开环传函) 分之 前向通道增益!
其实这个口诀也算作是梅逊公式的翻版吧,你想想看,梅逊公式的分母中那一个个回路,其实就是每个小闭环的开环传递函数啊,只不过在书写时,又把不接触的回路人为地乘在一起,分母中多了这些项而已。
为什么还要费大劲这样总结口诀呢?
因为只有在学习结构图等效变换和信号流图引入梅逊公式时,我们面对的是各种复杂的结构框图,各种大闭环里面附带小闭环,我们才用标准的梅逊公式去求解闭环传递函数。
什么叫复杂的结构框图,诺,就像下面这种图:
但是,
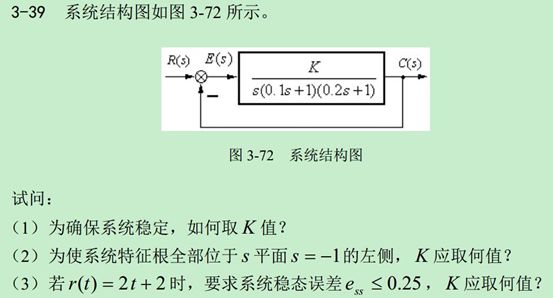
当我们学习到后边的章节时,遇到的结构框图,大部分是类似于图1的那种简易形式的,比如第三章时域分析的题(像下面这个题完全可以作为考研题,考查的知识点并不少)
题目源自于卢京潮版本第三章课后题
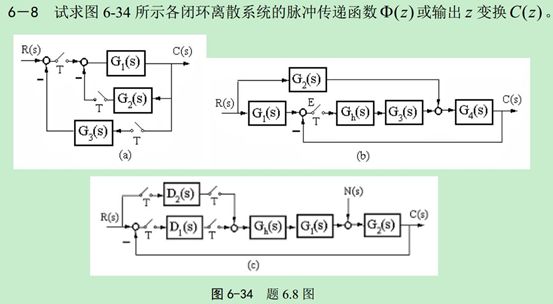
再如第六章离散系统的分析
第7章非线性系统的分析
很明显,上面这几张图,结构上就比较简单了,基本上可以看做是图一的小小延伸。
看到这里,其实你应该有这样的疑问:
宝刀君你讲的第三章时域分析的图应用这个口诀我还可以理解,至于第6章和第7章的图嘛,那都换了域了,甚至系统都变成非线性了,你这个口诀还能继续用吗?
或者说,你梅逊公式还能继续用吗?
能!
可以!
还能用!
因为这世上有一种人,他一生就只围绕着一个使命去做,比如司马迁写史记,孔子做教育,高斯玩数学,许渊冲做翻译,刘翔跨栏杆,梅逊公式也是一样,他一生也是如此,就是致力于解决经典自动控制原理各种问题的,为了判断系统的稳定性,梅逊公式会和闭环特征方程一起并肩作战,在前面打冲锋,做铺垫!
可以说,求传递函数,奠定了梅逊公式的江湖地位,让梅逊公式得以扬名立万!而和特征方程的结盟,则一起解决了经典自控典型问题!
这样说,有点煽情,你只是听着很爽很有画面感,但如果没掌握就体会不到,不如直接上题吧,大家伙一起开开眼!
2 离散系统中的应用
来一道西工大821自控2009年的真题吧,如图:
注意:干扰输入那,没有开关,因此求不出φn(s),只能将干扰输入和(1/s+1)绑定在一起做z变换,所以你看题目是让你求C(z)呢。
怎么写C(Z)呢,书上一般介绍的是逐步推导的方法,根据信号的流入流出,在比较点处写等式来推导,即:
书上都这样写,课后题的解答答案上更是如此,比如上面图6-34的第二个和第三个图对应的答案求解步骤如下:
这种方法好吗?
根据结构图等效推导出来的,没啥错的,但就是太麻烦了,书写太复杂,如果考试时也按这种方法来写,估计考生就崩溃了!
痛不欲生!
怎么办?谁来指条康庄大道?
没错,就是我宝刀君,我来告诉你吧!我给你支一招!
你仔细看下我这个解析过程,虽然理论上求不出传递函数(传递函数是个比值,是个分式,这道题不能求传函),但是在我的写法上,依然是借鉴了梅逊公式的思想,写出了一个分式!
这个分式的分子,是干扰输入信号和惯性环节(1/s+1)绑定在一起做的Z变换;
这个分式的分母,是回路中3个环节的Z变换!
可以说,形式上,依旧是采用的梅逊公式的思想!!!
反应过来了吗?
不知道我讲清楚了没?
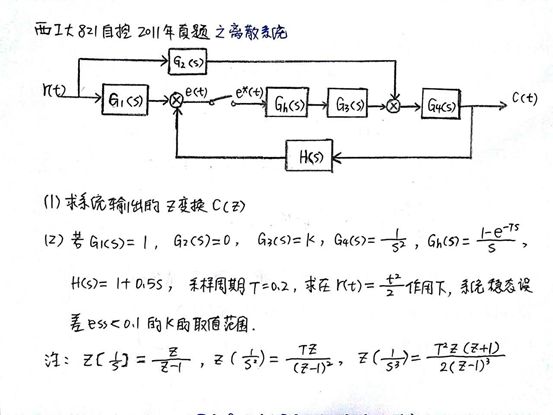
如果还没明白,可以继续看2011年的这道真题。
这道题也是一样,第一问让你求输出的Z变换。
这第一问要让我这种老手做,我3秒钟就可以给你说出答案!5秒钟给你写出答案!
分析下我第一问的答案吧,我仅仅是借鉴了梅逊公式的思想,分子写前向通道增益,分母写(1+开环传函)!
是不是清爽很多?
是不是感觉好神奇啊?
是不是觉得你只需要考虑在哪加那个(Z)就行了呀?(这是另一个话题了,后期再讲)
哈哈哈!
想象一下看文章的逆恍然大悟的样子,真开心!
幸甚至哉,歌以咏志!
3 非线性系统中的应用
除了离散域可以沿用,非线性系统的描述函数法分析中,依然可以用梅逊公式!
我们知道(即使你不知道也要假装知道),运用描述函数法分析系统的稳定性时,必须满足3个条件,其中一个首要的的条件是:非线性系统的结构图可以简化成只有一个非线性环节N(A) 和 一个线性部分G(s)相串联的的典型形式。
基于这个条件,很自然,当我们拿到一道非线性系统稳定性分析的题目时,就要考虑怎样找出它的等效线性环节和等效非线性环节!
怎样求?
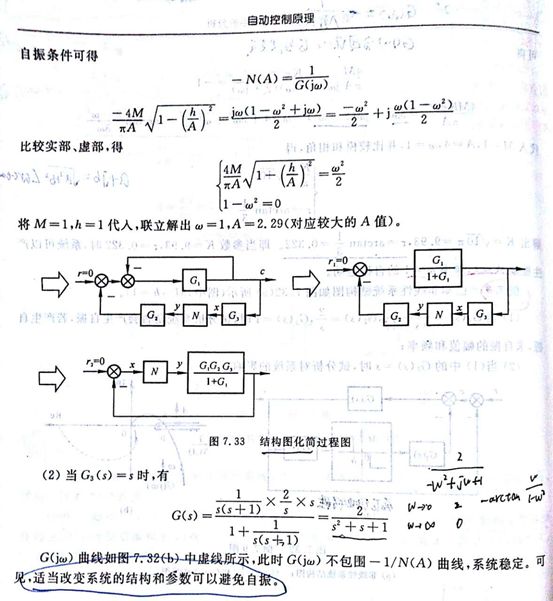
以题为例,比如课本上给的这个例题,它采用的是结构图等效变换的手法:
解法中提到的结构图化简过程,图7.33在这里:
坦白讲,这个化简过程,好多学生看了后都觉得头晕!
每次教学授课过程中,不少学生愁眉苦脸的跑来问我这图是咋化简的。
我说,我不想分析它这个方法,但是我有更好的方法介绍给你,你愿不愿意听啊?
当然想听了,什么方法啊?
当然是借助于梅逊公式和闭环特征方程啊!你看看我求解等效线性环节、等效非线性环节的推导过程,纯粹的数学手法!
哎呦,我滴天哪!
这世间竟有如此巧妙的方法!!!
没有复杂的图形推导,没有难以理解的概念,只有一个梅逊公式,前向通道只有一个,就是那个G1,回路有两个,按照梅逊公式的定义,或者直接用我讲的那个口诀:(1+开环传函) 分之 前向通道增益 往那写就行了!
妙哉妙哉!
是不是感觉还不过瘾,那就再举一例!
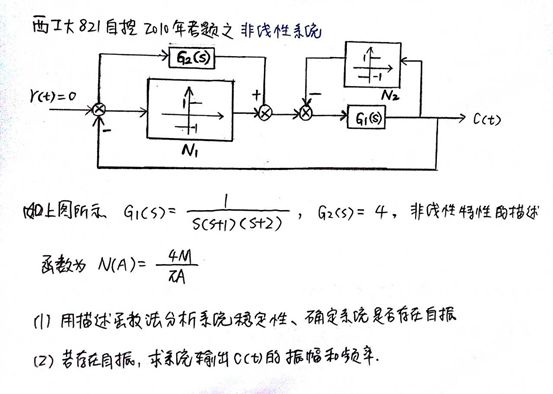
2010年的这道题
还是同样的处理方法,借助梅逊公式和闭环特征方程来求,前向通道有两个,分别是G2G1,N1G1,有3个回路,N1G1,N2G1,G2G1,这三个回路两两接触。
写出梅逊公式后,接下来借助于闭环特征方程,配凑出它的等效闭环特征方程,即配凑1+N(A)*G(S)=0,想办法把这个“1”给凑出来!
解法如下:
4 总结
讲完了!
感觉怎么样?
有木有一种受益匪浅的感觉?
哈哈,也许你现在还感受不到,放心吧,我相信等你做第六章和第七章相关题的时候,还会跑回来继续研究我这篇文章的!说近点,你在学习根轨迹求等效开环传递函数时,会过来认真看我这最后一题的解析图片的。
到那时,你就正儿八经的体会到梅逊公式和闭环特征方程这套组合拳的精妙了!
备注:本篇文章的知识点内容图片来自于书籍:
卢京潮. 自动控制原理-第2版[M]. 西北工业大学出版社, 2009.
在此,向卢京潮老师及其教材编写团队表示感谢!
*****************************************************
哈喽,大家好!我是宝刀君,微信公众号:考研摆渡人宝刀君,ID:BDJ0501,专注考研数学、自动控制原理的辅导,文章风格:有料、有趣、有深度!
如果您觉得我的文章对您理解知识点有帮助,麻烦伸出可爱的指头顺手帮我点个赞,鼓励我继续创作,如果您这样做了,非常感谢~~~