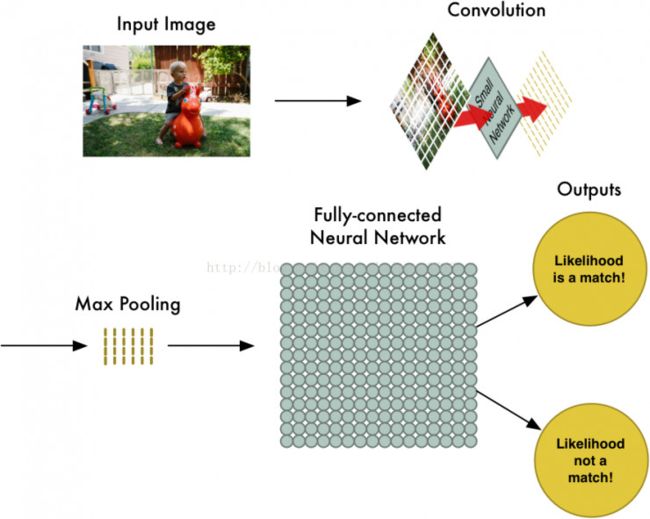
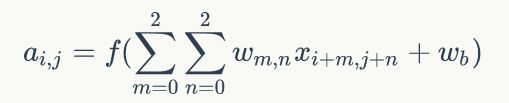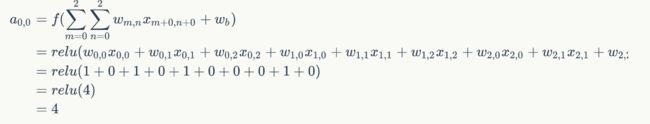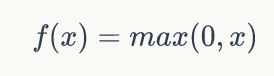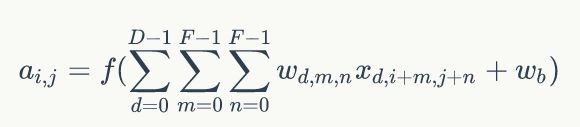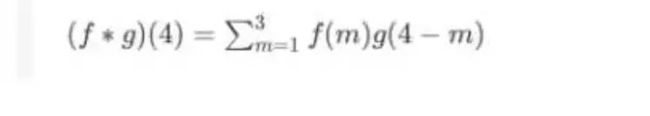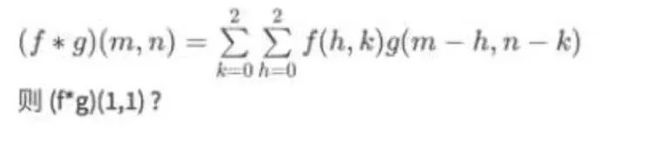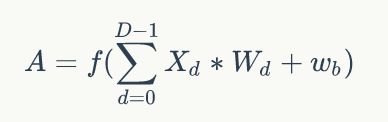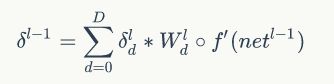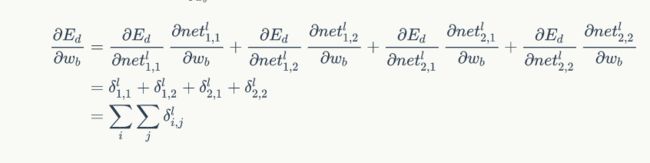对于图片的识别来说,全连接网络无疑节点数太多了,对于一个28*28的图片,输入节点数就达到784个,更别说一个更大的图片。所以为了实现计算的简化以及性能的优化处理这就提出了卷积神经网络。
卷积神经网络
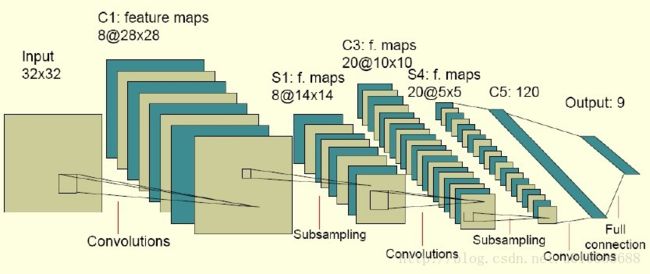
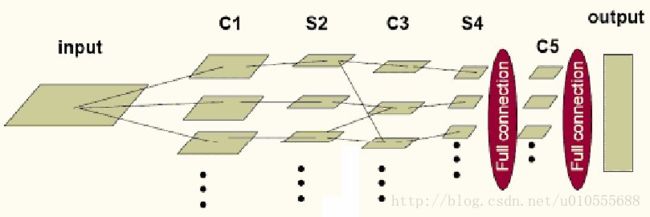
卷积神经网络CNN的结构一般包含这几个层:
1.输入层(input):用于数据的输入
2.卷积层(convolution):使用卷积核进行特征提取和特征映射
3.激励层:由于卷积也是一种线性运算,因此需要增加非线性映射
4.池化层(Max Pooling):进行下采样,对特征图稀疏处理,减少数据运算量。
5.全连接层(Fully-connexted):通常在CNN的尾部进行重新拟合,减少特征信息的损失
6.输出层(output):用于输出结果
当然中间还可以使用一些其他的功能层:
1.归一化层(Batch Normalization):在CNN中对特征的归一化
2.切分层:对某些(图片)数据的进行分区域的单独学习
3.融合层:对独立进行特征学习的分支进行融合
CNN层次结构
输入层
在CNN的输入层中,(图片)数据输入的格式 与 全连接神经网络的输入格式(一维向量)不太一样。CNN的输入层的输入格式保留了图片本身的结构。
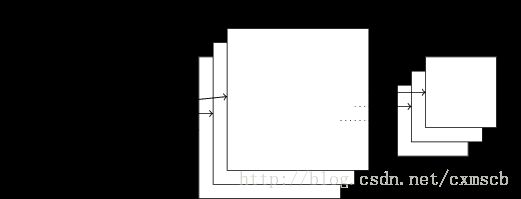
对于黑白的 28×28 的图片,CNN的输入是一个 28×28 的的二维神经元,如下图所示
对于RGB格式的28×28图片,CNN的输入则是一个 3×28×28 的三维神经元(RGB中的每一个颜色通道都有一个 28×28 的矩阵),如下图所示:
卷积层
假设输入的是一个 28×28 的的二维神经元,我们定义5×5 的 一个 local receptive fields(感受视野),即 隐藏层的神经元与输入层的5×5个神经元相连,这个5*5的区域就称之为Local Receptive Fields,如下图所示:
可类似看作:隐藏层中的神经元 具有一个固定大小的感受视野去感受上一层的部分特征。在全连接神经网络中,隐藏层中的神经元的感受视野足够大乃至可以看到上一层的所有特征。
而在卷积神经网络中,隐藏层中的神经元的感受视野比较小,只能看到上一次的部分特征,上一层的其他特征可以通过平移感受视野来得到同一层的其他神经元,由同一层其他神经元来看:
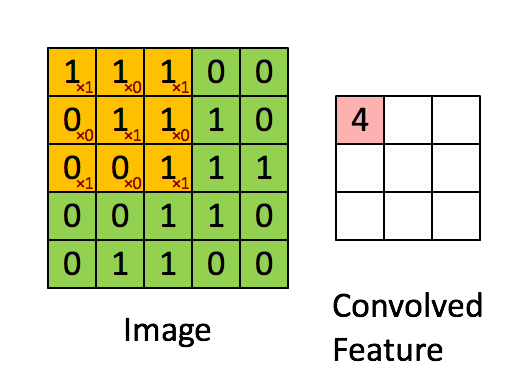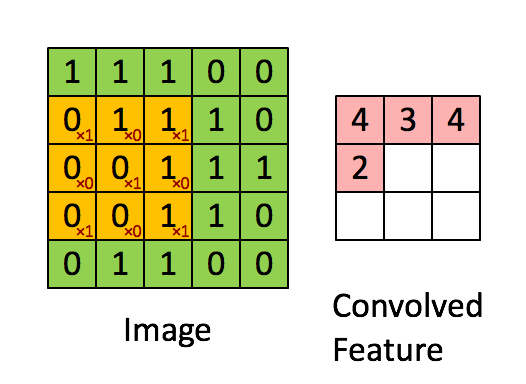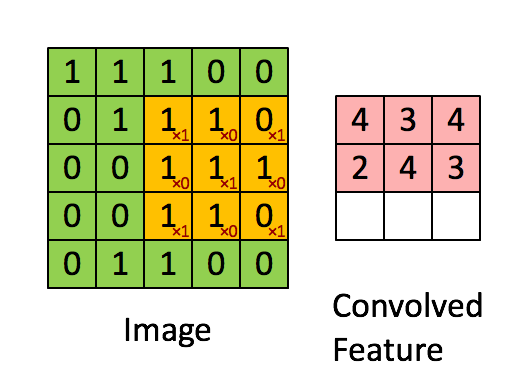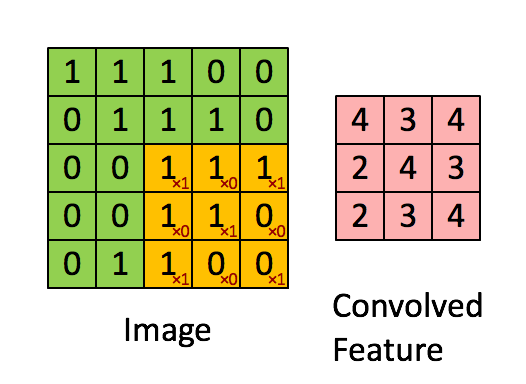
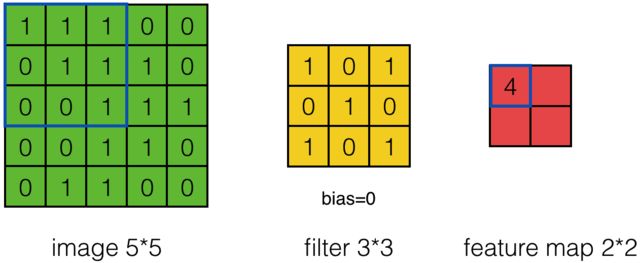
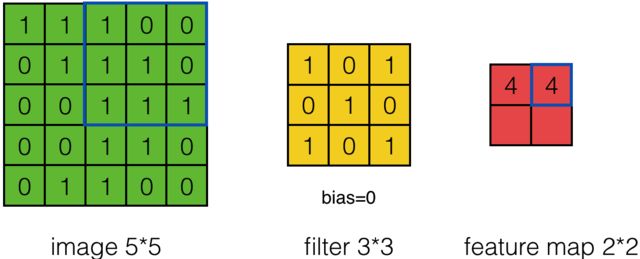
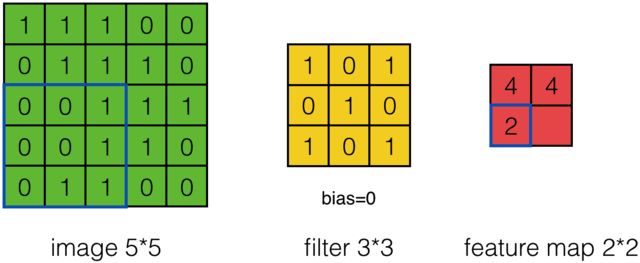
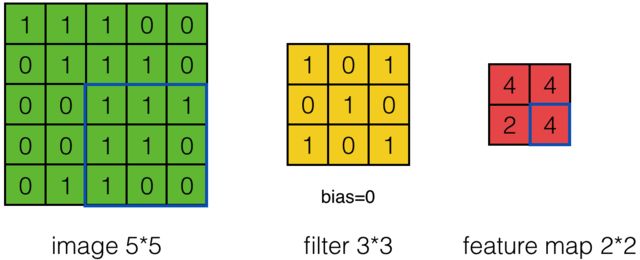
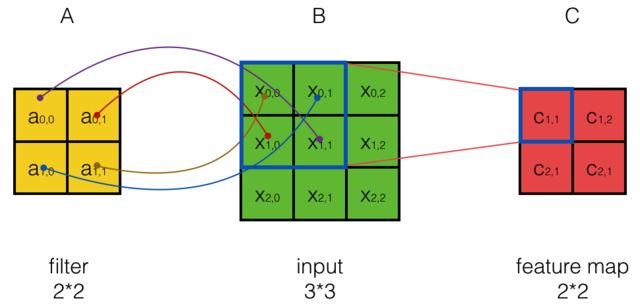
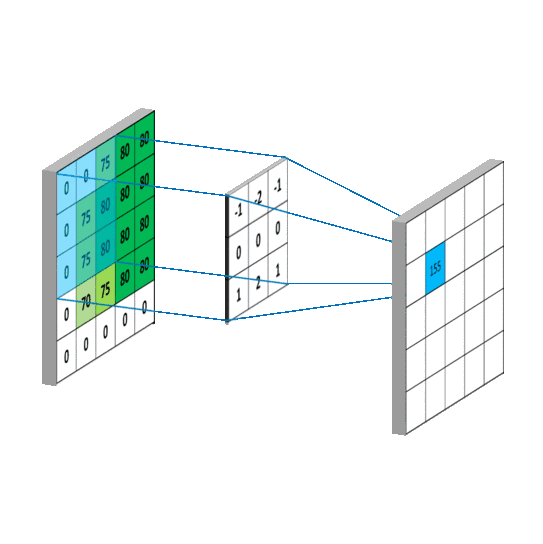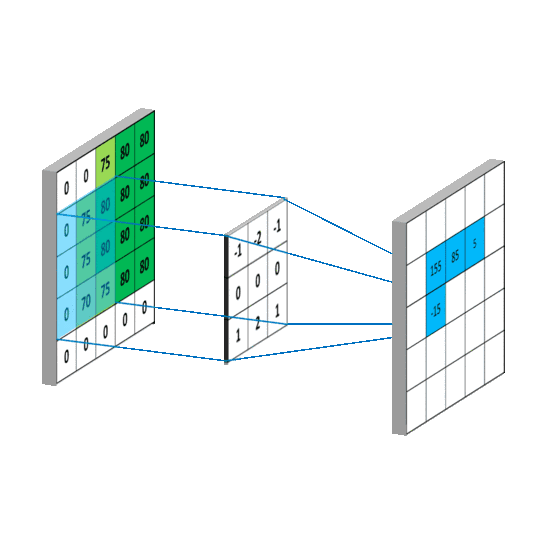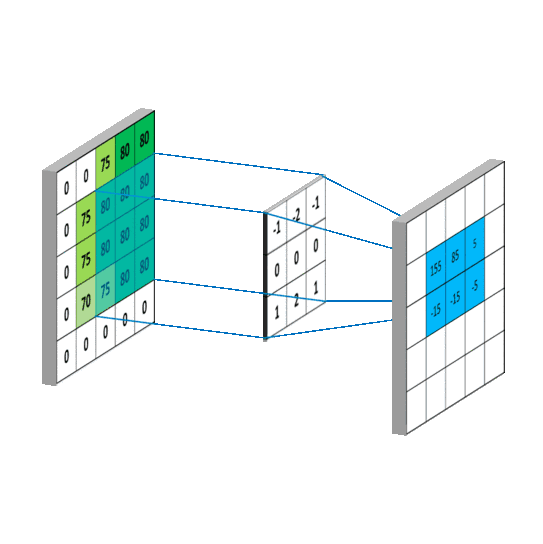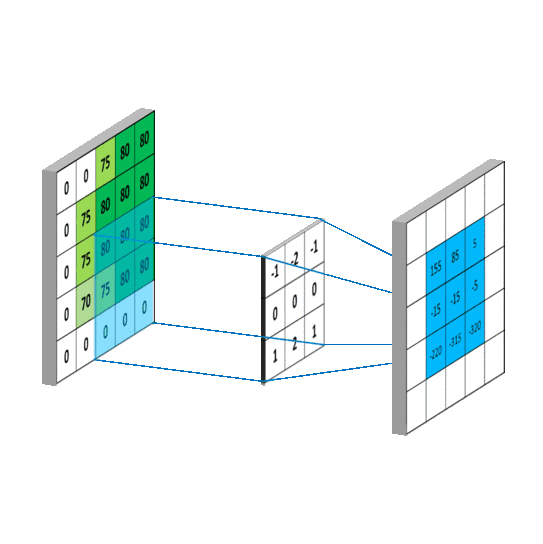
其计算过程用以下动画表示:
对于生成的隐藏层来说,其上的值用a表示,x表示输入,w表示权值:
例如,对Convolved Feature图左上角元素来说,其卷积计算方法为:
其中relu为激活函数。
激活函数
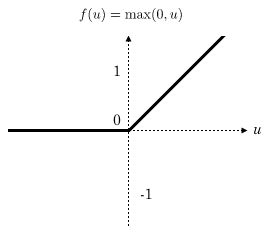
Relu函数的定义是:
函数的图形表示:
函数的优势有很多,不在多说。
这是单步的情况下的推导,当我们把步数调到2时:
结果就是丢掉了步数为1时候的中间项。
由此我们可以总结出,通过input image和权重filter来推出隐藏层即Convolved Feature map的值的公式:
其中d表示卷积的通道数目。
用动画表示:
当然对于这样的式子并不满足,这时就想到用数学来优化它。
数学推导
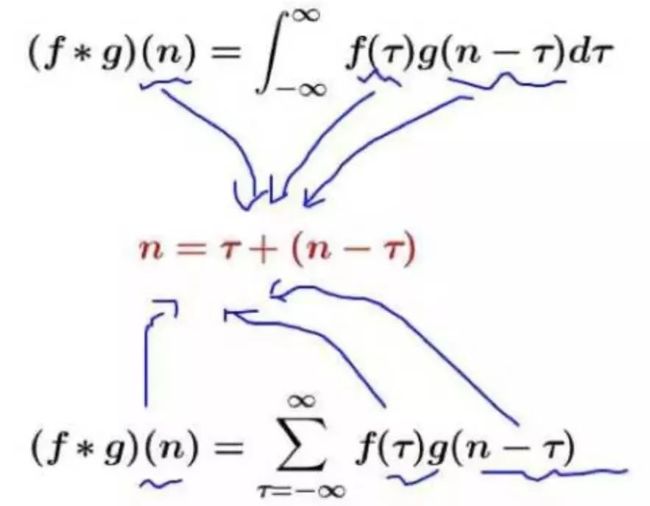
数学中的卷积:
特点:
离散卷积
举个例子,丢骰子时加起来要等于4的概率是多少?
用卷积公式表示就是:
这只是一维的表示。下面来看二维的离散:
二维离散的卷积:
在二维的离散计算结果表示:
我们可以看出数学上的卷积公式和我们使用的Convolved Feature map的值的计算的方式的差别:
数学上:
而我们使用的方式是:
a0,0x0,0+a0,1x0,1+a1,0x1,0+a1,1x1,1
所以还需要将数学上的额卷积公式进行变换,已达到我们需要的效果。
即:
首先,我们把矩阵A翻转180度,然后再交换A和B的位置(即把B放在左边而把A放在右边。卷积满足交换率,这个操作不会导致结果变化)。
表现为:
这样就直接使用向量计算来满足我们的需要了。 _
用个动画展示:
池化层
接下来就到了池化层。
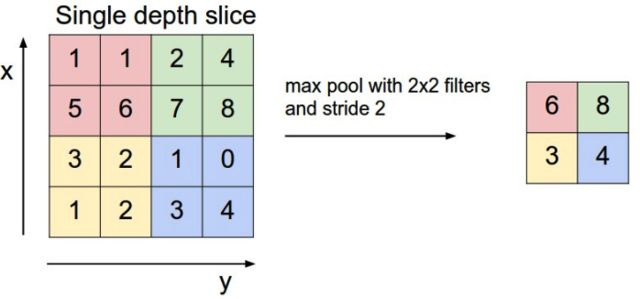
池化层(Pooling)层主要的作用是下采样,通过去掉卷积层(Convolved Feature map)中不重要的样本,进一步减少参数数量。Pooling的方法很多,最常用的是Max Pooling。
简单地讲就是去一定范围的最大值。
举个例子:
后可将 3 个 24×24 的 feature map 下采样得到 3 个 12×12 的特征矩阵:
除了Max Pooing之外,常用的还有Mean Pooling——取各样本的平均值。
经过几轮的这种卷积、池化操作,将最后取得的特征传递给一个全连接网络,这就实现了一个CNN网络的向前传播。
当然,为了训练权值,我们还需要用到向后传播。
向后传播
对于向后传播,我们使用的依旧是梯度下降的方式。
先从池化层说起。
池化层
在网络中池化层并没有涉及到学习的功能,所以只是将误差进行传递即可。
对于Max Pooing
因为Max Pooing的向前传播,就是取得局部的最大值,所以误差传递,也只是将这个误差传递给局部的最大值的位置,其他位置为0。
对于Mean Pooling
因为Mean Pooling的向前传播,就是取得局部的平均值,所以误差传递,就是将下一层的误差项的值会平均分配到上一层对应区块中的所有神经元。
卷积层
误差传递
用net表示第L行神经元的加权输入。
具体推导过程请看【零基础入门深度学习(4) - 卷积神经网络】一文,不得不说大神写的很详细。感谢大神的分享。
梯度
根据反向梯度的法则,我们需要求得w变化最小值。
推导过程同上。
也就是偏置项的梯度就是卷积层所有误差项之和。
代码实现
代码使用tensorflow工具。
简单介绍一下tensorflow:
TensorFlow是谷歌基于DistBelief进行研发的第二代人工智能学习系统,其命名来源于本身的运行原理。Tensor(张量)意味着N维数组,Flow(流)意味着基于数据流图的计算,TensorFlow为张量从流图的一端流动到另一端计算过程。TensorFlow是将复杂的数据结构传输至人工智能神经网中进行分析和处理过程的系统。
TensorFlow可被用于语音识别或图像识别等多项机器学习和深度学习领域,对2011年开发的深度学习基础架构DistBelief进行了各方面的改进,它可在小到一部智能手机、大到数千台数据中心服务器的各种设备上运行。TensorFlow将完全开源,任何人都可以用。
不得不说这个工具的强大。
首先需要安装anaconda。Anaconda指的是一个开源的Python发行版本,其包含了conda、Python等180多个科学包及其依赖项。下载过程自行百度,不在多说。
具体解释代码注释已经详细解释,也不多说了。
model.py(CNN模型类)
# -*- ecoding:utf-8 -*-
import tensorflow as tf
class model():
def __init__(self):
#创建图片节点(占位符模式)形状为784 列
self.x_image = tf.placeholder(tf.float32, [None, 784])
#创建期望输出值节点(占位符模式)形状为 10 列
self.ylabel = tf.placeholder(tf.float32, [None, 10])
#重新分配排列(-1为自动计算排列值) 图像输入为 (宽 28 高 28 通道 1 -1位图片数量)
self.x = tf.reshape(self.x_image, [-1,28,28,1])
#first layer
#命名域
with tf.name_scope('conv1'):
#truncated_normal生成截断正态分布随机数 标准差为0.1
#创建变量卷积层权值 filter为( 高 5 宽 5 通道数 1 卷积核个数 32)
self.W_conv1 = tf.Variable(tf.truncated_normal([5,5,1,32], stddev=0.1))
#创建常数偏移量
self.b_conv1 = tf.Variable(tf.constant(0.1, shape=[32]))
#Converlution
#进行卷积 tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)
#strides 步长(卷积时在图像每一维的步长,这是一个一维的向量,长度4)
#padding:string类型的量,只能是"SAME","VALID"其中之一,这个值决定了不同的卷积方式
#use_cudnn_on_gpu:bool类型,是否使用cudnn加速,默认为true
self.h_conv1 = tf.nn.conv2d(self.x, self.W_conv1, strides=[1,1,1,1], padding='SAME') + self.b_conv1
#输出值计算
# W = ( W - F + 2P)/S + 1
# H = ( H - F + 2P)/S + 1
#输出值为(高 24 宽 24 通道数 32)
#激活函数
self.h_convRelu1 = tf.nn.relu(self.h_conv1)
#pooling
with tf.name_scope('pool1'):
#设定池化
#tf.nn.max_pool(value, ksize, strides, padding, name=None)
#ksize:池化窗口的大小,取一个四维向量,一般是[1, height, width, 1],不在batch和channels上做池化
#strides:和卷积类似,窗口在每一个维度上滑动的步长,一般也是[1, stride,stride, 1]
#padding:和卷积类似,可以取'VALID' 或者'SAME'
self.h_pool1 = tf.nn.max_pool(self.h_convRelu1, ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME')
#输出值计算
#SAME模式:
#W=W/S
#H=H/S
#VALID模式:
# W =(W - F + 1)/S
# H =(H - F + 1)/S
#输出值为 (高 12 宽 12 通道数 32)
#second layer
with tf.name_scope('conv2'):
#创建变量卷积层权值 filter为( 高 5 宽 5 通道数 32 卷积核个数 64) 标准差为0.1
self.W_conv2 = tf.Variable(tf.truncated_normal([5,5,32,64], stddev=0.1))
#创建常数偏移量
self.b_conv2 = tf.Variable(tf.constant(0.1, shape=[64]))
#Converlution
#进行卷积
self.h_conv2 = tf.nn.conv2d(self.h_pool1, self.W_conv2, strides=[1,1,1,1], padding='SAME') + self.b_conv2
#输出为 (高 7 宽 7 通道数 64)
#激活函数
self.h_convRelu2 = tf.nn.relu(self.h_conv2)
#pooling
with tf.name_scope('pool2'):
#设定池化
self.h_pool2 = tf.nn.max_pool(self.h_convRelu2, ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME')
#卷积部分最后输出为(高 7 宽 7 通道数 64)
#全连接网络
with tf.name_scope('fc1'):
##构建全连接的输入层权重 输入为 7*7*64个节点 隐藏层为 1024个节点
self.W_fc1 = tf.Variable(tf.truncated_normal([7*7*64, 1024], stddev=0.1))
##构建全连接的输入层偏移量
self.b_fc1 = tf.Variable(tf.constant(0.1,shape=[1024]))
#重新设置输入数据的样式
self.h_pool2_flat = tf.reshape(self.h_pool2, [-1,7*7*64])
#进行矩阵乘法
self.h_fc1 = tf.matmul(self.h_pool2_flat, self.W_fc1) + self.b_fc1
#激活函数
self.h_fcRelu1 = tf.nn.relu(self.h_fc1)
#防止过拟合
with tf.name_scope('dropout'):
self.keep_prob = tf.placeholder(tf.float32)
#tf.nn.dropout(x, keep_prob, noise_shape=None, seed=None,name=None)
#keep_prob: 设置神经元被选中的概率,在初始化时keep_prob是一个占位符,
self.h_fcdrop1 = tf.nn.dropout(self.h_fcRelu1, self.keep_prob)
#输出层
with tf.name_scope('fc2'):
#设定权重 输出层为10个节点
self.W_fc2 = tf.Variable(tf.truncated_normal([1024, 10], stddev=0.1))
#偏移量
self.b_fc2 = tf.Variable(tf.constant(0.1, shape=[10]))
#矩阵相乘 得到输出
self.y_conv = tf.matmul(self.h_fcdrop1, self.W_fc2) + self.b_fc2
#计算代价
with tf.name_scope('loss'):
#tf.nn.softmax_cross_entropy_with_logits(logits, labels, name=None)
#logits : 就是神经网络最后一层的输出
#labels : 实际的标签
self.cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=self.ylabel, logits=self.y_conv)
#tf.reduce_mean(input_tensor, reduction_indices=None, keep_dims=False, name=None)
#求取平均值
self.cross_entropy = tf.reduce_mean(self.cross_entropy)
#梯度求解
with tf.name_scope('adam_optimizer'):
#Adam优化算法:是一个寻找全局最优点的优化算法。
#寻找误差最小的点
self.train_step = tf.train.AdamOptimizer(1e-4).minimize(self.cross_entropy)
with tf.name_scope('accuracy'):
#tf.argmax 返回向量中最大的那个索引号
#tf.equal 比较两个矩阵或者向量是否相等
#tf.cast 类型转换
#tf.reduce_mean 求取平均值
#计算误差率
self.correct_prediction = tf.equal(tf.argmax(self.y_conv, 1), tf.argmax(self.ylabel,1))
self.correct_prediction = tf.cast(self.correct_prediction, tf.float32)
self.accuracy = tf.reduce_mean(self.correct_prediction)
input_data.py(获取MNIST数据集)
"""Functions for downloading and reading MNIST data."""
from __future__ import print_function
import gzip
import os
import urllib
import numpy
SOURCE_URL = 'http://yann.lecun.com/exdb/mnist/'
def maybe_download(filename, work_directory):
"""Download the data from Yann's website, unless it's already here."""
if not os.path.exists(work_directory):
os.mkdir(work_directory)
filepath = os.path.join(work_directory, filename)
if not os.path.exists(filepath):
filepath, _ = urllib.urlretrieve(SOURCE_URL + filename, filepath)
statinfo = os.stat(filepath)
print('Succesfully downloaded', filename, statinfo.st_size, 'bytes.')
return filepath
def _read32(bytestream):
dt = numpy.dtype(numpy.uint32).newbyteorder('>')
return numpy.frombuffer(bytestream.read(4), dtype=dt)[0]
def extract_images(filename):
"""Extract the images into a 4D uint8 numpy array [index, y, x, depth]."""
print('Extracting', filename)
with gzip.open(filename) as bytestream:
magic = _read32(bytestream)
if magic != 2051:
raise ValueError(
'Invalid magic number %d in MNIST image file: %s' %
(magic, filename))
num_images = _read32(bytestream)
rows = _read32(bytestream)
cols = _read32(bytestream)
#print num_images
#print rows
#print cols
buf = bytestream.read(rows * cols * num_images)
data = numpy.frombuffer(buf, dtype=numpy.uint8)
data = data.reshape(num_images, rows, cols, 1)
return data
def dense_to_one_hot(labels_dense, num_classes=10):
"""Convert class labels from scalars to one-hot vectors."""
num_labels = labels_dense.shape[0]
index_offset = numpy.arange(num_labels) * num_classes
labels_one_hot = numpy.zeros((num_labels, num_classes))
labels_one_hot.flat[index_offset + labels_dense.ravel()] = 1
return labels_one_hot
def extract_labels(filename, one_hot=False):
"""Extract the labels into a 1D uint8 numpy array [index]."""
print('Extracting', filename)
with gzip.open(filename) as bytestream:
magic = _read32(bytestream)
if magic != 2049:
raise ValueError(
'Invalid magic number %d in MNIST label file: %s' %
(magic, filename))
num_items = _read32(bytestream)
buf = bytestream.read(num_items)
labels = numpy.frombuffer(buf, dtype=numpy.uint8)
if one_hot:
return dense_to_one_hot(labels)
return labels
class DataSet(object):
def __init__(self, images, labels, fake_data=False):
if fake_data:
self._num_examples = 10000
else:
assert images.shape[0] == labels.shape[0], (
"images.shape: %s labels.shape: %s" % (images.shape,
labels.shape))
self._num_examples = images.shape[0]
# Convert shape from [num examples, rows, columns, depth]
# to [num examples, rows*columns] (assuming depth == 1)
assert images.shape[3] == 1
images = images.reshape(images.shape[0],
images.shape[1] * images.shape[2])
# Convert from [0, 255] -> [0.0, 1.0].
images = images.astype(numpy.float32)
images = numpy.multiply(images, 1.0 / 255.0)
self._images = images
self._labels = labels
self._epochs_completed = 0
self._index_in_epoch = 0
@property
def images(self):
return self._images
@property
def labels(self):
return self._labels
@property
def num_examples(self):
return self._num_examples
@property
def epochs_completed(self):
return self._epochs_completed
def next_batch(self, batch_size, fake_data=False):
"""Return the next `batch_size` examples from this data set."""
if fake_data:
fake_image = [1.0 for _ in xrange(784)]
fake_label = 0
return [fake_image for _ in xrange(batch_size)], [
fake_label for _ in xrange(batch_size)]
start = self._index_in_epoch
self._index_in_epoch += batch_size
if self._index_in_epoch > self._num_examples:
# Finished epoch
self._epochs_completed += 1
# Shuffle the data
perm = numpy.arange(self._num_examples)
numpy.random.shuffle(perm)
self._images = self._images[perm]
self._labels = self._labels[perm]
# Start next epoch
start = 0
self._index_in_epoch = batch_size
assert batch_size <= self._num_examples
end = self._index_in_epoch
return self._images[start:end], self._labels[start:end]
def read_data_sets(train_dir, fake_data=False, one_hot=False):
class DataSets(object):
pass
data_sets = DataSets()
if fake_data:
data_sets.train = DataSet([], [], fake_data=True)
data_sets.validation = DataSet([], [], fake_data=True)
data_sets.test = DataSet([], [], fake_data=True)
return data_sets
TRAIN_IMAGES = 'train-images-idx3-ubyte.gz'
TRAIN_LABELS = 'train-labels-idx1-ubyte.gz'
TEST_IMAGES = 't10k-images-idx3-ubyte.gz'
TEST_LABELS = 't10k-labels-idx1-ubyte.gz'
VALIDATION_SIZE = 5000
local_file = maybe_download(TRAIN_IMAGES, train_dir)
train_images = extract_images(local_file)
local_file = maybe_download(TRAIN_LABELS, train_dir)
train_labels = extract_labels(local_file, one_hot=one_hot)
local_file = maybe_download(TEST_IMAGES, train_dir)
test_images = extract_images(local_file)
local_file = maybe_download(TEST_LABELS, train_dir)
test_labels = extract_labels(local_file, one_hot=one_hot)
validation_images = train_images[:VALIDATION_SIZE]
validation_labels = train_labels[:VALIDATION_SIZE]
train_images = train_images[VALIDATION_SIZE:]
train_labels = train_labels[VALIDATION_SIZE:]
data_sets.train = DataSet(train_images, train_labels)
data_sets.validation = DataSet(validation_images, validation_labels)
data_sets.test = DataSet(test_images, test_labels)
return data_sets
traincnn.py(开始训练模型)
import tensorflow as tf
import input_data
from model import model
class TrainCnn():
def __init__(self):
#创建模型
self.network = model()
#创建图
self.sess = tf.Session()
#获取MNIST数据集
self.data = input_data.read_data_sets('./data/', one_hot=True)
def train(self):
#每次读取图片大小
batch_size = 100
#开始计算
self.sess.run(tf.global_variables_initializer())
#计算20000次
for i in range(20000):
batch = self.data.train.next_batch(100)
#输出错误率
if i%1==0:
realrate,cross = self.sess.run([self.network.accuracy, self.network.cross_entropy], feed_dict={self.network.x_image:batch[0], self.network.ylabel:batch[1], self.network.keep_prob:1.0})
print ('step %d, training accuracy:%g ,cross_entropy:%g' %(i, realrate, cross))
#训练网络
self.sess.run(self.network.train_step, feed_dict={self.network.x_image:batch[0], self.network.ylabel:batch[1], self.network.keep_prob:0.5})
if __name__ == '__main__':
app = TrainCnn()
app.train()
运行结果
只截取了一部分的数值,训练时间较长,获取大量练习后能达到准确率为0.95以上。
OK,打完收工。_
参考
Deep Learning模型之:CNN卷积神经网络(一)深度解析CNN
https://blog.csdn.net/qq_28743951/article/details/70924339
零基础入门深度学习(4) - 卷积神经网络
https://www.zybuluo.com/hanbingtao/note/485480
【CNN】一文读懂卷积神经网络CNN
https://blog.csdn.net/np4rHI455vg29y2/article/details/78958121
手把手教你用 TensorFlow 实现卷积神经网络(附代码)
https://www.leiphone.com/news/201705/6Zi5evpIaKJRHsJj.html
CNN卷积神经网络原理简介+代码详解
https://blog.csdn.net/haluoluo211/article/details/77466961
TF-卷积函数 tf.nn.conv2d 介绍
https://www.cnblogs.com/qggg/p/6832342.html
TensorFlow中CNN的两种padding方式“SAME”和“VALID”
https://blog.csdn.net/wuzqchom/article/details/74785643