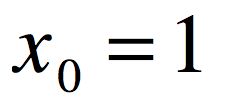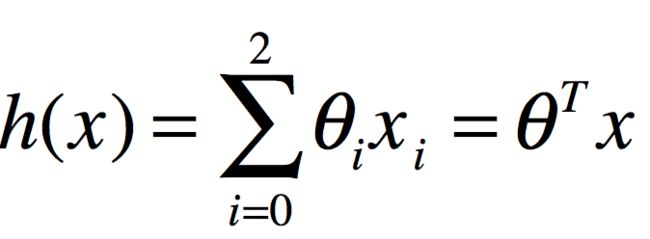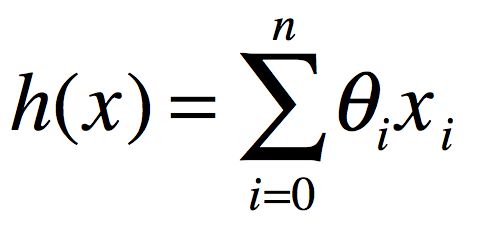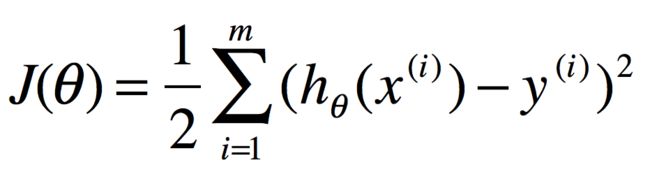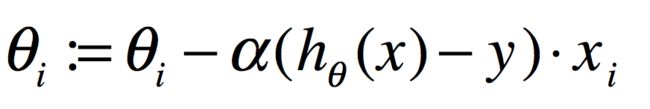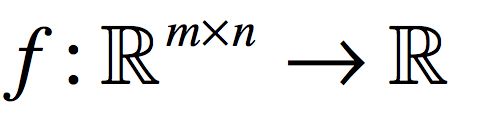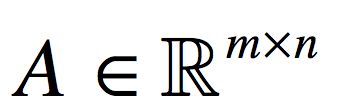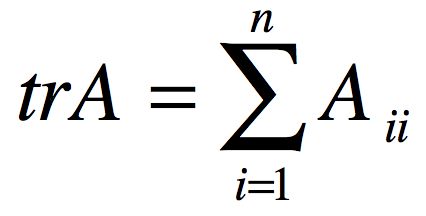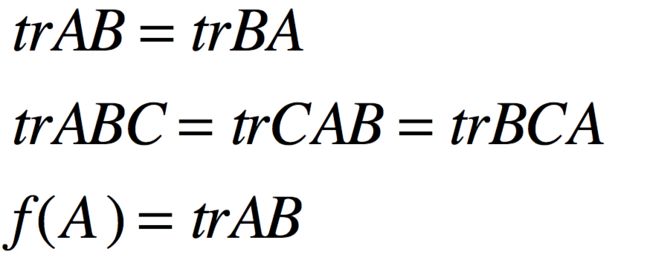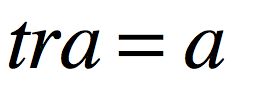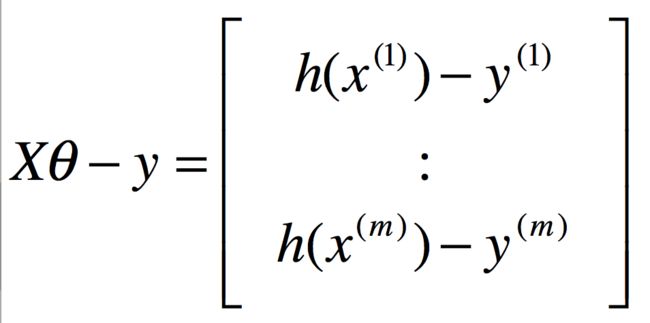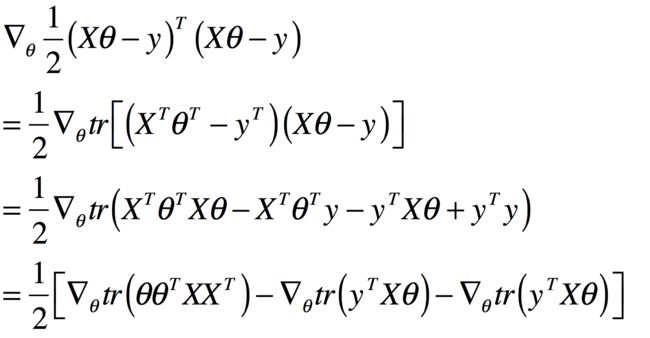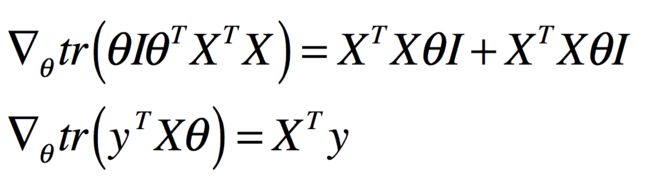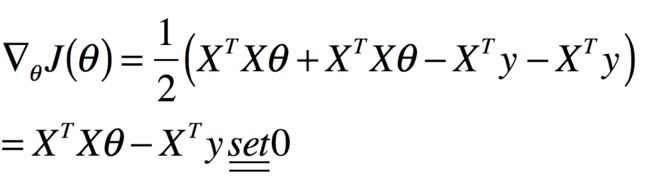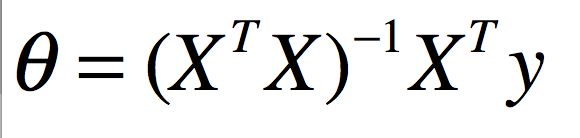jd.com本节课主要讲了三方面内容
线性回归
梯度下降
正规方程组(高能预警)
一、线性回归
以自动驾驶为例,之所以这个问题是监督学习,是因为机器可以从人类司机那里学习知识。其中,输入的是道路情景的照片,输出的是汽车行驶的方向。人类为汽车提供了一系列正确的行驶方向,之后会产生更多的“正确的”行驶方向,以确保汽车始终行驶在路上。由于汽车尝试预测表示行驶方向的连续变量的值,所以称之为回归问题。
以下是回归问题的思维导图
先列出一些参数的意义
m:训练样本
n:特征数目
x:输入变量(特征)
y:输出变量
(x,y):训练样本
i :第 i 行
让我们以上一节提到的房屋价格预测问题为例,这里的输入x表示房屋的尺寸、卧室数量等,输出y表示房屋的价格。我们已经有了一些数据样本,即xi, yi,目标是找到一个从x到y的函数,使得当输入x的时候,该函数能够输出正确的y的预测值。
首先,我们需要确定怎样表示这个函数,让我们考虑最简单的线性模型。当只考虑房屋大小时,构造一个一元函数,可以用如下函数
当引入两个变量(房屋尺寸与卧室数量)的时候,函数变为:
为了便于将整个公式写的更简洁,定义
于是,公式可写成
这里,n表示学习问题中特征的数目
接下来,我们怎样选取参数,能让假设h对所有的房屋做出准确的预测呢?
基于这个训练集合,给定一些特征x,以及正确的价格y,我们选择合适参数希望算法预测和实际价格的平方差尽可能的小。对于m个样本, 我们定义
于是,问题就转变成如何让J(\theta)最小化,下面讲几个使J最小的算法
二、搜索算法
我们先给参数向量一个初始值
持续改变参数向量,使J不断减小,直到找到一个最小值。
梯度下降算法
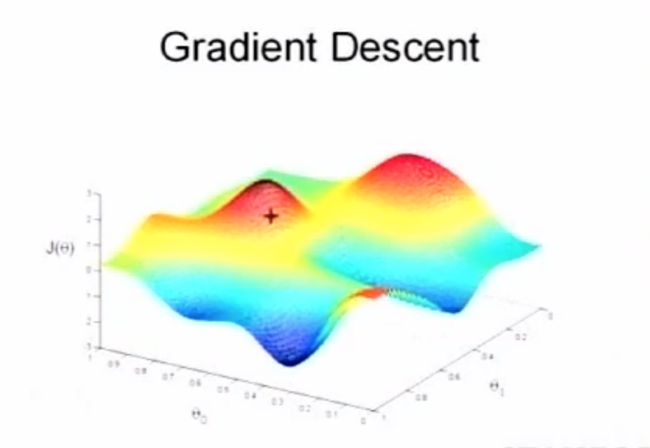
梯度下降算法的思想是,我们要选取一个初使点,可能是0向量,也可能是一个随机生成的点。想象看到的图形是一个三维地表
想象这个图描述的是你所处的环境,你的周围有很多小山。你站在其中一点,转一圈,然后选择下山最快的路,走一步,继续转一圈,再选择下山最快的路,再走一步。事实上这个下山最快的方向正是梯度的方向,直到你达到了这个山的最低点,也就是这个函数的一个局部最小值。
梯度下降的一个性质是它一定会结束, 在这个例子中,我们最终停在了左下角的这个点上,我们注意到,梯度下降找到的局部最小值会依赖于参数初始值。
那么整个梯度下降算法的过程可以写成如下的迭代公式:
我们只需要按照这个公式反复不停地迭代,就能够逐渐逼近最优的\theta_i的数值。在这个公式中,最棘手的就是J对于\theta的偏导数,让我们来看看在线性模型中,它应该怎样计算呢?
所以
这是数据只有一个样本时候的共识,假设我们有m个训练样本,那么就按照下面的公式计算:
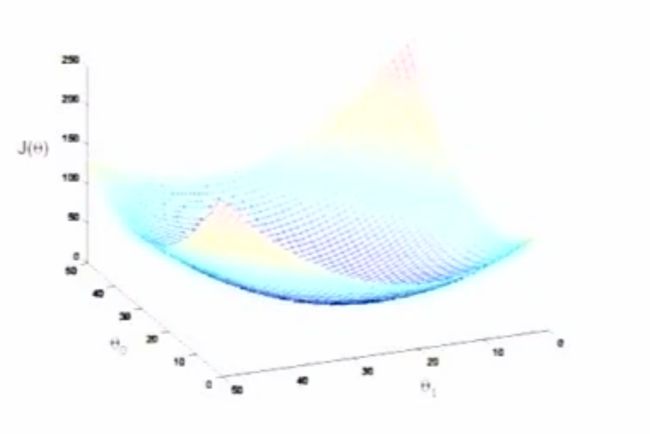
在这个线性模型中,目标函数J实际上并不向给你们展示的那个图形那么复杂,会有多个局地最优解。实际上,这种通常的平方函数,仅仅是一个二次函数,所以会得到一个漂亮的碗的形状,它只有一个全局最小值。
当快接近最优值时,步伐会越来越小,当达到局部最小值时,梯度也会减为0。
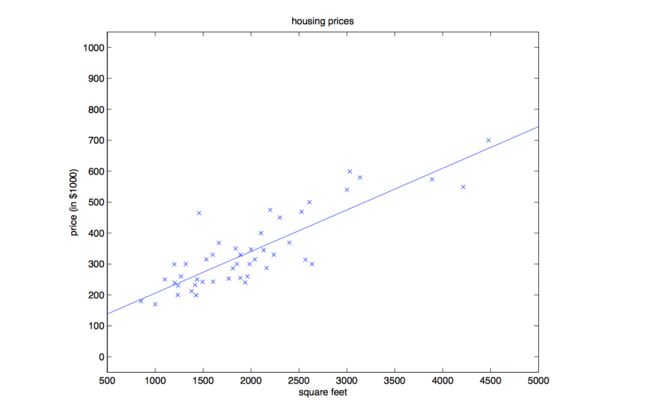
还是以房价图为例,我们经过几次迭代后,得到了这组数据的最小二乘拟合。
所以,我们可以用迭代公式求解放假预测的问题。
迭代公式可以一直工作下去,那么到什么时候停止呢?
有两种不同的方法来检测收敛
- 一种是检验两次迭代,看两次迭代中是否改变了很多,如果在两次迭代中没怎么改变,说明算法有可能收敛。
- 另一种更常用的方法是你试图最小化的量不再发生很大的改变,也可以认为收敛。
以上的方法叫做批梯度下降法:指每一次迭代都需要遍历整个训练集合,因为你需要基于你的m个训练样本进行求和。
然而,当你有了一个很大的训练集合的时候,应该使用另外一个称为随机梯度下降的算法,也称为增量梯度下降。这个算法的好处是,在学习和改变参数的时候,只需要查看第一个训练样本来进行更新,之后再使用第二个训练样本执行下一次的更新。这样你调整参数的速度就会快得多,因为你不需要在调整之前遍历所有的数据。
对于大规模的数据集,随机梯度下降会快很多,但此算法不会精确的收敛到全局最小值,但可以无限接近全局最小值。
三、正则方程组
虽然我们已经用梯度下降法求解了求J的最小值问题,但是对于追求数学美的吴恩达来说这是远远不够的。事实上,J是一个二次函数,所以我们可以直接求得方程的解析解。下面就让我们利用偏导数和矩阵迹(tr)运算的性质来给出J最小值的解析解法。
由于一般情况下,我们要考虑一组参数,所以\theta是一个向量。那么,对于给定的一个关于\theta的函数J,我们记:
假如有一个函数f,从矩阵空间映射到实数空间
那么,当它以矩阵做为输入变量的时候,它的偏导数按如下定义:
另外一个定义是,如果A是一个方阵,可以将A的迹定义为A的对角元素之和,就是基于i对求和,即如果:
那么:
接下来,让我们再列一些关于迹运算和导数的一些结论,后面的推导过程中会用到:
所以AB的迹是一个以矩阵A为输入,以实数为输出的函数。
如果
那么
接下来,我们就可以正式推导了,我们的模型可以用向量的方式表示为:
同样的,标签信息也可以写为列向量:
这样,误差就是:
对于m个训练样本的假设,注意到:Z^TZ=\sum_i Z^{2}_{i},我们有:
这正是向量所有元素的平方和。接下来,我们就要求解最优的条件:
代入上式,我们有:
因为
所以代入上式得
所以可得
称为正规方程组。于是,我们可以最终求解得到解析表达式为:
最小二乘拟合问题,使得我们不再需要使用梯度下降这样的迭代算法