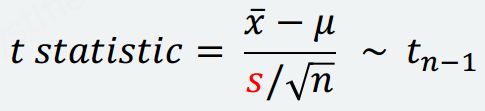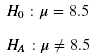感谢Dr.fish的耐心讲解和细致回答。
本次课的随堂作业如下:
同一类动物的肱骨大概具有相同的长宽比,考古学家根据这一性质来鉴定物种。考古学家发掘了41块肱骨化石,假设它们来自于同一物种,判断它们是不是物种A(已知物种A的肱骨长宽比为8.5)。取α=0.01。
进阶作业为:
使用计算机模拟方法计算课堂作业
直接上代码
# 导入分析包
import numpy as np
import pandas as pd
import scipy.stats
# 加载数据
data = [10.73, 8.89, 9.07, 9.20, 10.33, 9.98, 9.84, 9.59, 8.48, 8.71, 9.57, 9.29, 9.94, 8.07, 8.37, 6.85, 8.52, 8.87, 6.23, 9.41,
6.66, 9.35, 8.86, 9.93, 8.91, 11.77, 10.48, 10.39, 9.39, 9.17, 9.89, 8.17, 8.93, 8.80, 10.02, 8.38, 11.67, 8.30, 9.17, 12.00, 9.38]
课堂作业解题思路
- 仅有一组数据,故排除配对及双样本检验;
- 非整体数据,故排除z检验;
- 最终选择t检验。
手工计算过程:
- 设置原假设和备择假设
- 计算t统计量
1. 随堂作业部分
方法一:手工计算单样本 t 检验
# 计算 t 统计量
mean = np.mean(data)
n = len(data)
t_statistics = (mean - 8.5) / (np.std(data, ddof = 1) / np.sqrt(n))
t_statistics
# 输出结果
4.0303238468687361
# 计算 t 临界值
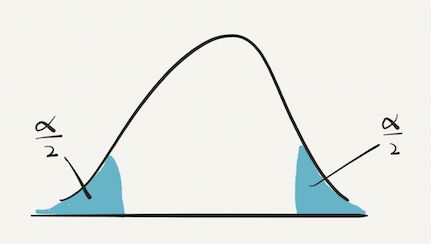
# alpha = 0.01, 双边检验,取α/2
t_critical = scipy.stats.t.isf(0.01 / 2 , df = n - 1)
t_critical
# 输出结果
2.7044592674331502
#计算 p 值验证下
p_value = scipy.stats.t.sf(t_statistics, df = n - 1) * 2 # 双边检验p值×2
p_value
# 输出结果
0.00024267304119873163
方法二:使用 scipy.stats.ttest_1samp()计算单样本 t 检验计算
t_statistics, p_value = scipy.stats.ttest_1samp(data, 8.5)
t_statistics, p_value
# 输出结果
(4.030323846868737, 0.00024267304119873163)
结论
当置信度水平α取0.01时,因为 t_statistics > t_critical (或者 p_value < α) , t统计量落在拒绝域中,所以拒绝原假设,样本不是物种A。
2. 进阶作业 - bootstrap 方法
bootstrap解题思路
bootstrap为有放回抽样,所以需要:
- 定义一个单次抽样计算P值函数
- 定义一个重复抽样并计算p值均值的函数
- 输入抽样次数
# 第一种方法 -- 公式手算
# 定义一个单次抽样并计算P值的函数,并返回单次抽样的P值
def bs_replicate_1d(data):
bs_replicate_1d = np.random.choice(data, size=len(data))
stats_mean = np.mean(bs_replicate_1d)
stats_n = len(bs_replicate_1d)
t_statistics = (stats_mean - 8.5) / (np.std(bs_replicate_1d, ddof = 1) / np.sqrt(stats_n)) #计算t统计量
stats_p = scipy.stats.t.sf(t_statistics, df = stats_n - 1) * 2
return stats_p
# 定义一个重复抽样并计算p值均值的函数,返回p值的均值
def draw_bs_reps(data, size=1):
bs_replicates = np.empty(size) # 初始一个空数组
# 进行多次重新抽样
for i in range(size):
bs_replicates[i] = bs_replicate_1d(data)
p_value = sum(bs_replicates) / size
return p_value
# 重复抽样10000次
draw_bs_reps(data, size=1000)
# 输出结果
0.0057400175854891624
# 第二种方法 -- 套函数
def bs_replicate_1d(data):
bs_replicate_1d = np.random.choice(data, size=len(data))
t_statistics, stats_p = scipy.stats.ttest_1samp(bs_replicate_1d, 8.5)
stats_p = stats_p
return stats_p
# 定义一个重复抽样并计算p值均值的函数,返回p值的均值
def draw_bs_reps(data, size=1):
bs_replicates = np.empty(size) # 初始一个空数组
# 进行多次重新抽样
for i in range(size):
bs_replicates[i] = bs_replicate_1d(data)
p_value = sum(bs_replicates) / size
return p_value
# 重复抽样10000次
draw_bs_reps(data, size=1000)
# 输出结果
0.0045788518825149857
不晓得为什么用计算机模拟算出来的p值会比用样本数据算出来的大(虽然也是落在拒绝域内吧……)