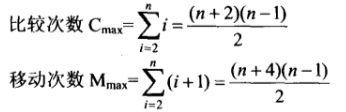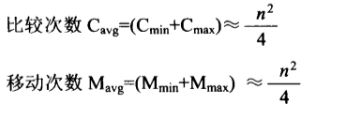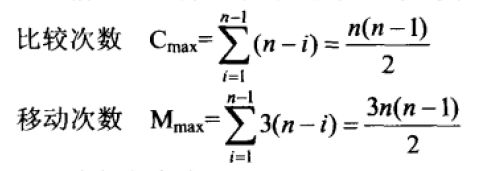前言：
2016年5月21号开始学习排序算法及其主要思想，并通过代码实现
插入排序
插入排序有两种：
- 直接插入排序
- 折半插入排序
直接插入排序
算法思想：
设有n + 1个记录，存放在数组R中，重新安排记录在数组中的存放顺序，使得按关键字有序即R[0].key <= R2.Key <= ...<=R[n].key(有序表)
- 假设待排序的记录存放在数组R[1..n]中。
- 初始时，R[1]自成1个有序区，无序区为R[2..n]。
- 从i=2起直至i=n为止，依次将R[i]插入当前的有序区R[1..i-1]中，生成含n个记录的有序区。
算法描述
直接插入排序演示图
- （1）若比较r[0] < r[i]时， j = i - 1; // 从第i个记录向前测试插入位置，用r[0]为辅助单元
- （2）若r[0].key >=r[j].key 转(4)
- （3）若r[0].key < r[j].key时，r[j + 1] = r[j]; j--；转(2) // 调整待插入位置
- (4) r[j + 1] = r[0];结束
算法实现
#include
#define N 10
void insertSort(int a[],int length) {
int j;
for (int i = 1; i <= length; i++) {
a[0] = a[i]; // 将第i个待排序记录赋值给a[0],a[0]位置为哨兵
j = i - 1; // 此时的j为哨兵的前一个元素
while (a[0] < a[j] && j >=0) { // 将第i个待排序记录同前面的i - 1 个记录比较，并为第j个记录寻找合适的插入位置
a[j + 1] = a[j];
j--;
}
a[j + 1] = a[0]; // 此时的j为合适插入位置
}
}
void main() {
int a[N + 1],i;
for (i = 1;i <= N; i++) {
scanf("%d",&a[i]);
}
insertSort(&a,N);
printf("Input Sort:\n");
for (i = 1; i < N + 1; i++) {
printf("%d",a[i]);
}
}
算法分析
时间复杂度 O(n2)
- 向有序表(R1[0].key <= R[1].key <= ... R[j - 1].key)中逐个插入记录的操作，进行了n - 1趟，每趟操作分为比较关键字和移动记录，而比较的次数和移动的次数取决于待排序列按关键字的初始排列。
- 最好情况：待排序列已按关键字正序，比较次数Cmin = n - 1 次，移动次数Mmin = 0 次
-
最坏情况：待排序列已按关键字逆序
最坏情况比较和移动次数.png -
平均情况：待排序可能出现的各种排列的概率相同
平均情况比较和移动次数.png - 直接插入算法的稳定性：是稳定的排序方法。
空间复杂度
- 需要一个辅助控件(监视哨)，辅助空间复杂度S(n)=O(1)，此算法是就地排序
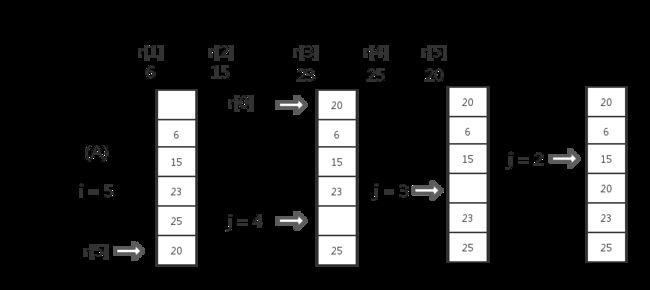
折半插入排序
直接插入排序算法渐变，且容易实现。当排序的数量n很小时，这是一种很好的排序方法。但是，通常待排序序列中的记录数量n很大，则不宜采用直接插入排序。折半插入排序（binary insertion sort）是对插入排序算法的一种改进，由于排序算法过程中，就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列，这样我们不用按顺序依次寻找插入点，可以采用折半查找的方法来加快寻找插入点的速度。
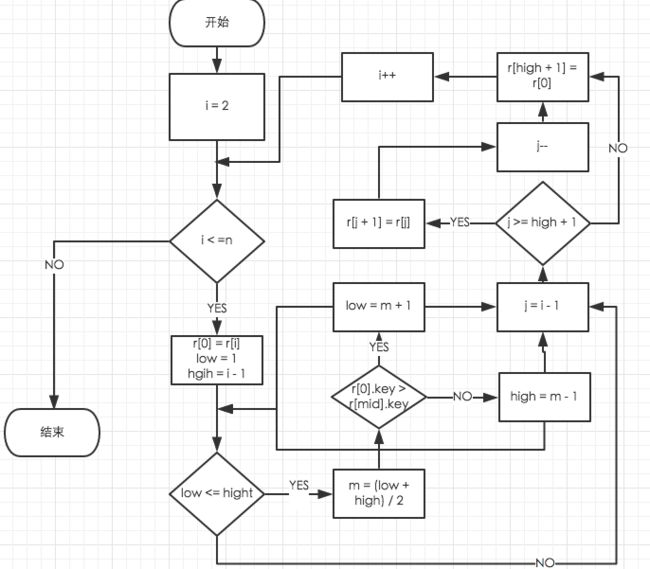
算法思想：
折半插入排序
- 向有序表中插入一个记录，插入位置是通过对有序表中记录按关键字逐个比较得到的
- 平均情况下总比较次数n2/4
- 通过二分有序表来确定插入位置，既一次比较，通过待插入记录与有序表居中的记录按关键字比较，将有序列一份为二，下次比较在其中一个有序子表中进行，将字表又一分为二。这样继续下去，直到要比较字表中只有一个记录时，比较一次就确定了插入位置
算法流程图
折半插入排序流程图
算法实现
算法分析
时间复杂度 O(n2)
折半插入排序算法是一种稳定的排序算法，比直接插入算法明显减少了关键字之间比较的次数，因此速度比直接插入排序算法快，但记录移动的次数没有变，所以折半插入排序算法的时间复杂度仍然为O(n^2)，与直接插入排序算法相同。附加空间O(1)。
- 稳定性：是稳定排序
空间复杂度
- 需要一个辅助控件，附加空间O(1)。，此算法是就地排序
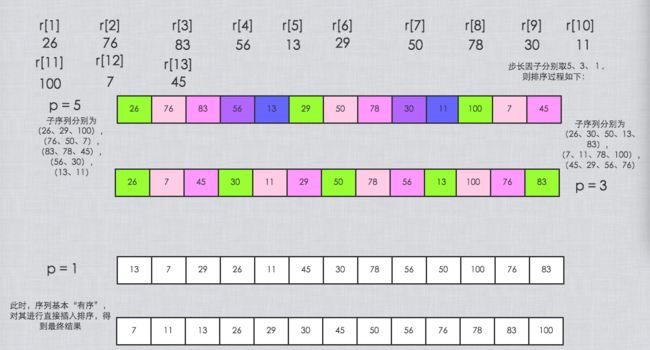
希尔排序
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。
算法思想：
希尔排序
- 选择一个步长序列t(1),t(2),...,t(k),其中t(i) > t(j), t(k) = 1。
- 按步长序列个数k，对序列进行k趟排序
- 每趟排序根据对应的步长t(i),将待排序列分隔成若干长度为m的子序列，分别对各子表进行直接插入排序。仅步长因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。
算法流程图
希尔排序流程图
p:步长因子 颜色相同：每趟排序根据对应的步长p,将待排序列分隔成若干长度为m的子序列，分别对各子表进行直接插入排序。仅步长因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。
算法实现
#include
#include
#define MAXNUM 10
void main()
{
void shellSort(int array[],int n,int t);//t为排序趟数
int array[MAXNUM],i;
for(i=0;i=i%dk)&&array[j]>temp;j-=dk)//比较与记录后移同时进行
array[j+dk]=array[j];
if(j!=i-dk)
array[j+dk]=temp;//插入
}
}
//计算Hibbard增量
int dkHibbard(int t,int k)
{
return int(pow(2,t-k+1)-1);
}
//希尔排序
void shellSort(int array[],int n,int t)
{
void shellInsert(int array[],int n,int dk);
int i;
for(i=1;i<=t;i++)
shellInsert(array,n,dkHibbard(t,i));
}
或：
#include
#define MAXNUM 10
void shellSort(int a[],int n) {
int i,j,gap,x;
gap = n / 2; // 初始步长一般为待排序文件长度的一半
while (gap > 0) { // 当步长大于0时继续排序
for ( i = gap; i < n; i++) {
// 从每个子序列的第一个位置开始比较
j = i - gap; //
while (j >= 0)
if (a[j] > a[j + gap]) { // (1) a[j]前面的元素，(2) a[j + gap]后面的元素，如果(1) > (2) 交换两个元素的位置
x = a[j];
a[j] = a[j + gap];
a[j + gap] = x;
j = j - gap; // 无符号，当前子序列的下一个结点
printf("j--!%d",j);
} else j = -1;
}
gap = gap / 2; // 步长减半
}
}
void main() {
int a[MAXNUM] = {26,76,83,56,13,29,50,78,30,11};
shellSort(a,MAXNUM);
for (int i = 0; i < MAXNUM; i++) {
printf("%d ",a[i]);
}
}
算法分析
时间复杂度 O(n2)
希尔排序是按照不同步长对元素进行，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小，插入排序对于有序的序列效率很高。所以，希尔排序的时间复杂度]会比o(n^2)好一些。
- 稳定性：是稳定排序
空间复杂度
- 需要一个辅助控件，附加空间O(1)。，此算法是就地排序
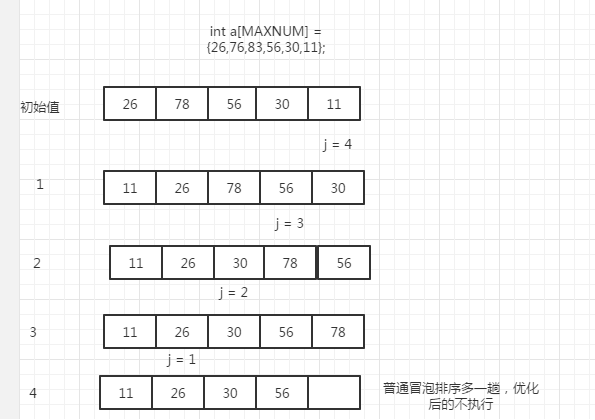
冒泡排序
冒泡排序：
- 冒泡排序
- 优化冒泡排序
算法思想：
- j = length - 1(j为数组最后一个元素)
- 若i >= j ，一趟冒泡结束
- 若a[j] < a[j - 1] 交换
- i＋＋下一趟
算法流程图
冒泡排序流程图
算法实现
#include
#define MAXNUM 10
void bubbleSort(int a[],int length) {
for (int i = 0; i < length - 1; ++i)
// 趟数，最后一趟已排序
for (int j = length - 1;j > i;--j) {
// 如果前一个元素大于后一个元素则交换
if (a[j] < a[j - 1]) {
a[j] = a[j] ^ a[j - 1];
a[j - 1] = a[j] ^ a[j - 1];
a[j] = a[j] ^ a[j - 1];
}
}
}
void main() {
int a[MAXNUM] = {26,76,83,56,13,29,50,78,30,11};
bubbleSort(a,sizeof(a) / sizeof(int));
for (int i = 0; i < MAXNUM ; i++) {
printf("%d ",a[i]);
}
}
优化冒泡排序代码：
#include
#define MAXNUM 10
void bubbleSort(int a[],int length) {
int recordSwapValue;
int swapValue = 0;
for (int i = 0; i < length - 1;i++) {
recordSwapValue = swapValue; //i... recordSwapValue的索引为有序
for (int j = length - 1; j > recordSwapValue; j--) { // R[i...recordSwapValue]或R[0...recordSwapValue]区间有序的,遍历区间由R[i...length] 缩减到[recordSwapValue..length]。
if (a[i] > a[i - 1]) {
a[j] = a[j] ^ a[j - 1];
a[j - 1] = a[j] ^ a[j - 1];
a[j] = a[j] ^ a[j - 1];
swapValue = j; // 记录交换位置的索引值
}
}
// 如果值相当，整个过程
if (recordSwapValue == swapValue) {
break;
}
}
}
void main() {
int a[MAXNUM] = {26,76,83,56,13,29,50,78,30,11};
bubbleSort(a,sizeof(a) / sizeof(int));
for (int i = 0; i < MAXNUM ; i++) {
printf("%d ",a[i]);
}
}
算法分析
时间复杂度 O(n2)
- 向有序表(R1[0].key <= R[1].key <= ... R[j - 1].key)中逐个插入记录的操作，进行了n - 1趟，每趟操作分为比较关键字和移动记录，而比较的次数和移动的次数取决于待排序列按关键字的初始排列。
- 最好情况：待排序列已按关键字正序，比较次数Cmin = n - 1 次，移动次数Mmin = 0 次
-
最坏情况：待排序列已按关键字逆序
最坏情况比较和移动次数.png -
平均情况：待排序可能出现的各种排列的概率相同
平均情况比较和移动次数
* 冒泡排序的稳定性：是稳定的排序方法。
空间复杂度 Ｏ（１）
- 需要一个辅助控件(监视哨)，辅助空间复杂度S(n)=O(1)，此算法是就地排序
快速排序
算法思想：
快速排序
* 快速排序是通过关键字、交换记录，以某个记录为界（该记录称谓支点），将待排序列分成两部分。其中一部分所有记录的关键字大于支点记录的关键字，另一部分所有记录的关键字小于支点记录的关键字。将待排序列按关键字以支点记录分成两部分的过程，称为一次划分。对各部分不断划分，直到整个序列按关键字有序，整个排序过程可以递归。
算法描述
设 1 <= p < q <= n ，r[p], r[p + 1]，...，r[q]为待排序列
- (1) low = p;high = q;
r[0] = r[low]; // 取第一个记录为支点记录，low位置暂设为支点空位 - (2) 若low = high, 支点空位确定，即为low
r[low] = r[0];
否则, low < high搜索需要交换的记录，并交换之。 - (３)若low < high 且r[high].key >= r[0].key // 从high所指向位置向前搜索，至多到low + 1 位置
high = high - 1； 转3 // 寻找r[high].key < r[0].key
r[low] = r[high]; // 找到r[high].key