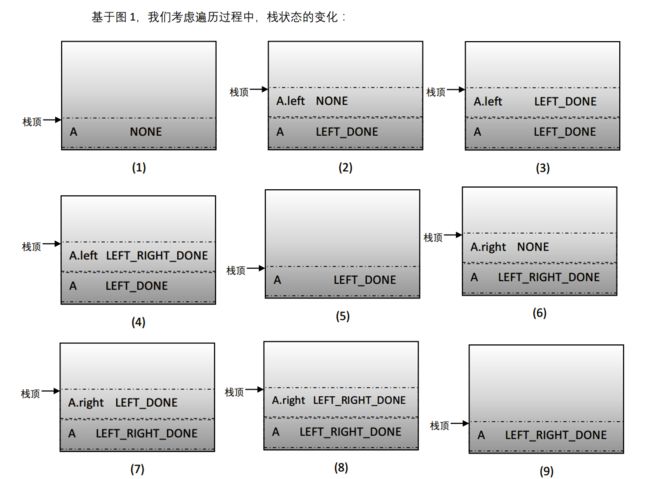
其实二叉树的3种遍历策略,无非是处理节点的时机不同:前序遍历是在遇到节点时即处理,中序是在处理完左节点后再处理,而后序是在处理完左右节点后再处理。
使用非递归方法实现时,除了记录当前的节点的访问栈,还需要记录当前节点的状态。对于每一个节点,我们用0来表示尚未处理左右子节点,1表示仅仅处理完毕左节点,2表示左右节点都处理完毕。那么,前序,中序,后序遍历的唯一不同,无非是将节点加入序列化结果集合的时机不同而已。
Node的定义如下:
class Node{
int value;
Node left;
Node right;
};
下面是通用非递归遍历的代码(前序,中序,后序):
public static final int STATE_NONE=0;//尚未处理任何一个节点
public static final int STATE_LEFT_DONE=1;//处理完左节点
public static final int STATE_LEFT_RIGHT_DONE=2;//左右节点都已经处理完
/**
*
*@param node根节点,不为null
*@param when 指明处理节点的时机,分别对应:
* STATE_NONE 前序遍历
* STATE_LEFT_DONE 中序遍历
* STATE_LEFT_RIGHT_DONE 后序遍历
*@return 对应的序列化结果
*/
public static List traverse(Node node,int when)
{
List res=new ArrayList<>();//序列化结果
Stack stackNode=new Stack<>();//保存节点的栈
Stack stackState=new Stack<>();//保存节点状态的栈
stackNode.push(node); //初始时加入根节点
stackState.push(STATE_NONE);//标记根节点为尚未处理任何子节点的状态
/*算法说明:
* 初始时放入根节点,将其标记为左右节点尚未处理的状态
* 每个循环,从栈中取出一个节点和其状态,根据其当前状态转移到下一个状
态(很显然,你可以从状态转换机的角度解读这个算法)。
* 状态转换规则: STATE_NONE-->STATE_LEFT_DONE-->STATE_LEFT_RIGTH_DONE-->弹出栈
* 伴随状态的变化,还需要相应的操作,如将左右子节点放入栈中,或者将当
前节点弹出栈;最重要的一点是,当当前节点的状态符合处理状态的要求时,就会将节点加入序列化集合。
*/
while(!stackNode.isEmpty())
{
Node n=stackNode.peek();
Integer state=stackState.peek();
if(state==when)//当前状态可处理节点
res.add(n);
//3种状态之间的转换
if(state==STATE_NONE)
{
stackState.set(stackState.size()-1,STATE_LEFT_DONE);
if(n.left!=null)
{
stackNode.push(n.left);
stackState.push(STATE_NONE);
}
}else if(state==STATE_LEFT_DONE){
stackState.set(stackState.size()-1,STATE_LEFT_RIGHT_DONE);
if(n.right!=null)
{
stackNode.push(n.right);
stackState.push(STATE_NONE);
}
}else if(state==STATE_LEFT_RIGHT_DONE){
stackNode.pop();
stackState.pop();
}
}
return res;
}
验证程序:
public static void main(String[] args) {
Node root=new Node(1);
root.left=new Node(2);
root.right=new Node(3);
root.left.left=new Node(4);
root.left.right=new Node(5);
root.right.left=new Node(6);
/* 建立了如下结构的树
1
2 3
4 5 6
*/
System.out.println("前序:"+traverse(root,STATE_NONE));//前序
System.out.println("中序:"+traverse(root,STATE_LEFT_DONE));//中序
System.out.println("后序:"+traverse(root,STATE_LEFT_RIGHT_DONE));//后序
}
输出:
前序:[1, 2, 4, 5, 3, 6]
中序:[4, 2, 5, 1, 6, 3]
后序:[4, 5, 2, 6, 3, 1]
证明
性能问题
从上面的证明中,我们可以看到栈状态的变化过程中,总共10个变化过程,但是只有3个是我们需要处理节点的状态,其他7个中间状态都是无用的。实际上,当我们知道遍历顺序时,可以优化掉不必要的中间状态。本文只是就理论层面提出了一种统一遍历的方式,实际中,我们仍然使用递归方式进行遍历。