原文
简介:什么是相关性以及它为何有用?
相关性是使用最广泛的一个-和 广泛的误解- 统计概念。在本概述中,我们提供了几种相关类型背后的定义和直觉,并说明了如何使用Python pandas库计算相关性。
术语“相关性”是指量之间的相互关系或关联。几乎在任何企业中,根据与其他企业的关系来表达一个数量是有用的。例如,当营销部门在电视广告上花费更多时,销售额可能会增加,或者电子商务网站上客户的平均购买量可能取决于与该客户相关的许多因素。通常,关联是了解这些关系并随后构建更好的业务和统计模型的第一步。
那么,为什么相关性是一个有用的指标?
- 相关性可以帮助预测一个数量与另一个数量
- 相关性可以(但通常不会,正如我们将在下面的一些示例中看到的那样)表明存在因果关系
- 相关性被用作许多其他建模技术的基本数量和基础
更正式地,相关性是描述随机变量之间关联的统计度量。存在几种用于计算相关系数的方法,每种方法测量不同类型的关联强度。下面我们总结三种最广泛使用的方法。
Types of Correlation
在我们详细了解如何计算相关性之前,重要的是引入协方差的概念。协方差是两个变量X和Y之间关联的统计量度。首先,每个变量以减去其均值为中心。这些中心分数相乘,以衡量一个变量的增加是否与另一个变量的增加相关联。最后,这些中心分数的乘积的期望值(E)被计算为关联的概要。直观地,中心得分的乘积可以被认为是矩形的区域,每个点与描述矩形的一侧的均值的距离:
如果两个变量都倾向于在同一方向上移动,我们期望将每个点(X_i,Y_i)与均值(X_bar,Y_bar)连接的“平均”矩形具有大的正对角矢量,对应于更大的正积上面的等式。如果两个变量都倾向于沿相反方向移动,我们期望平均矩形具有大且负的对角矢量,对应于上面等式中的较大负产品。如果变量不相关,那么矢量平均应该抵消- 并且总对角矢量应该具有接近0的幅度,对应于上面等式中接近0的乘积。
如果您想知道“期望值”是什么,那么它是另一种表示随机变量的平均值或平均值μ的方法。它也被称为“期望”。换句话说,我们可以写下面的等式以不同的方式表达相同的数量:
协方差的问题在于它保持变量X 和 Y的比例 , 因此可以采用任何值。这使得解释变得困难并且将协方差相互比较是不可能的。例如, Cov(X,Y)= 5.2 和 Cov(Z,Q)= 3.1 告诉我们这些对是正相关的,但很难判断X 和 Y之间的关系是否 强于Z 和Q 不看这些变量的均值和分布。这就是相关性变得有用的地方- 通过数据中某种度量变异性标准化协方差,它产生的数量具有直观的解释和一致的规模。
Pearson Correlation Coefficient
Pearson是使用最广泛的相关系数。Pearson相关性测量连续变量之间的线性关联。换句话说,该系数量化了两个变量之间的关系可以用线描述的程度。值得注意的是,虽然相关性可以有很多解释,但卡尔皮尔逊在120多年前开发的相同公式仍然是当今使用最广泛的公式。
在本节中,我们将介绍几种流行的配方和Pearson相关性的直观解释(称为ρ)。
由Pearson自己开发的原始相关公式使用原始数据和两个变量X 和 Y的平均值 :
在这个公式中,原始观察的中心是减去它们的平均值并通过标准偏差的量度重新定标。
一种不同的方式来表达相同的量是在预期值来说,意味着μ X, μ Y, 和标准偏差*σ *X, *σ *ÿ:
请注意,此分数的分子与上述协方差定义相同,因为均值和期望可以互换使用。通过标准偏差的乘积来划分两个变量之间的协方差可确保相关性始终在-1和1之间。这使得相关系数的解释变得更加容易。
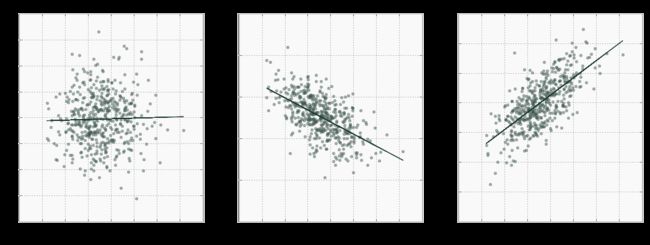
下图显示了Pearson相关性的三个例子。ρ越接近 1,一个变量的增加与另一个变量的增加相关联的越多。另一方面,ρ越接近 -1,一个变量的增加将导致另一变量的减少。注意,如果 X 和 Y是独立的,那么 ρ接近于0,但反之则不然!换句话说,即使两个变量之间存在强关系,Pearson相关性也可能很小。我们很快就会看到情况如何。
那么,我们如何解释Pearson相关性呢?
事实证明,Pearson相关性与线的斜率之间存在明显的联系。在上图中,显示了通过每个散点图的回归线。回归线是最佳的,因为它最小化了所有点与自身的距离。由于这个性质,Y和X 的回归线的斜率在 数学上等于X 和 Y之间的相关性 *, *由它们的标准偏差的比率标准化:
其中b 是Y的回归线 与 X的斜率 。
换句话说,相关性反映了两个变量之间的关联性和可变性的量。
这种与线斜率的关系有两个重要的含义:
- 它更清楚地说明为什么Pearson相关性描述了线性关系
- 它还说明了为什么相关性很重要,因此广泛用于预测建模
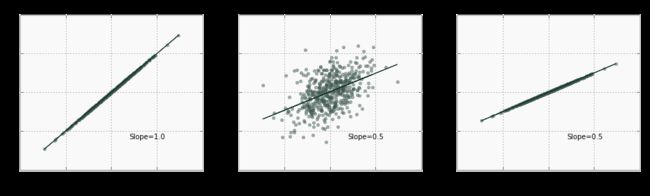
但是,请注意,在ρ的上述等式中 ,相关性不等于斜率 - 而是通过数据可变性的度量来标准化。例如,可能具有非常小的斜率,但变量之间的相关性很大。在下图中,描述这种关系的线相对平坦,但相关性为1,因为变异性s y 非常小:
请注意,到目前为止,我们还没有对X 和 Y的分布做出任何假设。唯一的限制是Pearsonρ假设两个变量之间存在线性关系。Pearson相关性依赖于平均值和标准偏差,这意味着它仅针对那些统计量是有限的分布定义,使得系数对异常值敏感。
解释Pearson相关性的另一种方法是使用确定系数,也称为R 2。虽然 ρ是无单位的,但是它的平方被解释为由X解释 的Y的方差比例 。在上面的例子中, ρ * = -0.65意味着(-0.65 2) 100 = Y的变化的42%可以用X来解释。
还有很多其他方法可以解释 ρ。如果您对相关性和向量,省略号等之间的关系感兴趣,请查看经典论文“ 查看相关系数的十三种方法 ”。
Spearman's Correlation
斯皮尔曼 等级相关系数 作为皮尔逊的特殊情况可以被定义 ρ施加到排序(排序)的变量。与皮尔逊不同,斯皮尔曼的相关性不仅限于线性关系。相反,它测量两个变量之间的单调关联(仅严格增加或减少,但不混合),并依赖于值的排序。换句话说,Spearman系数不是比较平均值和方差,而是查看每个变量的值的相对顺序。这使得适用于连续和离散数据。
Spearman系数的公式看起来非常类似于Pearson,其区别在于按行列而不是原始分数计算:
如果所有排名都是唯一的(即排名中没有关联),您还可以使用简化版本:
其中d i = rank(X i) - rank(Y i) 是每个观察的两个等级之间的差异,N是观察的数量。
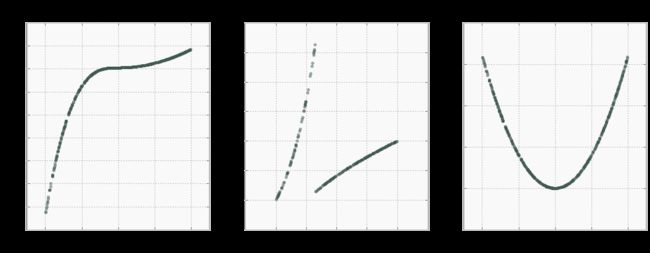
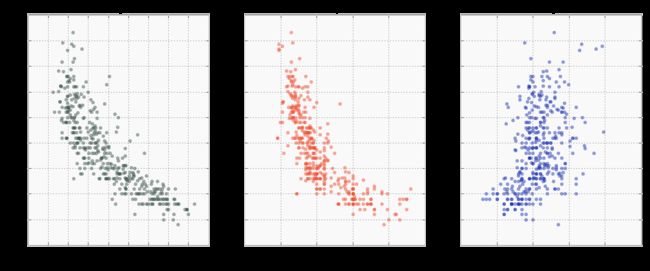
Spearman和Pearson相关性之间的差异最好用例子说明。在下图中,有三种情况,显示了两个相关系数。在第一个例子中,存在明显的单调(总是增加)和非线性关系。由于在这种情况下值的排列完全一致,因此Spearman系数为1.在这种情况下,Pearson相关性较弱,但由于关系的部分线性,它仍然显示出非常强的关联。
实施例2中的数据显示了X中的清晰基团和两个具有Y的基团的强烈但非单调的关联。在这种情况下,Pearson相关性几乎为0,因为数据非常非线性。Spearman等级相关显示弱关联,因为数据是非单调的。
最后,示例3示出了以0为中心的近似完美的二次关系。然而,由于数据的非单调,非线性和对称性质,两个相关系数几乎为0。
这些假设的例子表明,相关性决不是数据内部关系的详尽总结。如实例3中所示,弱相关或不相关并不意味着缺乏关联,甚至强相关系数也可能无法完全捕捉到关系的性质。使用可视化技术和多个统计数据摘要来获得关于变量如何相互关联的更好的图片总是一个好主意。
Kendall's Tau
我们将讨论的第三个相关系数也基于可变等级。然而,与斯皮尔曼的系数不同,肯德尔斯的τ没有考虑排名之间的差异- 只有方向性协议。因此,该系数更适合于离散数据。
形式上,肯德尔的 τ系数定义为:
例如,考虑一个由五个观察组成的简单数据集。实际上,如此少量的数据点不足以得出任何结论。但在这里,我们认为它是为了简化计算:
| X | Y | |
|---|---|---|
| a | 1 | 7 |
| b | 2 | 5 |
| c | 3 | 1 |
| d | 4 | 6 |
| e | 5 | 9 |
一致对(*x 1,y 1),(x 2,y *2)是其中列重合的值对: *x *1 < *x *2且 *y *1 < *y *2或 *x *1 > *x *2且 *y *1 > y 2。在我们的迷你示例中,行d和e中的(4,6)和(5,9)是一致的对。不一致对将是不满足该条件的对,例如(1,7)和(2,5)。计算τ的分子 ,我们比较数据集中所有可能的对并计算一致对的数量; 在这种情况下6:
- (1,7)和(5,9)
- (2,5)和(4,6)
- (2,5)和(5,9)
- (3,1)和(4,6)
- (3,1)和(5,9)
- (4,6)和(5,9)
和不和谐的对:
- (1,7)和(2,5)
- (1,7)和(3,1)
- (1,7)和(4,6)
- (2,5)和(3,1)
Kendall的的分母τ是对可能的组合,从而确保只数τ 1和-1之间变化。对于五个数据点,存在5 * 4/2 = 10种可能的组合,在该示例中使得τ =(6-4)/ 10 = 0.2。肯德尔的相关性对于离散数据特别有用,其中数据点的相对位置对于它们之间的差异更为重要。
# fake kendall
k = pd.DataFrame()
k['X'] = np.arange(5)+1
k['Y'] = [7, 5,1, 6, 9]
print k.corr(method='kendall')
XY X 1.0 0.2 Y 0.2 1.0
PANDAS计算的相关性
# pandas provide a convenient method for highlighting
# mpg_data.drop(['m
下面,我们将展示如何使用Python库计算示例问题的相关性。我们将使用加州大学欧文分校的车辆燃油效率数据集。让我们说有兴趣看看哪种车辆特性可以帮助解释车辆的燃油消耗(mpg)。我们首先从UCI在线数据存储库中读取数据集并检查前几行。数据集文档指出一个特殊字符用于缺失值(?),它可以用作pandas read_csv()函数的一个参数:
import pandas as pd
path = 'http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data'
mpg_data = pd.read_csv(path, delim_whitespace=True, header=None,
names = ['mpg', 'cylinders', 'displacement','horsepower',
'weight', 'acceleration', 'model_year', 'origin', 'name'],
na_values='?')
在检查数据集时,我们看到horsepower有六个缺失值,大熊猫的相关方法将自动丢弃。由于缺失值的数量很少,因此对于我们的说明性示例,此设置是可接受的。但是,请始终确保删除缺失值适合您的用例。如果不是这种情况,则存在许多用于填充和处理缺失值的现有方法,例如简单的平均插补。
mpg_data.info()
RangeIndex: 398 entries, 0 to 397
Data columns (total 9 columns):
mpg 398 non-null float64
cylinders 398 non-null int64
displacement 398 non-null float64
horsepower 392 non-null float64
weight 398 non-null float64
acceleration 398 non-null float64
model_year 398 non-null int64
origin 398 non-null int64
name 398 non-null object
dtypes: float64(5), int64(3), object(1)
memory usage: 28.1+ KB
pandas提供了一种方便的单行方法,corr()用于计算数据帧列之间的相关性。在我们的燃油效率示例中,我们可以mpg通过将方法传递到特定列来检查较重的车辆是否倾向于降低:
mpg_data['mpg'].corr(mpg_data['weight'])
-0.8317409332443354
正如预期的那样,车辆weight和车辆之间似乎存在强烈的负相关关系mpg。但是horsepower或者displacement呢?方便的是,pandas可以快速计算数据帧中所有列之间的相关性。用户还可以指定相关方法:Spearman,Pearson或Kendall。如果未指定方法,则默认使用Pearson。在这里,我们删除模型年份和原始变量,并计算数据框的所有剩余列之间的Pearson相关性:
in[]:
# pairwise correlation
mpg_data.drop(['model_year', 'origin'], axis=1).corr(method='spearman')
out[]:
| MPG | 汽缸 | 移位 | 马力 | 重量 | 促进 | |
|---|---|---|---|---|---|---|
| MPG | 1.000000 | -0.821864 | -0.855692 | -0.853616 | -0.874947 | 0.438677 |
| 汽缸 | -0.821864 | 1.000000 | 0.911876 | 0.816188 | 0.873314 | -0.474189 |
| 移位 | -0.855692 | 0.911876 | 1.000000 | 0.876171 | 0.945986 | -0.496512 |
| 马力 | -0.853616 | 0.816188 | 0.876171 | 1.000000 | 0.878819 | -0.658142 |
| 重量 | -0.874947 | 0.873314 | 0.945986 | 0.878819 | 1.000000 | -0.404550 |
| 促进 | 0.438677 | -0.474189 | -0.496512 | -0.658142 | -0.404550 | 1.000000 |
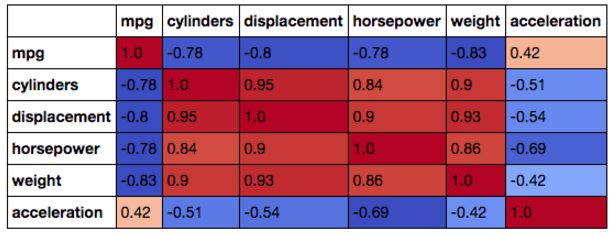
pandas还支持突出显示表的方法,因此更容易看到高和低相关性。了解数据中可能存在的相关性非常重要,尤其是在构建回归模型时。强相关预测因子,称为多重共线性的现象,将导致系数估计不太可靠。下面是一个在我们的数据上计算Pearson相关性并使用颜色渐变来格式化结果表的示例:
odel_year', 'origin'], axis=1).corr(method='pearson').style.format("{:.2}").background_gradient(cmap=plt.get_cmap('coolwarm'), axis=1)
最后,目测检查之间的关系mpg,weight,horsepower,和acceleration,我们就可以绘制这些值并计算皮尔逊和斯皮尔曼系数。手头的数据集包含少于400个点,可以在散点图上轻松显示。如果您要处理更大的数据集,请考虑首先采集数据样本以加快流程并生成更易读的图表。
在这种情况下,斯皮尔曼系数比皮尔逊更高horsepower和weight,由于关系是非线性的。因为acceleration,两个系数都很接近,因为关系没有明确定义:
# plot correlated values
plt.rcParams['figure.figsize'] = [16, 6]
fig, ax = plt.subplots(nrows=1, ncols=3)
ax=ax.flatten()
cols = ['weight', 'horsepower', 'acceleration']
colors=['#415952', '#f35134', '#243AB5', '#243AB5']
j=0
for i in ax:
if j==0:
i.set_ylabel('MPG')
i.scatter(mpg_data[cols[j]], mpg_data['mpg'], alpha=0.5, color=colors[j])
i.set_xlabel(cols[j])
i.set_title('Pearson: %s'%mpg_data.corr().loc[cols[j]]['mpg'].round(2)+' Spearman: %s'%mpg_data.corr(method='spearman').loc[cols[j]]['mpg'].round(2))
j+=1
plt.show()
相关与因果关系
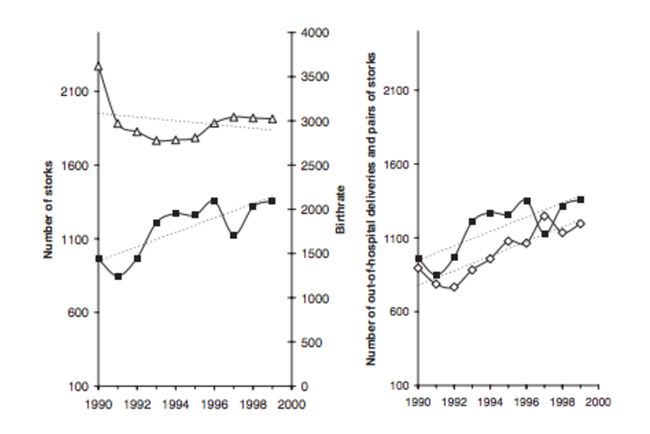
我们的燃油效率示例中的变量之间的关系非常直观,可通过车辆力学解释。然而,事情并不总是那么简单。众所周知,相关性并不意味着因果关系,因此,任何强相关都应该被认为是批判性的。例如,德国研究人员在这篇幽默的论文中使用了相关概念 来支持婴儿由鹳提供的理论。该图显示了鹳的数量与婴儿分娩之间的相关性:
左图显示鹳数量(黑线)的增加趋势和临床分娩数量的减少趋势。另一方面,右侧的图表显示,许多院外分娩(白色方形标记)遵循鹳数量增加的模式。通过观察这些系列之间的相关性,作者提出,院外分娩的增加与鹳数量的增加以及医院分娩的同时减少表明德国越来越多的婴儿正在通过鹳分娩。
当然,这是一个愚蠢的例子。尽管如此,它表明了一个重要的观点:虚假的统计关联可以在很多数量中找到,仅仅是因为偶然。
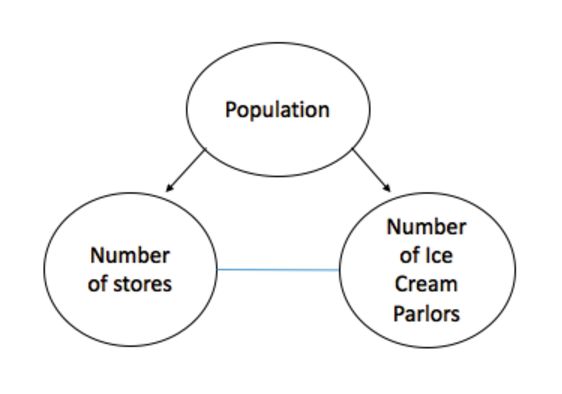
通常,由于一些未观察到的变量,关系可能通过高相关性似乎是因果关系。例如,一个城市的杂货店数量可以与冰淇淋奶油的数量密切相关。但是,这里有一个明显的隐藏变量- 城市的人口规模:
这些示例显示了关联如何只是一个数据汇总统计数据,它决不会告诉数据中关系的完整故事。
最后的评论
本概述是相关类型和解释的入门读物。我们引入了三种流行的相关方法,并演示了如何使用它们进行计算pandas。在许多应用中,相关性是一个有用的数量,特别是在进行回归分析时。虽然这里列出的方法被广泛使用并涵盖了大多数用例,但是这里没有涉及其他关联度量,例如二进制数据或互信息的phi系数。
参考
Rodgers,JL,&Nicewander,WA(1988)。十三种观察相关系数的方法。美国统计学家,42(1),59-66。
Lichman,M。(2013)。UCI机器学习库[ http://archive.ics.uci.edu/ml ]。加利福尼亚州欧文市:加州大学信息与计算机科学学院。
Hofer,T.,Przyrembel,H。,&Verleger,S。(2004)。鹳理论的新证据。儿科和围产期流行病学,18(1),88-92。