神经网络第2部分: 设置数据和损失

神经网络第2部分: 设置数据和损失
- 1.数据预处理
  - 0均值化
  - 标准化
  - 主成份分析(PCA)
  - 小结
- 2.权值初始化
  - 0值初始化
  - 随机小数值初始化
  - Bias初始化
  - 小结
- 3.正则化
  - L2范数
  - L1范数
  - Max norm constraints
  - 随机失活（Dropout）
  - 正向传递中的噪声
  - Bias正则化
  - 小结
- 4.损失函数（Loss functions）
  - 分类
  - 问题：大量的类别
  - 属性分类
  - 回归（Regression）
  - 小节
- 总结

1.数据预处理

0均值化

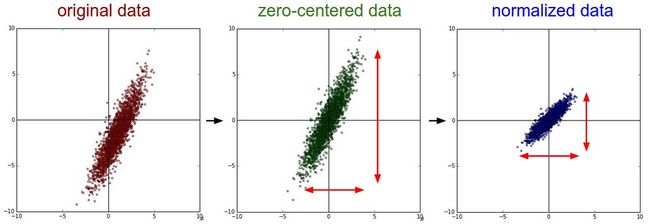
0均值化是将数据调整为以0为中心的处理。

最常见的数据预处理，将数据Xi中每一维的数据都减去这一维的均值，代码为：X -= np.mean(X, axis = 0)。

对于图片数据来说，因为X中的值都在0与255之间，可以直接减去整个整个X的均值，代码为：X -= np.mean(X)。

标准化

标准化是将数据按比例缩放，使之落入一个小的特定区间。

一种方法是将已经0均值化的数据除以它的标准差，代码为：X /= np.std(X, axis = 0)，这个处理将数据分布调整到-1和1之间。

标准化只对每一个维度范围不一样数据有意义，对图片这种每一个像素值都在0到255的数据，不是必须的处理。

image

左图是原始数据，中图是0均值化后的数据，右图为标准化后的数据。

主成份分析(PCA)

主成分分析主要用于数据降维，保留数据的主要特征。

PCA的处理流程为：

对数据X进行0均值化
计算X的协方差矩阵
对协方差矩阵进行奇异值分解（SVD）
使用特征矩阵对数据X进行降维

具体代码大致如下：

# 假设X的shape为 N by D
X -= np.mean(X, axis = 0)           # 0均值化（必须）
cov = np.dot(X.T, X) / X.shape[0]   # 计算协方差矩阵
U,S,V = np.linalg.svd(cov)          # 奇异值分解，S为奇异向量
Xrot_reduced = np.dot(X, U[:,:144]) # 将X降到144维

矩阵U的列是X的标准正交的特征向量，可以把他们看作基向量。并且这些特征向量已经按特征值从大到小排序，我们只需要取指定的前n个特征向量（上述代码n取144）并将X映射过去，就能将X降为相应的n维数据（即Xi由D维降到n维）。

和PCA类似，还有一种预处理白化，它是将X映射到完整的U上并进行标准化（归一化），代码如下：

Xrot = np.dot(X, U) # decorrelate the data
Xwhite = Xrot / np.sqrt(S + 1e-5) #加1e-5为了防止除0

白化有一个缺点，它将所有特征都变得同样重要，这样会大幅扩大噪声。

[图片上传失败...(image-ab443-1533216356449)]
左图是原始数据，中图是投影到U上后的数据，右图为白化后的数据。

image

上述是用CIFAR-10的图片做实验进行PCA和白化，从左到右：

原始图片，3072维（32像素宽，32像素高，3通道）
U中的前144个特征向量，即U[:,:144],其中每一列表示为一张图片
PCA降维后还原的图片，代码为Xrot.dot(U.T[:144,:])，3072维
白化后的图片，低频部分被忽略，高频部分被放大

小结

在CNN中必要的预处理是0均值化，注意0均值化对于训练集、验证集和测试集都是减训练集的均值。

2.权值初始化

在训练神经网络之前，我们需要初始化权值矩阵W，而W取什么值是需要考虑的问题。

0值初始化

将权值矩阵全部初始化为0是一个误区，如果每个神经元计算出相同的输出，在BP时也会计算出同样的梯度。另外，对于使用ReLU作为激活函数的隐层，输出为0且BP时梯度也都为0，这意味着所有非输入层神经元都死了，学习失败。

随机小数值初始化

我们还是希望用接近0的小数值来初始化权值W，一般采用高斯分布的随机数，代码为W = 0.01* np.random.randn(D,H)，W的均值为0。注意不能用太小的值来初始化W，过小的W会使BP时计算的梯度太小而导致梯度消失。

用1/sqrt(n)来校正方差。上述方法的一个问题随机初始化的神经元的输出的方差随着输入的增加而增加，所以我们将权值除以相应神经元的输入个数（证明参见原文），网络中的所有神经元都会有相同的输出分布，代码为：w = np.random.randn(n) / sqrt(n)。近期还有研究表明在特定的情况下ReLu神经元建议用w = np.random.randn(n) / sqrt(2.0/n)作为初始权值。

Bias初始化

还记得Bias吗？Bias一般初始化为0，实践证明初始化为0.01之类的有时结果很糟。

小结

建议使用ReLu激活并使用w = np.random.randn(n) / sqrt(2.0/n)进行权值初始化。

另外，最近一项研究可以减轻很多神经网络初始化带来的麻烦，具体内容见Batch Normalization。

3.正则化

正则化是一种惩罚模型复杂性的方法，一般用来控制权值W的大小和分布，防止网络训练过拟合。

L2范数

L2范数是最常用的正则化处理，Loss函数加上 $\frac{1}{2} \lambda w^2$ 可以直接对权值 $w$ 进行平方量级的惩罚。系数之所以为 $\frac{1}{2}$ ，是因为 $\frac{1}{2} \lambda w^2$ 对于 $w$ 的梯度可以简单表示为 $\lambda w$ 。L2范数对陡峭的权值向量进行很重的惩罚并有利于获得比较分散的权值向量。

L1范数

L1范数也是相比较常用的正则化处理，Loss函数加上 $\lambda \mid w \mid$ 一样可以对权值 $w$ 进行惩罚，并有利于获得比较稀疏的权值向量。使用L2范数一般会获得比L1范数更分散且值较小的权值向量，所以L2范数一般比L1范数性能好。

Max norm constraints

Max norm constraints是一种约束权值向量绝对值上限的方式，并用投影梯度下降确保这个约束。在实践中，像往常一样更新参数，然后强制权值 $w$ 满足 $\Vert w \Vert_2 < c$ ， $c$ 一般为3或4。这种方法的性质是即使学习率设置很大也不会发生数值爆炸，因为参数更新永远在一定范围内。

随机失活（Dropout）

随机失活是一种Srivastava在Dropout: A Simple Way to Prevent Neural Networks from Overfitting中提出的简单且非常有效的正则化方法，它对其它方法（L1，L2，Maxnorm）进行补充。在训练时，随机失活保持神经元以概率 $p$ （超参数）激活,否则让其死亡（设为0）。

[图片上传失败...(image-ed5518-1533216356449)]

上图是从论文中摘下来的，它描述了这种思想。在训练中，随机失活可以理解为从全连接的神经网络中进行取样，在输入数据的基础上只更新被取样的网络。在测试的时候，不采用随机失活，可以理解为是对所有子网络的指数级ensemble（将在下一部分介绍）作一个平均预测。

Vanilla的一个三层网络的随机失活代码实现如下：

""" Vanilla Dropout: 这不是建议的实现方式 (具体的往下看) """

p = 0.5 # 随机失活的概率

def train_step(X):
  """ X contains the data """
  
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = np.random.rand(*H1.shape) < p # 第一隐层输出的失活掩码
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = np.random.rand(*H2.shape) < p # 第二隐层输出的失活掩码
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)
  
def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) * p # 将第一隐层输出缩放
  H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # 将第二隐层输出缩放
  out = np.dot(W3, H2) + b3

上述代码的train_step函数在第一个隐层和第二个隐层的输出上进行了两次随机失活，当然对输入层的输出X进行随机失活也是可以的。反向传播保持不变，但是当然不得不考虑正向生成的掩码U1和U2。（如何考虑？）

关键是要注意预测函数predict并没有使用任何随机失活，但是将两个隐层的输出按比例 $p$ 缩放了。这一点很重要，因为在测试阶段所有的神经元是看得到所有的输入的而训练阶段不是，所以我们希望测试阶段的输出和训练阶段的输出保持一致。

为了不在关键的测试阶段缩放数据，一般采用反向随机失活（inverted dropout），即在训练阶段使用随机失活后就立即反向缩放数据来还原输出量，代码如下：

""" 
Inverted Dropout: 这才是建议的实现方式
在训练阶段反向缩放数据，不用动测试阶段的代码。
"""

p = 0.5 # 随机失活的概率

def train_step(X):
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = (np.random.rand(*H1.shape) < p) / p # 第一隐层失活，注意放大了1/p!
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = (np.random.rand(*H2.shape) < p) / p # 第一隐层失活. 注意放大了1/p!
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)
  
def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) # 这里没有缩放了！
  H2 = np.maximum(0, np.dot(W2, H1) + b2) # 这里没有缩放了！
  out = np.dot(W3, H2) + b3

正向传递中的噪声

随机失活属于网络正向传递的随机行为中的一般方法中的一种，经过测试，通过这种方法噪声会被边缘化。DropConnect是这个方面的另一种方法，它在正向传递时用随机数的掩码代替随机失活中的0掩码。在CNN中有很多类似的方法，包括随机采样池化（stochastic pooling）等，将在后续章节介绍。

Bias正则化

还记得Bias吗？我们一般不正则化Bias，因为它不与数据交互。

小结

一般最最常用的正则化方式是单独使用L2范数，然后在每层使用 $p = 0.5$ 的随机失活， $p$ 可以使用验证集调整。

4.损失函数（Loss functions）

损失函数是一个监督学习的问题，用来衡量预测和真实标签的匹配度。整体的数据损失是每个样本损失的均值， $L = \frac{1}{N} \sum_i L_i$ ，N是训练样本数。我们将输出层的激活函数简写为 $f = f(x_i; W)$ ，接下来我们讨论一些问题：

分类

假设数据集中每个样本只有一个正确的标签，一个最常用的损失函数是SVM分类器使用的铰链损失（hinge loss）：
$L_i = \sum_{j\neq y_i} \max(0, f_j - f_{y_i} + 1)$
有些报道称用平方铰链损失（squared hinge loss） $\max(0, f_j - f_{y_i} + 1)^2$ 具有更好的性能。另一种常用的损失函数是Softmax分类器使用的交叉熵损失（cross-entropy loss）：
$L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right)$

问题：大量的类别

当标签种类非常多（例如字典里的词数或者ImageNet中的22000个图片类别）时，可能需要用到分层Softmax(Hierarchical Softmax)。分层Softmax将所有类别标签分解到一棵二叉树中，每一个类别标签表示为树上的一条路径，详细的内容见将其应用于Word2Vec的论文。

属性分类

输出向量不是含有每个样本的单个的类别标签，而是含有每个样本中所具有的多个属性标签，比如说Instagram上的一张图片含有多个关键字。一种明智的做法是为每一个属性创建一个独立的二分类器：
$L_i = \sum_j \max(0, 1 - y_{ij} f_j)$
上式中 $j$ 为属性种类， $y_{ij}$ 为标签，表示 $i$ 样本是否具有 $j$ 属性，取值为+1或-1。 $f_j$ 为预测值，正值表示预测具有 $j$ 属性，否则不具有 $j$ 属性。

另一种可选的方法是为每个属性单独的训练一个逻辑回归（logistic regression）分类器。一个二元逻辑回归分类器只拥有两个类别（0,1），然后计算类别1的概率：
$P(y = 1 \mid x; w, b) = \frac{1}{1 + e^{-(w^Tx +b)}} = \sigma (w^Tx + b)$
因为类别1和类别0的概率之和为1，所以类别0的概率为 $P(y = 0 \mid x; w, b) = 1 - P(y = 1 \mid x; w,b)$ 。当 $\sigma (w^Tx + b) > 0.5$ 或 $w^Tx +b > 0$ 时样本为正例，即分类为1。损失函数为：
$L_i = - \sum_j y_{ij} \log(\sigma(f_j)) + (1 - y_{ij}) \log(1 - \sigma(f_j))$
损失函数对 $f$ 求导结果非常简单 $\partial{L_i} / \partial{f_j} = y_{ij} - \sigma(f_j)$ 。

回归（Regression）

回归是预测连续实值的任务，比如预测房价。在这种任务中，损失函数一般计算预测值和实际值差值的L2范数平方或L1范数。使用L2范数平方的损失函数表示为：
$L_i = \Vert f - y_i \Vert_2^2$
之所以用L2范数平方是因为求梯度简单。注意回归问题比分类问题难优化的多，处理回归问题应该最先考虑是否能转化为分类问题。

小节

在每类任务中采用最常用的损失函数

总结

对数据X进行0均值化处理
使用w = np.random.randn(n) * sqrt(2.0/n)初始化权值W，n为输入变量个数
使用L2范数正则化并采用反向随机失活
使用batch normalization
在每类任务中采用最常用的损失函数

CS231n 神经网络第2部分: 设置数据和损失

神经网络第2部分: 设置数据和损失

1.数据预处理

0均值化

标准化

主成份分析(PCA)

小结

2.权值初始化

0值初始化

随机小数值初始化

Bias初始化

小结

3.正则化

L2范数

L1范数

Max norm constraints

随机失活（Dropout）

正向传递中的噪声

Bias正则化

小结

4.损失函数（Loss functions）

分类

问题：大量的类别

属性分类

回归（Regression）

小节

总结

你可能感兴趣的:(CS231n 神经网络第2部分: 设置数据和损失)

CS231n 神经网络 第2部分: 设置数据和损失

神经网络 第2部分: 设置数据和损失

1.数据预处理

0均值化

标准化

主成份分析(PCA)

小结

2.权值初始化

0值初始化

随机小数值初始化

Bias初始化

小结

3.正则化

L2范数

L1范数

Max norm constraints

随机失活（Dropout）

正向传递中的噪声

Bias正则化

小结

4.损失函数（Loss functions）

分类

问题：大量的类别

属性分类

回归（Regression）

小节

总结

你可能感兴趣的:(CS231n 神经网络 第2部分: 设置数据和损失)

CS231n 神经网络第2部分: 设置数据和损失

神经网络第2部分: 设置数据和损失

你可能感兴趣的:(CS231n 神经网络第2部分: 设置数据和损失)