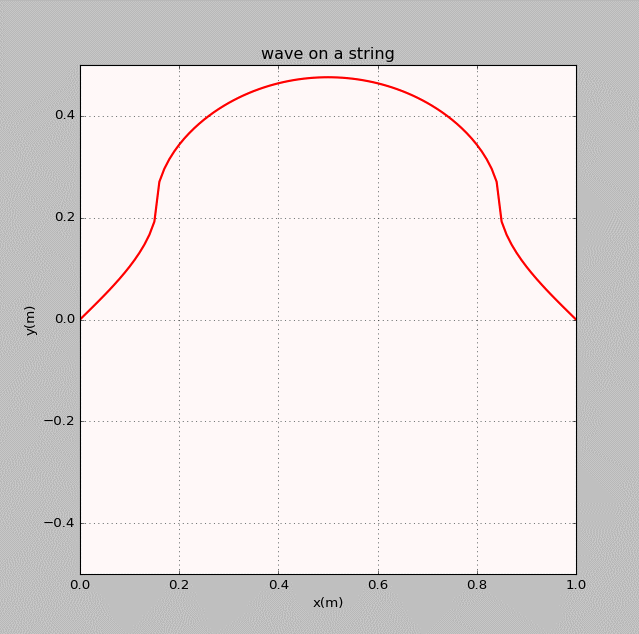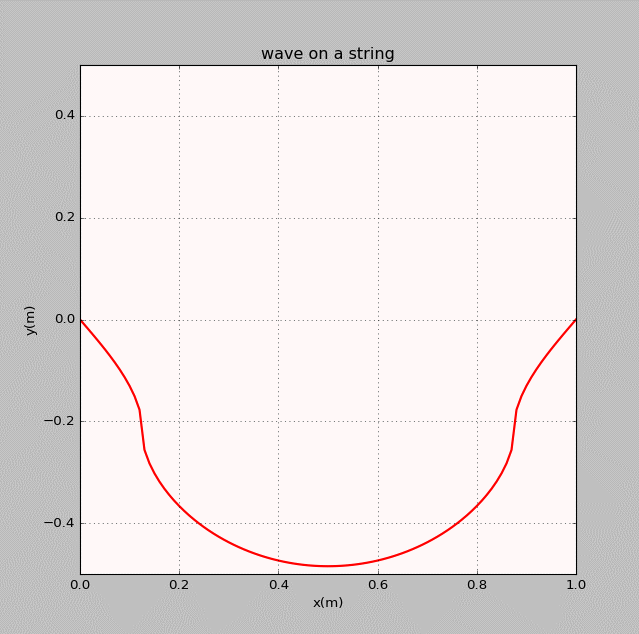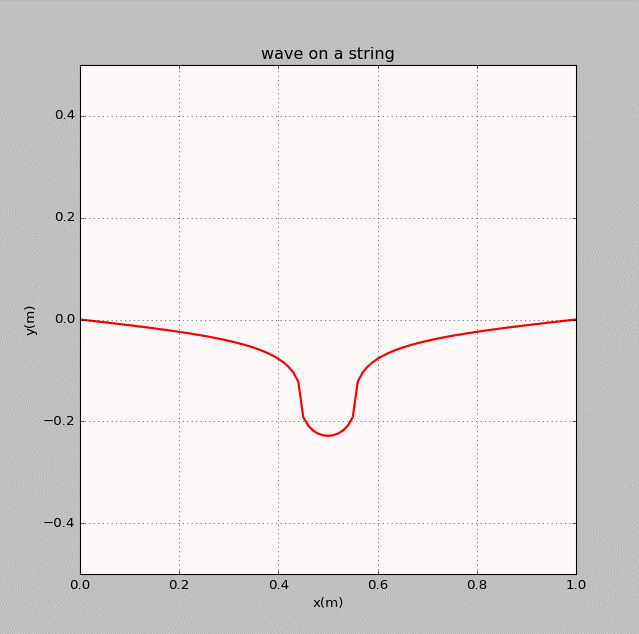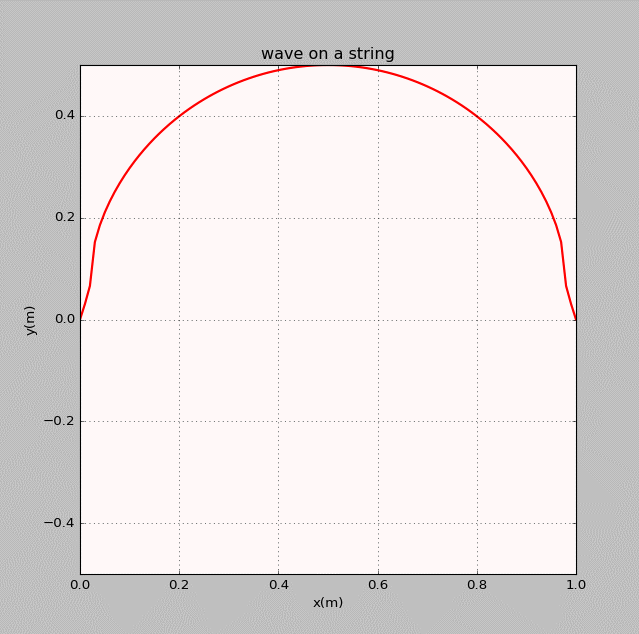
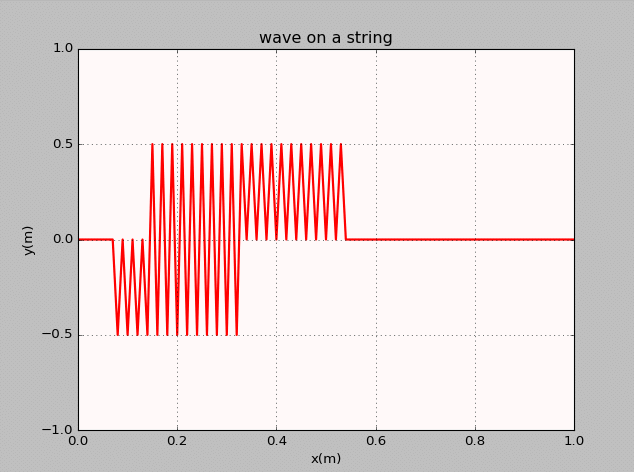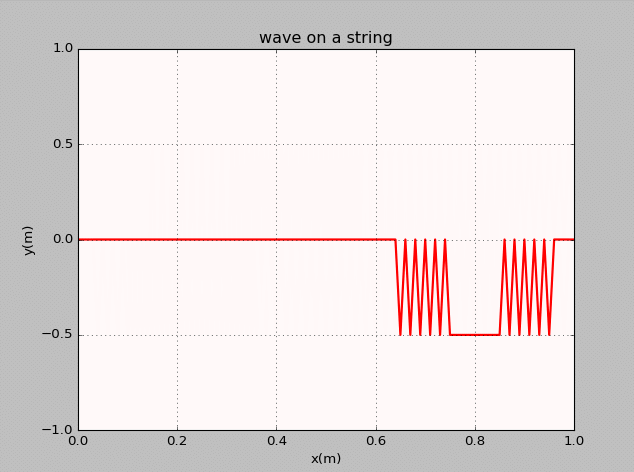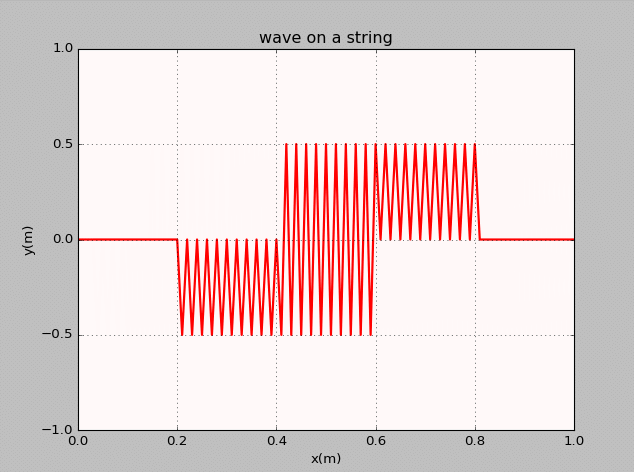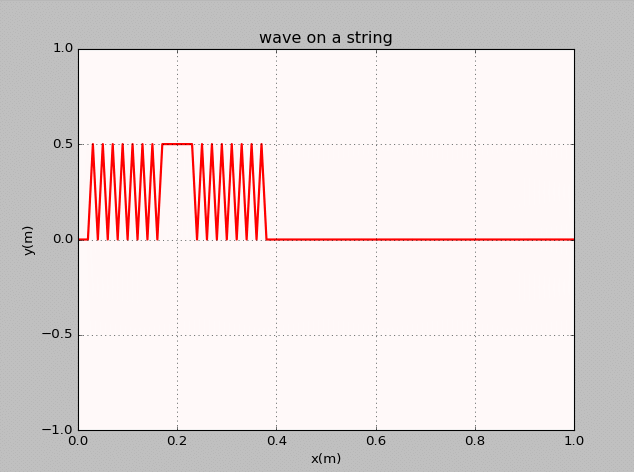
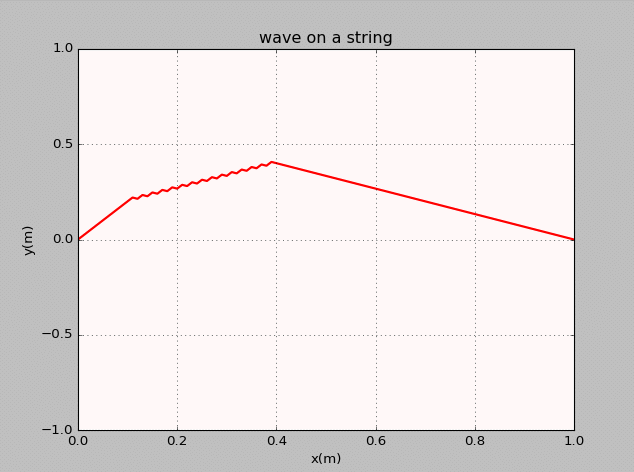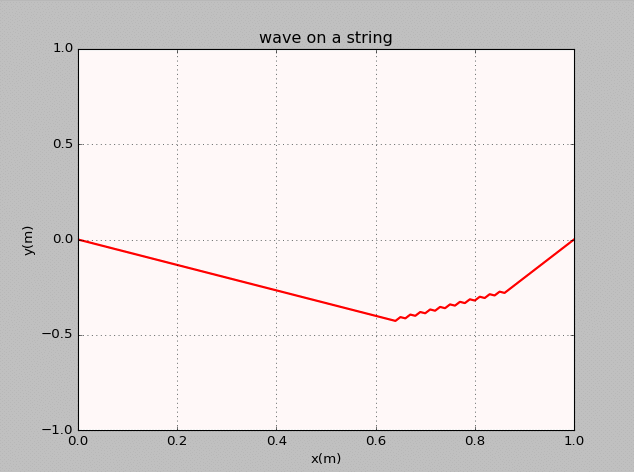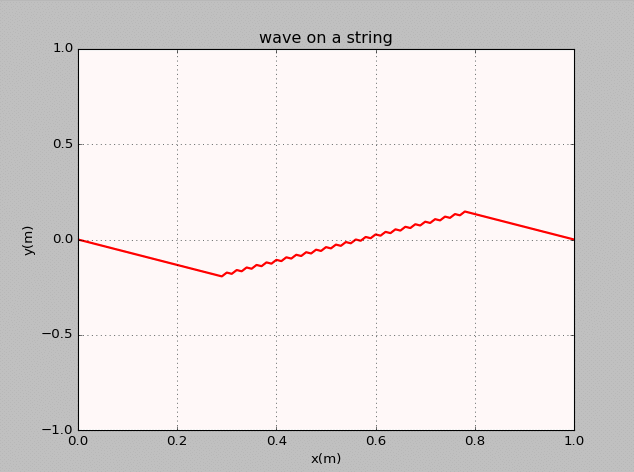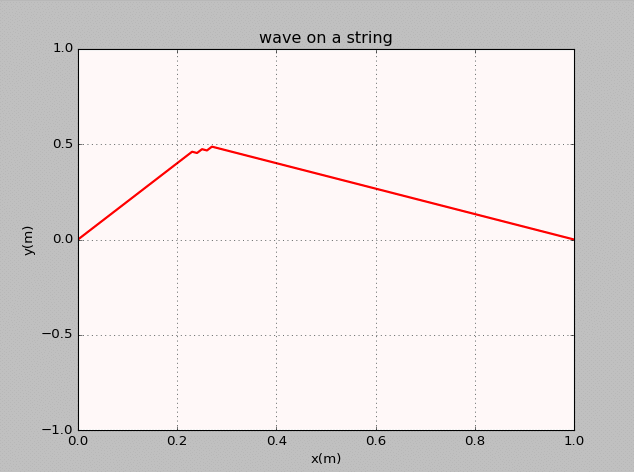
The thirteenth homework-Waves

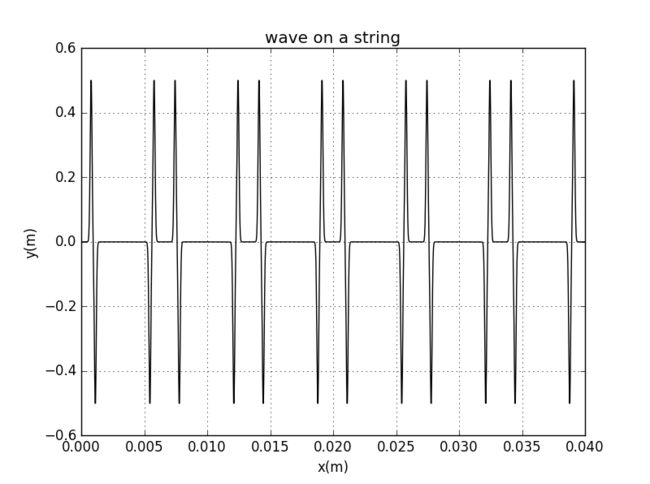
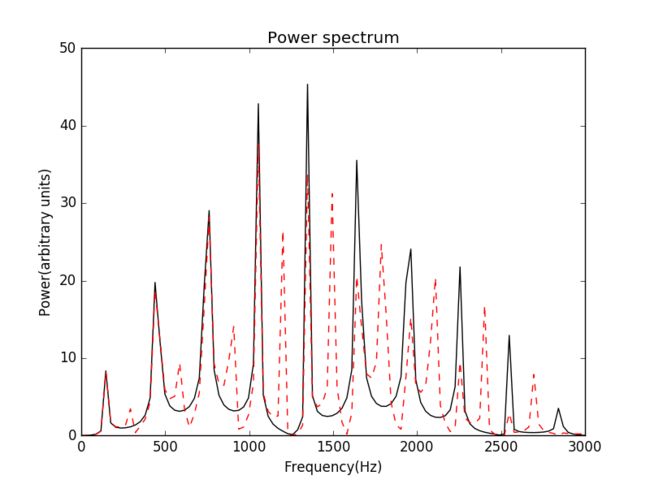
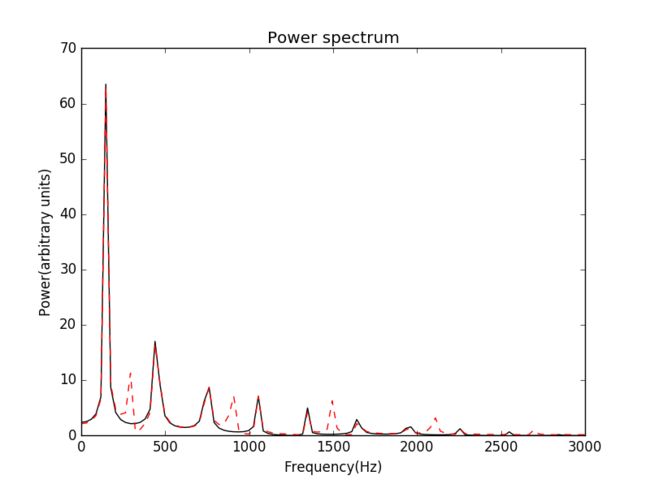
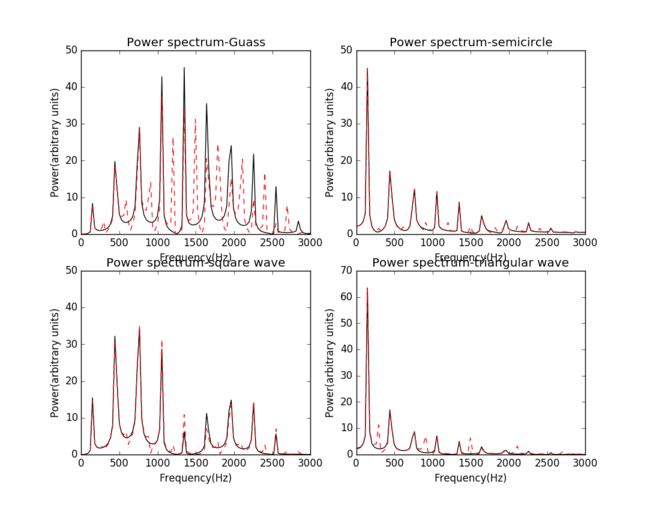
谭善

2014301020106

---

---

1. Abstract

---

---

In physics, a wave is an oscillation accompanied by a transfer of energy that travels through a medium (space or mass). Frequency refers to the addition of time. Wave motion transfers energy from one point to another, which displace particles of the transmission medium–that is, with little or no associated mass transport. Waves consist, instead, of oscillations or vibrations (of a physical quantity), around almost fixed locations. Here, I will talk about some specific examples about waves, such as waves on the string.

Question 6.12

Guassian innitial string displacements are convenient for the calculations of this seciton, but are not very realistic. When a real string, such as a guitar string, is plucked, the initial string displacement is more accurately described by two straight lines that start at the ends of the string (we assume fixed ends) and end at the excitation point, as illustrated in Figure 6.4. Compare the power spectrum for a string excited in this manner with the results found above for a Gaussian initial wavepacket.

---

---

2. Background and Introduction

---

---

The central equation of wave motion is

If we assume that the string displacement is small, so that the angles \theta_i are also small, we can write the equation of the motion of segment i as

and then use a finite difference approximation for the angles

We obtain

We have already derived the needed expression for the second partial derivative, and inserting it into the wave equation, yields

Rearranging it, we have

In our homework, we just set r=1, so

We have taken the initial string profile to be

---

---

3. Body Content

---

---

• First, we consider a kind of simple situation. While the initial displacement has a Gaussian profile, it quickly splits into two separate wavepackets, or pluses, which propagate in oppose directions along the string.

  
  
  

---

• If we give two Gaussian profile, we will see two peaks split into four peaks, and lower peaks will not change higher peaks.

  
  
  

---

• Now, we can consider some another interesting situations, such as semicircle wave, square wave, and two different triangular wave.

• Semicircle wave

• Square wave

• Triangular wave 1

• Triangular wave 2

---

• Signal from a vibrating string. The string was excited with a Guassian initial pluck centered at the middle of the string, and the displacement a distance 5 percent from one end was recorded.

  
  
  

• Also, we can consider two Gaussian profile, semicircle profile, square profile and triangular profile.

  
  
  

---

• The dotted curve is the power spectrum obtained when the string was excited 5 percent from its center. (One Guassian profile)

  
  
  

• Triangualr wave2

  
  
  

• Some situations including one Guassian profile, semicircle profile, square profile and triangular profile.

  
  
  

---

---

4. Conclusion

---

---

• We have taken a flood of initial profile into consideration, and these examples are considerably classical.

• There isn't any interference between two different waves in the same string.

• String singnal has told us that the period of the wave.

• When we the string was excited some distance from its center, we will find that there would be more peaks in the power spectrum.

---

---

5. Reference and Acknowledgement

• Computational Physics (Second Edition), Nicholas J. Giordano, Hisao Nakannishi.

• Yuqiao Wu

• Wikipedia-Waves

---

---

6. Code

• Code1
• Code2
• Code3