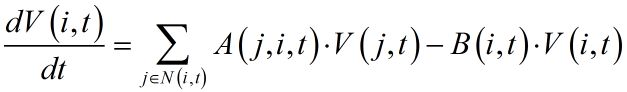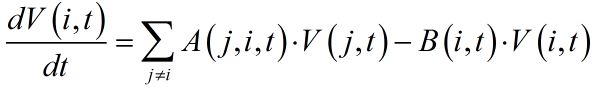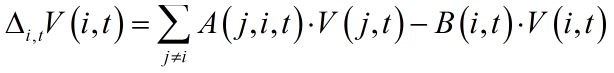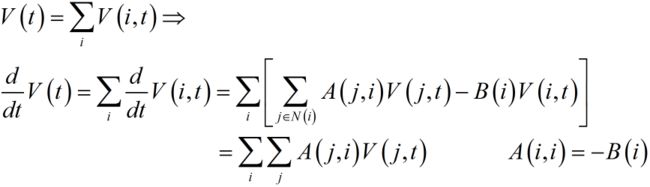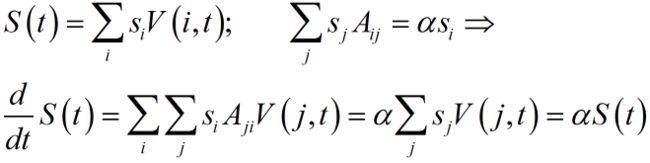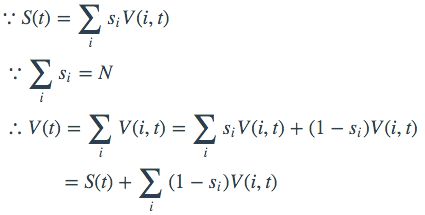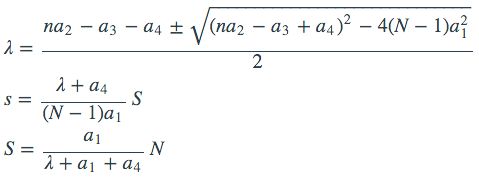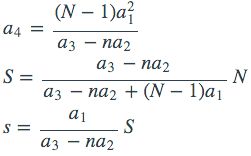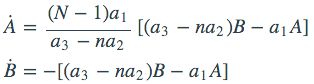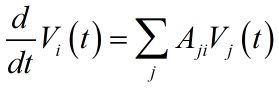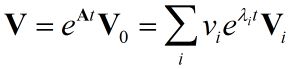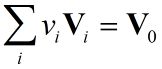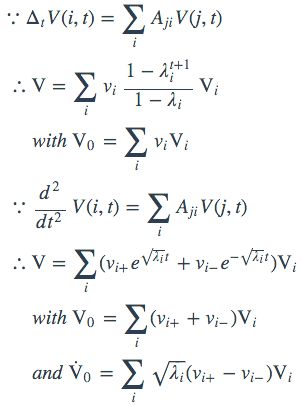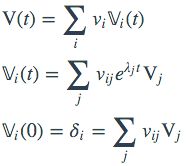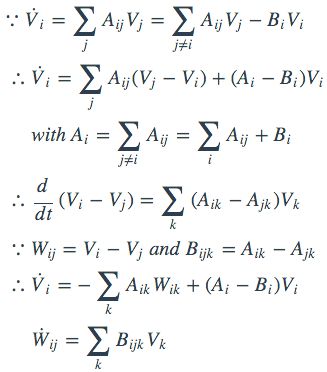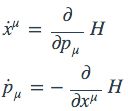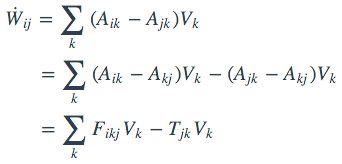嗯,这篇真的只是一篇笔记哟~~~或者更可以说就是一段草稿…………
问题的由来,是这样的:假定我们有一个由N个节点构成的网络,每个节点p(i)上都有一个值V(i)(值域为F),然后任意两个节点P(i)与P(j)之间存在一个“作用”,从而使得网络上任意节点上值的改变满足如下关系:
这里A和B自然就是上述“作用”的系数了,但它们作用在值V上也并不是简单的乘法,因为V属于值域F,所以A和B可以是F上的任意算子。求和范围N(i,t)则是t时刻节点P(i)的“邻点集”,我们当然可以将其拓展到全空间,只要那些原本不在该邻点集内的点现在的作用恒为0即可,从而可以写为:
再进一步,我们也并不仅局限在对时间的微分这一种动力学模型上,也完全可以是差分:
这里有趣的地方是:我们并不要求每个节点上的更新速度是相同的,于是,完全可以某些节点每秒更新一次,而某些节点每分钟更新一次,这样就会很有意思,当然,是否有意义有实际应用价值,这个再议。
甚至于,也可以是对时间的二阶导或者二阶差分,这取决于我们所要解决的问题在动力学方面究竟具有什么样的特性。
在下面,我们主要考虑关于时间的一阶微分的情况。
上面只是在介绍这个问题的大背景,而个人所感兴趣的是:这样的系统中是否存在某些可以全局性描述整个系统的量?
我们先从一个简单的角度入手:假定值域就是我们熟悉的实数域,而作用就是通常的乘法,且作用大小固定,节点的连接形式固定,考虑的也是时间上连续的系统,于是整个系统的动力学方程就可以写为:
接下来,我们考虑整个网络上的V的总量V(t)的变化方程:
这里,我们就可以发现一件很有趣的事:如果作用矩阵A非退化,那么自然就可以构造如下不变量:
这里将系数集si可以看作给出了每个节点的权重,本质上则是作用矩阵Aij的特征向量,相应的α就是特征值,而S(t)则是整个网络的加权总V值。由于最多的时候,一个N阶矩阵可以有N个特征值,所以这样的加权方式往往不止一种。
当权重固定下来后,加权总V值的变化就是一个很简单的方程:
我们可以考虑一个极特殊的情况,即特征值为0的情况,那么此时加权总V就是一个常量。
而在这种情况下,一个有趣的问题就是真正的总V即V(t)会是什么样的呢?
我们可以选择一个“归一化”权重,满足所有权重之和为节点总数N,从而就有:
由此我们可以看出,总V可以看做加权V的基础上加上一些“扰动”,而权重为0的节点所给出的扰动贡献为0,权重大于1的节点则给出负贡献,权重小于1的节点给出的则是正贡献的扰动。
作为例子,我们可以考虑一个极端的情况:所有N个节点中,有N-1个节点具有相同的权重s,而只有一个节点具有不同的权重S,从而按照归一化条件,我们有S=N-(N-1)s。我们可以进一步假定这特殊的点是P(1),从而在这个情况下,总V就可以表示为:
可见,如果P(1)节点上的权重是一个大于1的值,即这里s<1,那么总V会随着该节点上的V值的增加而减少;反之,如果P(1)节点上的权重小于1,则总V将随着该点上的V值的增加而增加。
接下来,有一个很自然的问题,就是在这样的系统上,V(1,t)到底是会变大还是变小呢?
在这里所选的权重模型下,我们可以进一步“猜测”整个网络的结构可以如此来构造:
除了1号点的所有点,都有固定的n个不包括1号点的邻点,而1号点是所有点的邻点。然后所有相邻关系的点之间的作用是相等的,即Aij=Aji。这样的结构我们自然就得到特征值与特征向量:
其中λ为特征值,S为1号点的权重,s为其余点的权重,a1是1号点与别的点之间的作用系数,a2是1号点之外的点之间的作用系数,a3是1号点之外的点的B(i)系数,即-Aii,相应的a4就是-A11了。n是1号点之外的邻点数,N是总节点数。
现在的特征向量
这个约定仅仅是为了构造出一个恒定不变的加权总V,方便讨论。
现在,总V的动力学方程为:
如果我们假定出了1号节点外别的节点的V值始终相等,那么可以使用A(t)表示V(1,t),B(t)表示V(>1,t),从而有:
这个方程有解:
其中S0是系统加权总V,是一个恒定值;A0是1号点的初始V值。
不难发现,在上述设定下,系统最后将趋于一个稳定态,而在这个状态下,特殊的1号点与别的点上的V值比,也恰好就是整个网络节点权重之间的比。
这个结果非常具有启发性。
因此,一个我们非常感兴趣的问题自然就出现了:就最普遍的意义来说,这个网络在如此的动力学方程下,究竟会给出什么样的普适结果呢?
让我们回到最开始的方程:
它自然可以写成一种更加自然的形式:
这里V是N阶列向量,A是N阶方阵,从而这是一个很常见的矩阵的常微分方程,其解为:
其中V0是初始值,Vi是第i个特征矢量,λi是对应的特征值,vi则是相应的自由系数。
第一个表达是形式解,而第二个是用特征值与特征向量构造出的一般解,其要满足初始化条件:
从这里不难看出,所有那些负特征值给出的衰减项,而最大特征值对应的特征矢量就决定了网络演化的最终结局。
我们当然可以不仅局限在对时间的一阶微分方程这一个形式上,比如对于差分方程或者二阶微分方程,我们也一样有类似的结果:
因此,现在原则上此类方程都可以通过这个方法求出。
非但如此,即便是作用矩阵A不是常值的情况,原则上也依然可以通过类似的方法求出。
因此,现在对于一阶或者二阶的微分或者差分问题,我们都有了比较统一的解决方案,至少形式上如此。这类扩散问题(对应一阶动力学方程)或者波动问题(对应二阶动力学方程)都由整个网络的结构即作用矩阵A给出,而且结果显然是线性的。
由线性这一特点,我们可以进一步做一个分解(以一阶为例):
其中中空的粗体V表示新的一组随时间而改变的基,而δi则是第i节点V值为1,别的所有节点V值为0的笛卡尔形单位正交基。
这么一来,当我们有了这组基后,只要知道初始状态就可以通过这组基的线性叠加得到整个网络此后的发展。
在这个基础上,我们还可以看到一些别的有趣的东西,比如下面这种“对偶性”(对于一阶动力学系统)(下面的Aij和上面的Aij的定义正好相反,是从j指向i的):
是不是觉得特眼熟?和哈密顿方程在某种程度上是很相似的:
当然,这仅仅是YY出来的相似而已。
回到属性V在ij这两个节点上的差W与V的动力学关系上来,我们发现如果Ai=Bi对任意时刻的任意节点都成立的话,那么这种对偶性将更加显然。而这样的节点很显然地具有特征值0,从而是一个总V守恒的网络,这是一个很不错的性质。这样的网络可以被称为守恒网络。
让我们对上述方程做一个变形:
这里Fikj可以看做从j经过k流向i的作用,而Tjk则表示了k节点到j节点之间的流出流入差。对于T恒为零的网络,可以称之为对称网络。
显然,如果网络是守恒的或者对称的,那么这样的网络当然是具有很好的性质的,但现实中我们所遇到的网络很多未必有这样的好性质。
除了网络上的作用与流,网络还有一些别的与结构相关的性质。
比如说,网络上的一条“路径”,便是一连串的节点,其中相邻的两个节点相连——在非对称的情况下,则是存在从前一个节点到后一个节点的有向箭头。
有了路径,当然就可以来计算路径的“长度”:将路径记为p,则p是一个节点指标的有序数组,从而p的长度就是这个有序数组的元素数。
进一步,从A到B的所有路径中最短的那条路径的长度,就是从A到B的距离——这里需要注意,在有向图中,从A到B的距离并不等于从B到A的距离。
同时,如果不存在一条从A到B的路径也不存在一条从B到A的路径,那便是说A与B是分离的;如果存在从A到B的路径而不存在从B到A的路径,那A与B便是半分离的;否则,则称A与B相连。
如果一个点集中任意两点都相连,则该点集为连通的,否则则成为断裂的。如果在全集中,一个连通点集中存在至少一个点,与该点集外的任一点都不相连,则该点集为孤立的。
进一步,我们可以定义连通点集中任意两点之间距离的最大值,为该点集的直径。
于是,一个很自然的问题就出现了:给定一个点集构成的上述网络,是否存在一个简单的方法来判断该网络是否连通?
我们可以从最简单的一类网络模型开始考虑这个问题:
假定网络中总共有N个节点,每个节点都与自身以外的n个不同点相邻,那么在这样的模型中,n与N满足什么样的关系时,网络几乎可以肯定会断裂?
这便是下一篇文章要讨论的一个主要问题。
本文遵守创作共享CC BY-NC-SA 4.0协议
通过本协议,您可以分享并修改本文内容,只要你遵守以下授权条款规定:姓名标示 、非商业性、相同方式分享。
具体内容请查阅上述协议声明。
本文禁止一切纸媒,即印刷于纸张之上的一切组织,包括但不限于转载、摘编的任何应用和衍生。网络平台如需转载必须与本人联系确认。
如果喜欢,想要下载App的话,轻戳这里~~
私人推荐订阅专题:《有意思的文章》、《严肃码匠圈》