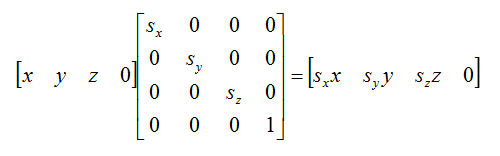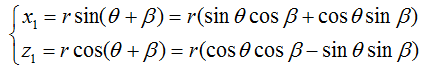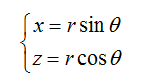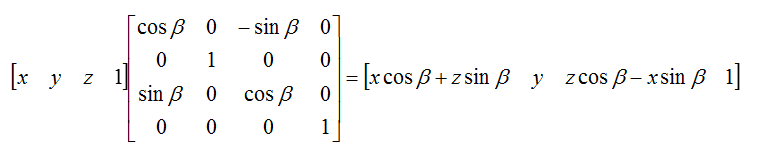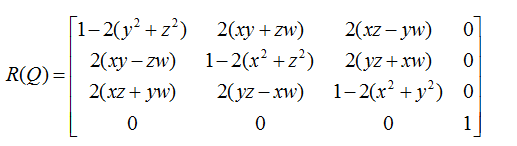理解了绘制管线,我们发现其中充满对矩阵和向量等数学工具的运用,在实现流水线之前,我们需要实现一套自己的C++数学库。
为了方便管理,先定义一些常用的数据类型
using _DOUBLE = double;
using _FLOAT = float;
using _LONG = long;
using _INT32 = int;
using _UINT32 = unsigned int;
using _CHAR = char;
using _BYTE = char;
using _PSTR = char*;
using _PBYTE = char*;
using _PVOID = void*;
以及一些常用数值的宏
#define PI 3.1415926f
#define HALF_PI 1.5707963f
#define COLOR_MIN 0.0f
#define COLOR_MAX 1.0f
#define PTR_SIZE sizeof(_PVOID)
#define BYTE_SIZE sizeof(_BYTE)
向量(Vector)
我们需要用到Vector2f, Vector2i, Vector3f, Vector4f,其中2维和3维向量用来表示屏幕坐标和空间坐标,4维向量用来表示其次坐标。
其次坐标是在三维向量的基础之上加入了新的分量w,当向量表示一个点的时候w=1,当向量表示方向的时候w=0。
其次坐标产生的原因是3*3的矩阵是不能表示平移变化的,为了表示平移变化需要4*4的矩阵,所以在进行顶点变化的时候需要使用给向量加一个新的分量。
其次坐标在进行向量计算的时候我们只需要考虑它的x y z分量即可,而第四个分量w这里不用进行特殊处理。
Vector4f的声明如下
class Vector4f
{
public:
_FLOAT _x, _y, _z, _w;
public:
Vector4f(){}
Vector4f(const Vector3f& other);
Vector4f(_FLOAT x, _FLOAT y, _FLOAT z, _FLOAT w);
Vector4f(const Vector4f& other);
Vector4f& operator = (const Vector4f& other);
public:
_FLOAT Length() const;
Vector4f Normalize();
_FLOAT Dot(const Vector4f& v) const;
Vector4f Cross(const Vector4f& v) const;
Vector4f operator + (const Vector4f& v) const;
Vector4f operator - (const Vector4f& v) const;
Vector4f operator * (const Vector4f& v) const;
Vector4f operator * (_FLOAT scale) const;
Vector4f operator * (const Matrix4f& m) const;
Vector4f operator - () const;
bool operator == (const Vector4f& other) const;
};
- 构造函数、赋值构造函数、复制构造函数
Vector4f::Vector4f(const Vector3f& other) : _x(other._x), _y(other._y), _z(other._z), _w(1.0f)
{
}
Vector4f::Vector4f(_FLOAT x, _FLOAT y, _FLOAT z, _FLOAT w) : _x(x), _y(y), _z(z), _w(w)
{
}
Vector4f::Vector4f(const Vector4f& other) : _x(other._x), _y(other._y), _z(other._z), _w(other._w)
{
}
Vector4f& Vector4f::operator = (const Vector4f& other)
{
if (&other != this)
{
_x = other._x;
_y = other._y;
_z = other._z;
_w = other._w;
}
return *this;
}
- 点积
点积的代数定义:a =(m,n,o),b =(p,q,r),ab =mp+nq+or
点积的几何定义:a·b =|a||b|cosθ
其中|a|,|b|为a,b的模长。
_FLOAT Vector4f::Dot(const Vector4f& v) const
{
return _x * v._x + _y * v._y + _z * v._z;
}
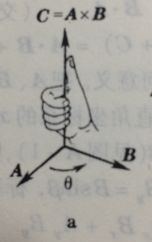
- 叉积
与点积不同,叉积的结果是一个向量,叉积的方向根据坐标系的不同需要用不同的手进行判断,左手系用左手,右手系用右手。
)
叉积的代数定义:a =(ax,ay,az),b =(bx,by,bz),a×b =(ay·bz-az·by, az·bx-ax·bz,ax·by-ay·bx)
叉积的几何定义:|a×b| =|a||b|sinθ
Vector4f Vector4f::Cross(const Vector4f& v) const
{
_FLOAT x = _y * v._z - _z * v._y;
_FLOAT y = _z * v._x - _x * v._z;
_FLOAT z = _x * v._y - _y * v._x;
return Vector4f(x, y, z, 1.0f);
}
- 求模
_FLOAT Vector4f::Length() const
{
_FLOAT square = _x * _x + _y * _y + _z * _z;
return sqrtf(square);
}
- 单位化
Vector4f Vector4f::Normalize()
{
_FLOAT length = Length();
if (length != 0)
{
_FLOAT inverse = 1.0f / length;
_x *= inverse;
_y *= inverse;
_z *= inverse;
}
return *this;
}
- 加减乘除
加法和减法简单将每一个分量相加减就好了。
Vector4f Vector4f::operator + (const Vector4f& v) const
{
_FLOAT x = _x + v._x;
_FLOAT y = _y + v._y;
_FLOAT z = _z + v._z;
return Vector4f(x, y, z, 1.0f);
}
Vector4f Vector4f::operator - (const Vector4f& v) const
{
_FLOAT x = _x - v._x;
_FLOAT y = _y - v._y;
_FLOAT z = _z - v._z;
return Vector4f(x, y, z, 1.0f);
}
乘法分为两种情况
1.一种是一个向量乘以一个常数,这种情况只需要让向量的每一个分量乘以这个常数即可。
Vector4f Vector4f::operator * (_FLOAT scale) const
{
_FLOAT x = _x * scale;
_FLOAT y = _y * scale;
_FLOAT z = _z * scale;
return Vector4f(x, y, z, 1.0f);
}
2.另一种是两个向量相乘(这个情况你可能在数学书上找不到),对于这种情况只需要将向量对应分量相乘就可以了
Vector4f Vector4f::operator * (const Vector4f& v) const
{
_FLOAT x = _x * v._x;
_FLOAT y = _y * v._y;
_FLOAT z = _z * v._z;
return Vector4f(x, y, z, 1.0f);
}
- 求反
Vector4f Vector4f::operator - () const
{
return Vector4f(-_x, -_y, -_z, 1.0f);
}
- 判断两个向量是否相等
bool Vector4f::operator == (const Vector4f& other) const
{
return Equal(_x, other._x) && Equal(_y, other._y) && Equal(_z, other._z);
}
矩阵(Matrix)
在这个光栅器中我们使用4*4的矩阵来统一的表示表示平移、选择和缩放变换。
Matrix4f的声明如下
class Matrix4f
{
public:
_FLOAT _data[4][4];
public:
Matrix4f(){};
Matrix4f(
_FLOAT a11, _FLOAT a12, _FLOAT a13, _FLOAT a14,
_FLOAT a21, _FLOAT a22, _FLOAT a23, _FLOAT a24,
_FLOAT a31, _FLOAT a32, _FLOAT a33, _FLOAT a34,
_FLOAT a41, _FLOAT a42, _FLOAT a43, _FLOAT a44
);
Matrix4f(const Matrix4f& other);
_FLOAT& operator () (_INT32 i, _INT32 j);
Matrix4f& operator = (const Matrix4f& other);
public:
static Matrix4f Identity();
static Matrix4f Zero();
void SetIdentity();
void SetZero();
void SetTranslation(_FLOAT x, _FLOAT y, _FLOAT z);
void SetScale(_FLOAT x, _FLOAT y, _FLOAT z);
void SetRotation(Vector4f& axis, _FLOAT theta);
Matrix4f operator + (const Matrix4f& m) const;
Matrix4f operator - (const Matrix4f& m) const;
Matrix4f operator * (const Matrix4f& m) const;
Matrix4f operator * (_FLOAT scale) const;
Matrix4f operator - () const;
bool operator == (const Matrix4f& other) const;
};
- 构造函数、赋值构造函数、复制构造函数
Matrix4f::Matrix4f(
_FLOAT a11, _FLOAT a12, _FLOAT a13, _FLOAT a14,
_FLOAT a21, _FLOAT a22, _FLOAT a23, _FLOAT a24,
_FLOAT a31, _FLOAT a32, _FLOAT a33, _FLOAT a34,
_FLOAT a41, _FLOAT a42, _FLOAT a43, _FLOAT a44
)
{
_data[0][0] = a11; _data[0][1] = a12; _data[0][2] = a13; _data[0][3] = a14;
_data[1][0] = a21; _data[1][1] = a22; _data[1][2] = a23; _data[1][3] = a24;
_data[2][0] = a31; _data[2][1] = a32; _data[2][2] = a33; _data[2][3] = a34;
_data[3][0] = a41; _data[3][1] = a42; _data[3][2] = a43; _data[3][3] = a44;
}
Matrix4f::Matrix4f(const Matrix4f& other)
{
for (auto i = 0; i < 4; i++)
{
for (auto j = 0; j < 4; j++)
{
_data[i][j] = other._data[i][j];
}
}
}
Matrix4f& Matrix4f::operator = (const Matrix4f& other)
{
if (&other != this)
{
for (auto i = 0; i < 4; i++)
{
for (auto j = 0; j < 4; j++)
{
_data[i][j] = other._data[i][j];
}
}
}
return *this;
}
- 重载()操作符方便取值
_FLOAT& Matrix4f::operator () (_INT32 i, _INT32 j)
{
return _data[i][j];
}
- 单位矩阵
对角线上的元素全为1,其他位置全为0的矩阵称为单位矩阵
任何矩阵和单位矩阵相乘的结果都还是原来的矩阵,即 : M·I=I·M=M
Matrix4f Matrix4f::Identity()
{
Matrix4f ans;
ans._data[0][0] = 1.0f; ans._data[0][1] = 0.0f; ans._data[0][2] = 0.0f; ans._data[0][3] = 0.0f;
ans._data[1][0] = 0.0f; ans._data[1][1] = 1.0f; ans._data[1][2] = 0.0f; ans._data[1][3] = 0.0f;
ans._data[2][0] = 0.0f; ans._data[2][1] = 0.0f; ans._data[2][2] = 1.0f; ans._data[2][3] = 0.0f;
ans._data[3][0] = 0.0f; ans._data[3][1] = 0.0f; ans._data[3][2] = 0.0f; ans._data[3][3] = 1.0f;
return ans;
}
void Matrix4f::SetIdentity()
{
_data[0][0] = 1.0f; _data[0][1] = 0.0f; _data[0][2] = 0.0f; _data[0][3] = 0.0f;
_data[1][0] = 0.0f; _data[1][1] = 1.0f; _data[1][2] = 0.0f; _data[1][3] = 0.0f;
_data[2][0] = 0.0f; _data[2][1] = 0.0f; _data[2][2] = 1.0f; _data[2][3] = 0.0f;
_data[3][0] = 0.0f; _data[3][1] = 0.0f; _data[3][2] = 0.0f; _data[3][3] = 1.0f;
}
- 零矩阵
顾名思义,零矩阵就是所有位置全为0的矩阵
任何矩阵和零矩阵相乘的结果都是零矩阵,即:M·0=0·M=0
Matrix4f Matrix4f::Zero()
{
Matrix4f ans;
for (auto i = 0; i < 4; i++)
{
for (auto j = 0; j < 4; j++)
{
ans._data[i][j] = 0.0f;
}
}
return ans;
}
void Matrix4f::SetZero()
{
for (auto i = 0; i < 4; i++)
{
for (auto j = 0; j < 4; j++)
{
_data[i][j] = 0.0f;
}
}
}
- 矩阵的加法和减法
矩阵的加法和减法比较简单,只需要把对应每个位置上的元素相加减,得到一个新的矩阵
Matrix4f Matrix4f::operator + (const Matrix4f& m) const
{
Matrix4f ans;
for (auto i = 0; i < 4; i++)
{
for (auto j = 0; j < 4; j++)
{
ans._data[i][j] = _data[i][j] + m._data[i][j];
}
}
return ans;
}
Matrix4f Matrix4f::operator - (const Matrix4f& m) const
{
Matrix4f ans;
for (auto i = 0; i < 4; i++)
{
for (auto j = 0; j < 4; j++)
{
ans._data[i][j] = _data[i][j] - m._data[i][j];
}
}
return ans;
}
- 矩阵的乘法
矩阵的乘法分为三种情况
1.当矩阵与一个数相乘的时候,只需要把矩阵的每一个元素与这个数相乘,得到一个新的矩阵
Matrix4f Matrix4f::operator * (_FLOAT scale) const
{
Matrix4f ans;
for (auto i = 0; i < 4; i++)
{
for (auto j = 0; j < 4; j++)
{
ans._data[i][j] = scale * _data[i][j];
}
}
return ans;
}
2.当矩阵与一个向量相乘的时候,要注意左乘和右乘的结果是不同的
我们这里使用向量左乘矩阵
Vector4f Vector4f::operator * (const Matrix4f& m) const
{
return Vector4f(
_x * m._data[0][0] + _y * m._data[1][0] + _z * m._data[2][0] + _w * m._data[3][0],
_x * m._data[0][1] + _y * m._data[1][1] + _z * m._data[2][1] + _w * m._data[3][1],
_x * m._data[0][2] + _y * m._data[1][2] + _z * m._data[2][2] + _w * m._data[3][2],
_x * m._data[0][3] + _y * m._data[1][3] + _z * m._data[2][3] + _w * m._data[3][3]
);
}
3.当两个矩阵相乘的时候,计算方式如下
Matrix4f Matrix4f::operator * (const Matrix4f& m) const
{
Matrix4f ans;
for (auto i = 0; i < 4; i++)
{
for (auto j = 0; j < 4; j++)
{
ans._data[i][j] =
_data[i][0] * m._data[0][j] +
_data[i][1] * m._data[1][j] +
_data[i][2] * m._data[2][j] +
_data[i][3] * m._data[3][j];
}
}
return ans;
}
- 求反
Matrix4f Matrix4f::operator - () const
{
Matrix4f ans;
for (auto i = 0; i < 4; i++)
{
for (auto j = 0; j < 4; j++)
{
ans._data[i][j] = -_data[i][j];
}
}
return ans;
}
- 判断两个矩阵是否相等
两个矩阵相等(不是等价)的充要条件是对应位置的元素相等
bool Matrix4f::operator == (const Matrix4f& other) const
{
bool equal = true;
for (auto i = 0; i < 4; i++)
{
for (auto j = 0; j < 4; j++)
{
if (Equal(_data[i][j], other._data[i][j]) == false)
{
return false;
}
}
}
return true;
}
- 平移变换矩阵
我们前面说过,在对点进行矩阵变换的时候使用的是其次坐标,而对于一个点来说它的第四个分量w值为1,这里就可以知道这是为什么了。
可以看到只有当w=1的时候偏移量才会被正确的作用到点上
而对一个方向进行平移变换是不会产生任何影响的
void Matrix4f::SetTranslation(_FLOAT x, _FLOAT y, _FLOAT z)
{
SetIdentity();
_data[3][0] = x;
_data[3][1] = y;
_data[3][2] = z;
}
- 缩放变换矩阵
我们可以使用下列矩阵对点或者方向进行缩放变换
void Matrix4f::SetScale(_FLOAT x, _FLOAT y, _FLOAT z)
{
SetIdentity();
_data[0][0] = x;
_data[1][1] = y;
_data[2][2] = z;
}
- 旋转变换矩阵
旋转矩阵是三种常见变换中最复杂的一种,一般来说旋转变换需要指定一个旋转轴,这个旋转轴可以是空间中的任意一个方向,然后再指定一个旋转角度,这样就能定义任意一个旋转变换了。
首先讨论简单的情况,即绕坐标轴旋转,现有下面的右手坐标系
当我们绕y轴旋转β弧度的时候,旋转的过程中y坐标的值不会发生改变,只有x和y发生变化,问题就变成了下面的情况
旋转的过程中顶点到原点的距离不会发生变化,所以有
已知点(x,y)的坐标满足下式
把①代入到②中有
然后我们把③写成矩阵的形式,得到
由于整个旋转的过程中y是不变的,最后就可以得到
绕x和z轴旋转的情况同理可以推到出来。
但是对于绕任意轴旋转的情况,上面的方法就行不通了,这里我们引入一个新的概念叫做四元数,四元数其实还是比较复杂的,有兴趣的同学可以参考四元数的维基百科。
四元数的定义如下,如果绕轴n旋转θ弧度,则四元数Q为
四元数的模
四元数的共轭,四元数和它的共轭代表相反的角位移,因为旋转轴的方向是相反的
四元数的逆(是不是觉得和矩阵的逆特别像?)
使用四元数对空间中点进行旋转
这里我们想要统一用矩阵来表示所有的变换,可以使用下面的公式
void Matrix4f::SetRotation(Vector4f& axis, _FLOAT theta)
{
_FLOAT halfTheta = theta * 0.5f;
_FLOAT sinHalfTheta = sinf(halfTheta);
_FLOAT cosHalfTheta = cosf(halfTheta);
Vector4f axisNormal = axis.Normalize();
_FLOAT x = axisNormal._x * sinHalfTheta;
_FLOAT y = axisNormal._y * sinHalfTheta;
_FLOAT z = axisNormal._z * sinHalfTheta;
_FLOAT w = cosHalfTheta;
_FLOAT x2 = x * x; _FLOAT y2 = y * y; _FLOAT z2 = z * z;
_FLOAT xy = x * y; _FLOAT xz = x * z; _FLOAT yz = y * z;
_FLOAT xw = x * w; _FLOAT yw = y * w; _FLOAT zw = z * w;
_data[0][0] = 1 - 2 * (y2 + z2);
_data[1][0] = 2 * (xy - zw);
_data[2][0] = 2 * (xz + yw);
_data[3][0] = 0.0f;
_data[0][1] = 2 * (xy + zw);
_data[1][1] = 1 - 2 * (x2 + z2);
_data[2][1] = 2 * (yz - xw);
_data[3][1] = 0.0f;
_data[0][2] = 2 * (xz - yw);
_data[1][2] = 2 * (yz + xw);
_data[2][2] = 1 - 2 * (x2 + y2);
_data[3][2] = 0.0f;
_data[0][3] = 0.0f;
_data[1][3] = 0.0f;
_data[2][3] = 0.0f;
_data[3][3] = 1.0f;
}
其他的一些函数
交换两个变量
template
void Swap(T& x, T& y)
{
T tmp = x;
x = y;
y = tmp;
}
求int类型变量的绝对值
_INT32 Abs(_INT32 x)
{
return x > 0 ? x : -x;
}
求float类型变量的绝对值
_FLOAT Abs(_FLOAT x)
{
return x > 0 ? x : -x;
}
判断两个浮点型的变量是否相等,这里很重要,因为在整个光栅器中涉及到了大量的对浮点数的运算,而浮点数的表示是不准的(诸如1.0f / 3.0f * 3.0f 是不等于1.0f的),所以判断两个浮点数是否相等只需要看它们之间的差是否足够的小即可。
bool Equal(_FLOAT x, _FLOAT y, _FLOAT epsilon)
{
return abs(x - y) < epsilon ? true : false;
}
浮点数的线性插值
_FLOAT Interpolate(_FLOAT x, _FLOAT y, _FLOAT t)
{
return x + (y - x) * t;
}
4维向量的线性插值
Vector4f Interpolate(Vector4f& v1, Vector4f& v2, _FLOAT t)
{
return Vector4f(Interpolate(v1._x, v2._x, t), Interpolate(v1._y, v2._y, t), Interpolate(v1._z, v2._z, t), 1.0f);
}
3维向量的线性插值
Vector3f Interpolate(Vector3f& v1, Vector3f& v2, _FLOAT t)
{
return Vector3f(Interpolate(v1._x, v2._x, t), Interpolate(v1._y, v2._y, t), Interpolate(v1._z, v2._z, t));
}
将变量限制在闭区间[min,max]中
_FLOAT Range(_FLOAT value, _FLOAT min, _FLOAT max)
{
if (value < min)
{
return min;
}
if (value > max)
{
return max;
}
return value;
}