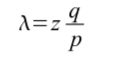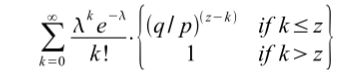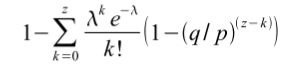版权声明:本文版权归属麻烦的名字,如需转载,请与作者联系。同时,本文授权BH好文好报群摘编、转载以及相关转授权推文行为。
简介:本文对比特币论文原稿进行了拆分,分为一、二、三、四四个部分,并将以四篇文章先后对这四部分进行翻译。翻译原文的目的,是为了加深自己对比特币以及区块链原理的认识,同时,也为广大想要了解比特币原文的读者们提供一个渠道。希望本文的翻译对您有帮助。文末有原文链接,想要了解的朋友可以自行查阅。
2018年7月13日
比特币论文原稿之翻译(四)
10.隐私
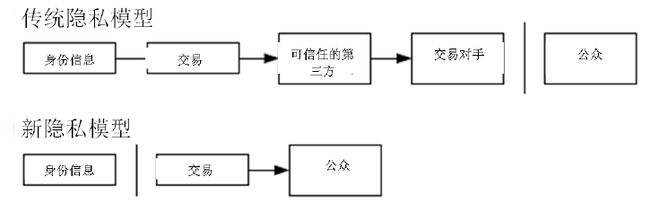
传统的银行业务模型通过限制访问合作方机构或者第三方机构的信息来保护个人隐私。但是如果将交易信息向全网进行公开宣布,就意味着这样的方法就失效了。但是隐私还是可以得到保护:通过保持公钥的匿名性。通过公钥可以看到某人向另外一个人发送了一定数量的金额,但是任何人都看不到交易的详细信息。这和股票交易所发布的信息是类似的,股票的交易的时间和交易数量是公开的,但是交易双方的身份信息却不是公开的。
作为一层额外的防火墙,使用者可以为每次交易生成一个新的地址,防止这些交易被追溯到一个共同的拥有者。但是由于并行输入的存在,在一定程度上被追溯是无法避免的。因为并行输入揭穿了这些货币是属于同一个拥有者。这种情况的风险在于,一旦某个拥有者的公钥被揭露了,那么就可以追溯到此人其他的多笔交易信息。
11.计算
我们考虑到了这么一个场景:一个攻击者试图创建一条比诚实节点更快的,并且可以替换的链条。但是整个系统也并非就此完全受制于攻击者的独断意志,例如凭空创造价值,或者掠夺原本不属于攻击者的货币。节点不会把一个无效的交易当成支付,而且节点从来都不会接受一个包含无效交易的区块。一个攻击者能做的,仅仅是改变他自己的交易信息,并且要回自己已经支付的钱。
诚实链和攻击链之间的比赛可以用二项随机漫步来描述。成功事件是诚实链条被一个区块扩展,使得其领先性+1;失败事件是攻击者的链条被一个区块扩展,使得差距-1。
攻击者弥补某一既定差距的概率,可以看作是赌徒破产问题。假设一个赌徒拥有无限的透支信用,然后开始进行潜在次数为无限的赌博,并试图填补上自己的亏空。我们可以计算出他填补上亏空的概率,或者一个攻击者赶上诚实节点的概率,计算过程如下所示:
假设p>q,那么攻击成功的概率就随着区块的增长而呈指数化下降。如果攻击者不能幸运且快速地获得成功,那么随着时间的流逝,他获得成功的概率会越来越渺茫。
我们现在考虑的是接受者需要等待多长时间才能充分地确认一笔交易没有被发送者改动过。我们假设发送者是一名攻击者,他想让接收者在一段时间内相信自己已经收到款,然后,在这段时间过后再将钱转回到自己的账户中。当这种情况发生的时候,接受者之后意识到,但是为时已晚。
接收者生成了一对密钥,并且在签名之前把其中的公钥传给了发送者。这将可以防止此种情况:发送者预先准备好一个区块链,然后持续地对它进行运算,直到他的运气好到让他超越诚实的链条,然后才会立即执行交易。一旦交易发生之后,攻击者就开始秘密地准备一条包含了该交易替代版本的链条。
接收者会一直等待,直到这笔交易被纳入一个区块中,随后z个区块会连接到这个区块后面。但是,他仍然不能确定攻击者在这个过程中生成了多少个区块,假设诚实的区块在平均期望时间里生成一个区块,那么攻击者潜在的进展就会呈泊松分布,分布的期望值为:
为了得到攻击者追赶上的概率,我们将攻击者取得的进展区块数量的泊松分布概率密度,乘以在该数量下攻击者仍然能够追赶上的概率。
转换为如下公式,避免对无线数列求和:
转换成C语言代码:
#includedouble AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
运行之后,我们得到了一些结果,从结果中可以看出来,随着z的增加,概率呈指数减少。
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
求解令p值小于0.1%的z值:
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
12.总结
我们提出了一个不需要依赖第三方机构的电子支付系统。我们首先讨论了普通的电子现金系统的数字签名原理。虽然这为所有权的控制提供了强大的支撑,但是由于缺乏解决双重支付问题的有效途径,使得这个原理显得不是那么完善。为了解决这个问题,我们使用了一种点对点的网络,它利用工作量证明机制去记录交易的历史信息,并将这些信息公布到网络中。如果诚实的节点控制了绝大多数的CPU计算能力,那么黑客企图改变这些交易信息在计算上是不可能实现的。该网络的稳健之处在于其非结构化的简洁性。节点的工作大部分时间是独立的,很少需要协同工作。节点不需要进行身份验证,因为这些信息不能追溯到参与者的地点,所以只需要尽最大努力传播就行。节点可以选择离开网络或者重新加入网络,它们通过接收工作量证明的链条作为它们离开网络的证据。各个节点通过CPU的计算能力进行投票,它们通过在有效的区块上工作并扩展区块来表达它们接收了这个区块,通过拒绝在区块上工作来表达它们拒绝无效的区块。任何需要的规则和激励措施将会随着共识机制的增强而增强。
比特币论文原稿:https://bitcoin.org/bitcoin.pdf
早赞声明:为方便早赞、避免乱赞,“BH好文好报群”为点赞者、写作者牵线搭桥,实行“先审后赞、定时发表”的规则,也让作品脱颖而出、速登热门!加群微信:we01230123(天平)