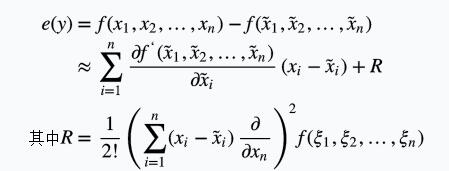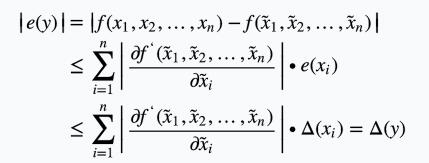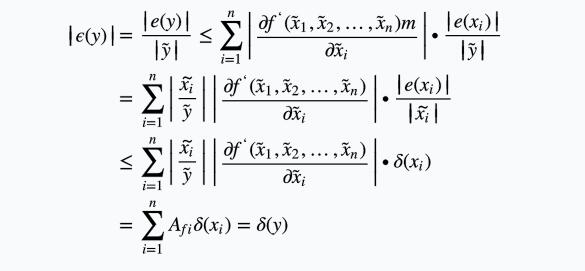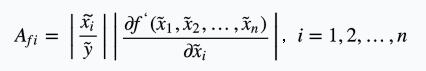数值分析读书笔记（1）导论

数值分析读书笔记（1）导论

1.数学问题与数值计算问题

一般来说，解决实际问题的第一步是将实际问题转换为数学问题，接着建立数学模型来解决这个数学问题，而理论解或者解析解通常难以求得，于是数值计算的方法应运而生

首先我们要将一个数学问题转化成数值问题

数值问题是指输入数据与输出数据之间函数关系的一个确定而无歧义的描述

按照建立数值问题的基本形式，数学问题可以分为两大类

• 包含非有理函数或未知函数
• 主要是代数问题

这一本书面向数值计算的三大类计算任务

• 求值（计算机实现计算过程中遇到的问题）
• 方程求解
  • 数值方程
    • 代数方程
    • 超越方程
    • 差分方程（组）
  • 函数方程
• 函数逼近

数学与科学，工程中的大量问题，最后归结为数值线性代数问题，这一大类问题通常和矩阵有关，故又称为矩阵计算
数值线性代数包括

• 规范线性方程组问题
• 非规范线性方程组问题
• 矩阵的特征值问题(包括广义特征值)
• 矩阵的奇异值问题

2.数值计算的基本数学思想与方法

构造数值计算方法的基本途径是近似

由于是导论，故不深入探讨，这里列出几种思想

• 等价变换思想（相似变换处理矩阵）
• 逐次逼近思想（不动点迭代）
• 逐步逼近思想
• 以直代曲思想
• 转换问题类型思想
• 外推思想（Richardson 外推法）

数值计算的几种方法

• 直接法（不考虑舍入误差的情况下，有限步得到精确解）
• 间接法（迭代过程，让近似解逼近精确解）

数值方法的评价标准

• 计算效果（精度或者误差）
• 计算效率（算法复杂度或者收敛率）

3.计算误差的基本概念以及误差分析

数值计算的误差是指数学模型的真解和由数值方法得到的近似解之间的偏差

误差按来源可以这样分类

• 模型误差
• 观测误差
• 截断误差
• 舍入误差

这里引入绝对误差，相对误差和有效数字的概念

首先是绝对误差 =x-\tilde {x}$$) , 其中为x的近似值,我们可以得到绝对误差界
 \end{vmatrix} =\begin{vmatrix} x-\tilde x \end{vmatrix} \le \Delta (x) =\Delta $)

然而绝对误差并不能很好的表现数的近似程度，引出相对误差
 = \frac{e(x)}{x} =\frac{x-\tilde x}{x} $$)
自然也有相对误差界*
![](http://www.forkosh.com/mathtex.cgi?
$$\begin{vmatrix} \epsilon ^ * \end{vmatrix} = \begin{vmatrix} \epsilon ^ * (x) \end{vmatrix} = \begin{vmatrix} \frac{e(x)}{x} \end{vmatrix}=\begin{vmatrix}\frac{x-\tilde x}{x}\end{vmatrix} \le \delta ^*(x)=\delta*$$)
注意到分母为x,而实际当中我们经常用来代替分母，即![](http://www.forkosh.com/mathtex.cgi?
$$\begin{vmatrix}\epsilon\end{vmatrix}= \begin{vmatrix} \epsilon (x) \end{vmatrix}= \begin{vmatrix} \frac{e(x)}{\tilde x} \end{vmatrix}=\begin{vmatrix} \frac{x-\tilde x}{\tilde x} \end{vmatrix} \le \delta(x)=\delta $$)

接下来给出有效数字的定义
如果近似值的误差界是某一位的半个单位，且该位到近似值的第一位有n个非零数，那么该近似值就有n位有效数字

使用四舍五入法可以使绝对误差最小，并且利用四舍五入法来计算近似值，每一位数值都是有效可靠的

可进一步探寻近似值和相对误差之间的某种联系,记
通过简单的放缩可得
 \times 10^{m-1}$$)
那么当近似值的有效数字为n时，相对误差的上界为
 \end{vmatrix}= \begin{vmatrix} \frac{e(x)}{\tilde x} \end{vmatrix}=\begin{vmatrix} \frac{x-\tilde x}{\tilde x} \end{vmatrix} \le \frac{0.5 \times 10^{m-n}}{a_1 \times 10^{m-1} }=\frac{1}{2a_1}\times 10^{1-n}$$)

由此可以引申出一个定理
如果x的有效数字位数为n，则有 
反之，如果}\times 10^{1-n}),则有效数字位数至少有n

讨论一下函数的误差
其中绝对误差为

相对误差为
=\frac{e(y)}{\tilde y}=\frac{f^ (\tilde x)e(x)}{\tilde y} =\frac{\tilde xf^(\tilde x)e(x)}{\tilde y \tilde x}=\frac{\tilde x f^ (\tilde x)}{\tilde y}\epsilon (x)$$) 相对误差界为 ![](http://www.forkosh.com/mathtex.cgi?$$\begin{vmatrix}\epsilon(y)\end{vmatrix}\le\frac{\begin{vmatrix}\tilde x \end{vmatrix}\begin{vmatrix}f^(\tilde x)\end{vmatrix}}{\begin{vmatrix}\tilde y\end{vmatrix}}\delta(x)$$)
从而
=\frac{\begin{vmatrix}\tilde x \end{vmatrix}\begin{vmatrix}f^ (\tilde x)\end{vmatrix}}{\begin{vmatrix}\tilde y\end{vmatrix}}\delta(x) = A_{f}\delta(x)$$) ![](http://www.forkosh.com/mathtex.cgi?$A_{f}$)即函数的相对误差界放大系数 ![](http://www.forkosh.com/mathtex.cgi?$$A_{f}=\frac{\begin{vmatrix}\tilde x \end{vmatrix}\begin{vmatrix}f^(\tilde x)\end{vmatrix}}{\begin{vmatrix}\tilde y\end{vmatrix}}$$)

进一步推广至多元函数
利用Tayor展开可知其中绝对误差为

给出绝对误差界

得相对误差界

即多元函数的相对误差界放大系数

接下来介绍减少误差的计算法则

• 避免两相近数做减法
• 避免大数吃掉小数
• 避免除数过小
• 简化运算，避免重复运算

关于数值稳定的定义

如果一个算法经过多次计算，将初始的误差变大了，陈该算法为数值不稳定的，反之为数值稳定的

关于病态问题的定义

如果一个数值问题，对输入做出轻微的扰动会对输出产生较大的影响，称该问题为病态的

4.算法性态分析概述

一个算法的复杂度有两种，分别为

• 时间复杂度（指需要的计算机的时间资源）
• 空间复杂度（指需要的计算机的储存器资源）

计算复杂度取决于被求解问题的规模大小，输入数据和算法本身，计算复杂度用算法的基本运算次数与基本操作量来测量

数学上用时间复杂度为问题规模的多项式函数或者指数函数来作为区分算法好与坏的分水岭，如果时间复杂度为问题规模的多项式函数那么这个算法是好的，而如果是指数函数则被称为不好的算法

由于输入数据的不同，时间复杂度也不同，我们引入复杂度的期望作为平均时间复杂度

我们利用算法复杂度来度量那些使用直接法的算法，对于迭代的算法我们使用收敛率来评价

由于这里没有对向量，矩阵等给出其大小的“测度”，故先讨论下迭代法产生的实数的序列
收敛率的高低使用收敛阶的大小衡量

Def:如果上述实数序列收敛于x，即，假定存在某个正数,使得极限
![](http://www.forkosh.com/mathtex.cgi?$$
\lim_{k\to \infty}\frac{e_{k+1}}{e_k^r}=\lim_{k\to \infty}\frac{\begin{vmatrix} x_{k+1}-x\end{vmatrix}}{\begin{vmatrix} x_{k}-x\end{vmatrix}^r}=c_r>0$$)
存在，称该迭代法是r阶收敛

• r=1时为线性收敛
• r>1时为超线性收敛
  • r=2，平方收敛
  • r=3，立方收敛

需要注意的是，若有
也称为超线性收敛
收敛阶如果比较小，则需要加速，这是数值计算的重要研究课题